CF 1956 C. Nene's Magical Matrix (*1600) 构造

CF 1956 C. Nene's Magical Matrix (*1600) 构造

题目链接

题意：

给你一个 \(n\times n\) 的矩阵，你现在有两个操作，可以将一行或者一列全部赋值为一个大小为 \(n\) 的排列。构造使得矩阵和最大的方案。

思路：

观察样例，手玩一下，发现他们一定构造成下面这样是最大值的情况。操作次数是 \(2\times n-1\) 次。

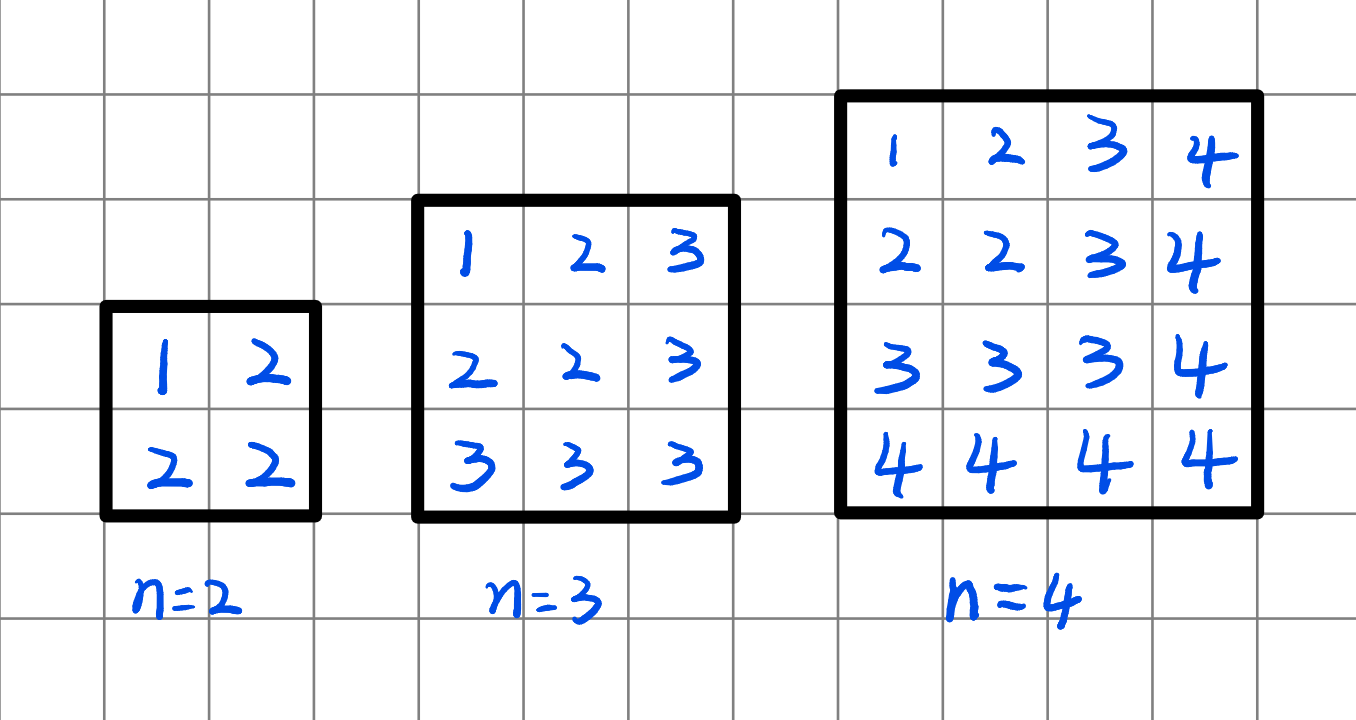
考虑如何构造，因为我们发现后面的值会覆盖前面的值，观察发现，我们只需要先构造一行在构造一列，并且从后往前从下往上构造即可。

代码：

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'
#define debug(x) cout<<#x<<":"<<x<<endl;

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;
const int cases = 1;

void Showball(){
   int n;
   cin>>n;
   int t=n;
   int ans=0,cur=1;
   for(int i=1;i<=n;i++){
   	 ans+=cur*i;
   	 cur+=2;
   }
   cout<<ans<<" "<<2*n-1<<endl;
   for(int i=1;i<=2*n-1;i++){
   	  if(i&1){
   	  	cout<<1<<" "<<t<<" ";
   	  	for(int j=1;j<=n;j++) cout<<j<<" \n"[j==n];
   	  	t--;
   	  }else{
   	  	cout<<2<<" "<<t<<" ";
   	  	for(int j=1;j<=n;j++) cout<<j<<" \n"[j==n];
   	  }
   } 
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T=1;
    if(cases) cin>>T;
    while(T--)
    Showball();
    return 0;
}