machine learning[GMM-EM]
介绍下EM算法和GMM模型,先简单介绍GMM的物理意义,然后给出最直接的迭代过程;然后再介绍EM。
1 高斯混合模型
高斯分布,是统计学中的模型,其输出值表示当前输入数据样本(一维标量,多维向量)的概率。
1.1 多元高斯分布
如高斯分布-笔记所述,多元高斯函数公式为:
其中\({\bf x}=[x_1,x_2,...,x_d]^T\)是\(d\)维的列向量;
\({\bf \mu}=[\mu_1,\mu_2,...,\mu_d]^T\)是\(d\)维均值的列向量;
\(\Sigma\)是\(d\times d\)维的协方差矩阵;
\({\Sigma}^{-1}\)是\(\Sigma\)的逆矩阵;
\(|\Sigma|\)是\(\Sigma\)的行列式;
\((\bf x-\mu)^T\)是\((\bf x-\mu)\)的转置,且
其中\(\mu,\Sigma\)分别是向量\(\bf x\)和矩阵\((\bf x -\mu)(\bf x -\mu)^T\)的期望。
1.1 高斯混合模型定义
如图所示,假定我们当前的样本都是2维特征的样本,即表现在特征空间中就是在2维坐标系上有多个数据点
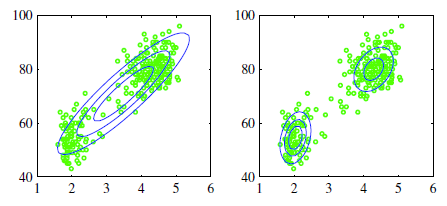
图1.1.1 二维空间中的数据样本下,用一个高斯分布去拟合,或者2个高斯分布模型去拟合
从左图可看出,通过一个高斯模型去拟合,总觉得很违和,因为所谓的高斯分布是中间密集,然后随着距离越远则越稀疏,即密集和稀疏程度就表示着当前出现样本点的概率,如
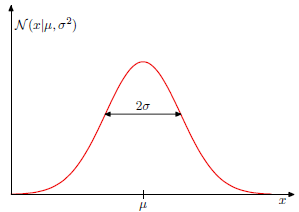
图1.1.2 一维高斯图形,其中x轴表示输入值,y轴表示概率值

图 1.1.3二维高斯分布呈现,乃至球面高斯分布图形。
ps: 在最后一个图形中,z轴表示当前出现样本的概率,可以看出越靠近中心,样本出现的概率越大,而越远离,则样本出现的概率越小
回头看图1.1.1,可以得出,如果是这种数据,是不合适用单一高斯分布去拟合的。
接下来我们看看两个例子:
- 假设paperback书籍的售价是服从均值为10.00,标准差为1.00的高斯分布;而hardback 书籍的售价服从均值为17,方差为1.5的高斯分布。那么随便挑一本书,其价格是服从单一高斯分布么?
结果肯定是否。直观来说,单一高斯分布是中间密度大,而离中间越远则密度会快速下降就像单一山峰,但是这里随便挑一本的价格却是服从双峰的。这里分布的中心的售价大约是13,而找到13块钱的一本书的概率却远低于10或者17的周边。- 另一个例子:略
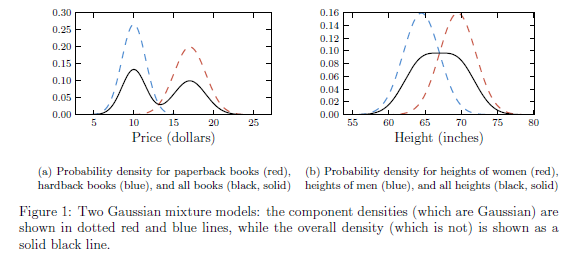
图1.1.4 一维数据下的高斯混合模型的两个例子
这里我们先简单拿出高斯混合模型的公式:
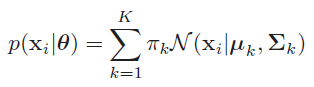
如公式所述,所谓多维高斯分布,就是多个高斯分布的线性组合,也就是通过将多个高斯分布乘以对应的权重来完成样本数据的拟合。在这其中
\(0 \leq \pi_k \geq 1\),且\(\sum{\pi_k} =1\)
即,这里表达的物理意义是:
- 在多维特征空间中,每一个样本是基于多个高斯分布而生成的,比如基于当前\(\theta\)基础上,\(p(x_i| \theta)=0.5*G1+0.3*G2+0.2*G1\)
意思就是该样本点50%概率来自高斯1分布,30%概率来自高斯2分布,20%概率来自高斯3分布。
上面介绍的都是2个高斯分布的情况,如下图,假设我们引入三个高斯分布
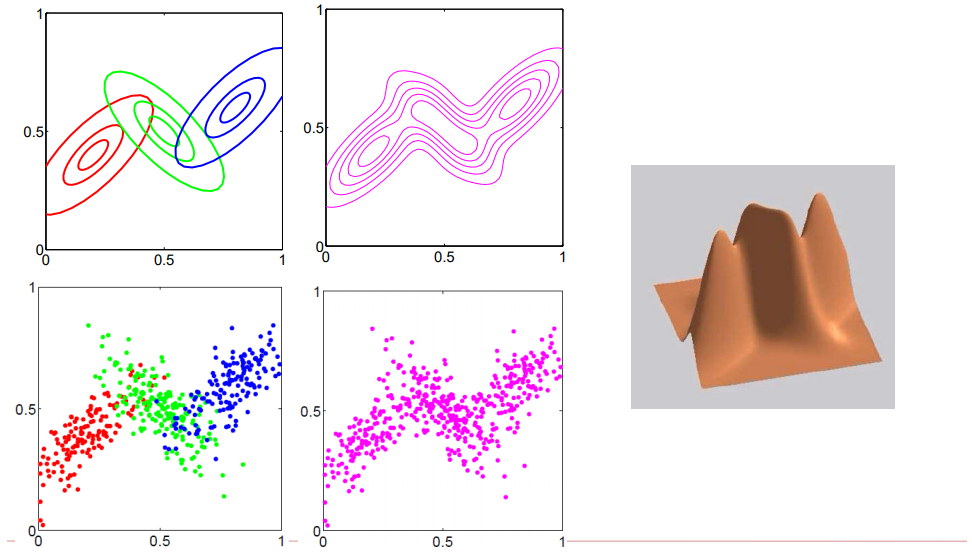
图1.1.5 三个高斯分布在2维空间中的展示
如上图所述,我们拿到的样本集合自然都是一些在特征空间中的点,所谓用混合高斯模型去拟合,也就是为了求得每个样本点来自对应的高斯分布的概率(\(\pi_k\))以及每个高斯分布的参数(均值和方差)。可以自然推广出,只要参与的高斯分布越多,那么就能表示越多的样本点,那么只要足够多的高斯分布进行线性组合,那么就能拟合整个特征维度的空间中表示的样本。
1.2 求每个样本属于不同高斯分布的概率
如1.1中混合高斯的公式
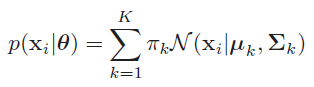
我们将其简写成
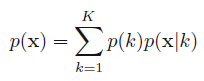
这里表示的就是每个样本的概率来自所有基于选定第\(k\)个高斯分布基础上该高斯分布的概率之和。那么对应的后验概率\(p(k|\mathbf{x})\)我们表示成\(\gamma_k( \mathbf{x} )\):
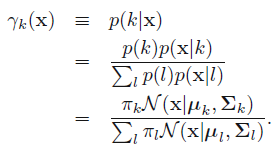
对应的含义:
- 基于当前参数集合固定的基础上,给定一个样本,该样本来自第k个高斯分布的概率,从而完成了先混合高斯聚类,然后进行简单分类的过程。
1.3 用EM进行估计GMM的参数的直接过程
GMM模型如上述解释的,现在,我们关注点就到了如何去用GMM拟合样本集,也就是训练过程。这其中,K是需要预先人为指定的,就和K-means一样。那么在指定了K之后,整个GMM模型的参数一共为\(\pi,\mu,\Sigma\).而通常用来训练GMM的算法叫做EM算法,也就是(expectation maximization,EM) (Dempster et al. 1977; Meng and van Dyk 1997; McLachlan and Krishnan 1997)。下面会详细介绍EM算法,而这里为了简洁,就直接给出基于EM算法的GMM求解过程:
众所周知,EM包含了两个阶段:
- E阶段:求期望函数;
- M阶段:对期望函数最大化。
在这其中,我们需要计算最大似然估计,也就是,假设我们有\(N\)个样本,每个样本表示为\(\mathbf{x}_i\),且假设有\(K\)个高斯分布,则对应的最大似然估计就是
左右取对数得:
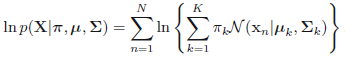
而对于GMM模型来说,对应的阶段为:
- 初始化阶段:先随机初始化\(\pi, \mu, \Sigma\) 。
- E阶段:使用当前的参数,基于每个样本计算各自的高斯响应值(就是之前介绍的后验概率\(p(k|\mathbf{x})\))
ps:一共\(N\)个样本,每个样本都有\(K\)次计算,则当前E阶段一共需要计算\(N \times K\)次- M阶段:更新参数,基于所有样本,计算各自对应的高斯参数。我们可以想象这样一个网格,其中行表示\(N\)个样本数量,列表示\(K\)个高斯模型,则E阶段是计算网格所有的部分,而M阶段是按照列,每次计算一列中\(N\)个值的均值,要计算\(K\)个模型次数。
这里
- 评估阶段:计算log似然
并观察log似然和参数\(\pi, \mu, \Sigma\) 是否收敛,如果收敛则停止迭代,否则,接着计算E阶段和M阶段。
从上面可以看出,基于EM的GMM计算需要的计算量有些大,故而如果样本量较多,该方法一次迭代所需要的计算次数就很多。
2 EM算法
上面基于GMM给出了最终的简洁结果,这里我们详细介绍下EM的原理及概念。值得注意的是,EM算法对初始值十分敏感,且容易陷入局部最优。
2.1 EM通用计算流程
通常在ML中,给的数据无外乎样本和标签,如果我们采用的模型是直接基于这些计算的,那么就很容易了,比如k-means。而如果采用的模型是包含了隐含变量的,那么对于整个算法来说,就还需要考虑到缺失的数据信息。也就是所谓的潜在变量。例如:
- 李航书里面介绍的例子:有三个硬币A,B,C。我们先抛掷硬币A,如果朝上则抛掷硬币B,否则抛掷硬币C。然后将硬币B或者C的结果进行收集,当作观测结果,那么假设一共收集了十个[1,1,0,1,0,0,1,0,1,1]。可是我们并不知道每次结果是来自B还是来自C,其中包含着硬币A的未观测数据。所以我们将观测的结果视为观测变量,而硬币A视为潜在变量。
- GMM模型:给定一个样本集合,其中每个样本点是观测到的数据,而该数据来自哪个高斯分布是潜在变量(虽然\(\pi_k\)表示概率,可是我们如果取最大概率的为生成该样本的高斯分布,则可以将其视为one-hot形式)
EM算法就是一个迭代算法,通过E计算潜在变量的期望值;并在M阶段基于潜在变量期望值去计算其他模型变量的期望值。
我们假设所有的观测数据为\(\mathbf{X}=\{\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,...,\mathbf{x}_N\}\),其中,该模型包含潜在变量\(\mathbf{Z}=\{\mathbf{z}_1,\mathbf{z}_2,\mathbf{z}_3,...,\mathbf{z}_M\}\),并假设所有的模型参数为\(\theta\),那么该模型的log似然函数为:
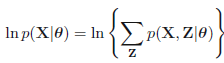
等效于下面式子
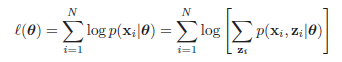
其中\(\mathbf{x}_i\)表示在数据集中第\(i\)个观测样本,\(\mathbf{z}_i\)表示该观测样本下涉及的潜在变量,上式子中\(p(\mathbf{x}_i|\theta)=\sum_{\mathbf{z}_i} p(\mathbf{x}_i,\mathbf{z}_i|\theta)\),即边缘分布。
从上面式子可以看出log无法更进一步的塞到求和操作里面,而是先求和然后在log,然后再求和,这就导致计算十分困难。这里我们将\(\{\mathbf{X},\mathbf{Z}\}\)称为完全数据,而将\(\mathbf{X}\)称为不完全数据 。然而基于不完全数据基础上,我们需要进行模型的参数迭代,所以我们先要基于\(\theta^{old}\)计算\(p(\mathbf{Z}|\mathbf{X},\theta^{old})\),然后计算\(\theta^{new}\).
这里一个重要函数\(Q(\theta,\theta^{old})\)(在M阶段需要用到),其是基于给定观测数据\(\mathbf{X}\)和当前参数\(\theta^{old}\)基础上,对未观测数据\(\mathbf{Z}\)的条件概率分布\(p(\mathbf{Z}|\mathbf{X},\theta^{old})\)的期望(李航的观点).也可以理解成基于给定观测数据和当前参数基础上对完全数据的期望(mlapp观点)。其中完全数据的极大似然log函数为\(\log p(\mathbf{Z},\mathbf{X}|\theta)\)
ps:上式是示意式子,具体的过程可以看基于GMM的EM过程更具体的了解这部分的变化。
通用EM流程为:
- 初始化:先初始化参数\(\theta^{old}\)
- E阶段:计算\(p(\mathbf{Z}|\mathbf{X},\theta^{old})\)
- M阶段:计算\(\theta^{new}=\underset{\theta}{argmax}Q(\theta,\theta^{old})\)
这里\(Q(\theta,\theta^{old})=\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\theta^{old})\log p(\mathbf{X},\mathbf{Z}|\theta)\),所谓最大化也就是最大化\(\sum_{\mathbf{Z}}log p(\mathbf{X},\mathbf{Z}|\theta)\)这部分,即基于当前参数的完全数据的期望- 评估阶段:检查当前log似然函数和参数是否收敛,更换参数:\(\theta^{old}=\theta^{new}\)
如果收敛则停止迭代,否则接着循环E阶段和M阶段
2.2 基于GMM的EM计算过程
这里我们重新回头看GMM是如何用EM来求解的。
首先,假设观测数据\({\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_N}\)是由高速混合模型生成的:
其中,\(\theta={\pi_1,\pi_2,...\pi_K;\theta_1,\theta_2,...\theta_K}\)。
1 先明确潜在变量,写出完全数据的对数似然函数
这里假设观测数据\(\mathbf{x}_i\)是这样产生的:首先按照概率\(\pi_k\)选择第k个高斯分布,然后根据该高斯分布生成该观测数据。这时候,观测数据\(\mathbf{x}_i\)是已知的,而该观测数据来自哪个分布是未知的,我们假设为\(\gamma_{jk}\),表示第\(j\)个样本关于第\(k\)个高斯分布的选择:
其中\(\gamma_{jk}\)是个\({0,1}\)二值变量。
此时 基于每个样本的完全数据是\((\mathbf{x}_j,\gamma_{j1},\gamma_{j2},...,\gamma_{jK})\),其中\(j=1,2,...,N\)
则对应的完全数据的似然函数为:
其中,\(n_k=\sum_{j=1}^N\gamma_{jk}\),\(\sum_{k=1}^Kn_k=N\)
则,完全数据的对数似然函数为:
2 E阶段,确定Q函数
ps:最后一个式子,就等于2.1部分的表现形式\(\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\theta^{old})\log p(\mathbf{X},\mathbf{Z}|\theta)\)
可以看到,对整个完全数据的期望,最后就需要求解关于潜在变量的期望,这里只需要计算\(E(\gamma_{jk}|\mathbf{X},\theta)\),这里记为\(\hat \gamma_{jk}\)
则
其中\(j=1,2,...,N;k=1,2,...K\)。
将\(\hat \gamma_{jk}=E(\gamma_{jk}|\mathbf{X},\theta)\)和\(n_k=\sum_{j=1}^NE\hat \gamma_{jk}=\sum_{j=1}^N\gamma_{jk}\)带入得:
ps:值得注意的是,上面式子中的中括号部分,可以替换成任意其他分模型,不一定是高斯模型
3 确定M阶段
M阶段就是为了求\(Q(\theta,\theta^{old})\)的关于\(\theta\)的极大值,即:
这里用\(\hat \mu_k\),\(\hat \sigma_k^2\),\(\hat \alpha_k\),\(k=1,2,3,...,K\)表示\(\theta^{new}\)中的各参数,求\(\hat \mu_k\),\(\hat \sigma_k^2\)只需要将\(Q(\theta,\theta^{old})\)求偏导数,然后等于0,求出其值即可,而在求\(\hat \alpha_k\)时,因为有约束条件\(\sum_{k=1}^K\alpha_k=1\),所以需要用拉格朗日乘子法求偏导。
令其等于0,并左右乘以\(\Sigma_k^{-1}\)(我们假设该协方差矩阵是非奇异的)。则\(\sum_{j=1}^N\hat \gamma_{jk}\mathbf{x}_j=\sum_{j=1}^N\hat \gamma_{jk}\mu_k=E\mu_k\sum_{j=1}^N\hat \gamma_{jk}\),所以
同理:
2.3 EM的证明过程 李航
参考文献:
- 高斯分布-笔记
- Gaussian mixture models and the EM algorithm
- gmm
- Pattern.Recognition.and.Machine.Learning,.Christopher.M..Bishop,.Springer,.2006
- Machine learning a probabilistic perspective
- 李航统计学习方法
- 高斯混合模型(GMM)及其EM算法的理解
- matrix_cookbook
- Matrix_calculus



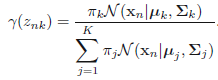
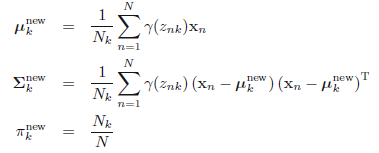

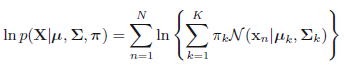

 浙公网安备 33010602011771号
浙公网安备 33010602011771号