face recognition[variations of softmax][L-Softmax]
本文来自《Large-Margin Softmax Loss for Convolutional Neural Networks》,时间线为2016年12月,是北大和CMU的作品。
0 引言
过去十几年,CNN被应用在各个领域。大家设计的结构,基本都包含卷积层和池化层,可以将局部特征转换成全局特征,并具有很强的视觉表征能力。在面对更复杂的数据下,结构也变得更深(VGG),更小的strides(VGG),新的非线性激活函数(ReLU)。同时受益于很强的学习能力,CNN同样需要面对过拟合的问题。所以一些如大规模的训练集,dropout,数据增强,正则,随机池化等都不断被提出。
最近的主流方向倾向于让CNN能够学到更具辨识性的特征。直观上来说,如果特征具有可分性且同时具有辨识性,这是极好的。可是因为许多任务中本身包含较大的类内变化,所以这样的特征也不是轻易能够学到的。不过CNN强大的表征能力可以学到该方向上的不变性特征,受到这样的启发,contrastive loss和triplet loss都因此提出来增强类内紧凑性和类间可分性。然而,一个后续问题是,所需要的图片二元组或者三元组理论上需要的量是\(O(N^2)\),这里\(N\)是训练样本的个数。考虑到CNN经常处理大规模训练集合,所以需要精心的选择训练集的一个子集来拟合这些loss函数。因为softmax的简洁和概率可解释性,softmax被广泛的应用。再加入cross-entropy loss一起使用,形成了最CNN分类结构中最常用的组件。
本文中,作者将softmax loss定义为cross-entropy loss,softmax函数和最后一层全连接层的组合。如下图

基于这样的设定,许多流行的CNN模型可以被看成一个卷积特征学习组件和一个softmax loss组件的组合。可是之前的softmax loss不能显式的推进类内紧凑和类间可分。作者一个直观观点是模型的参数和样本可以因式分解成幅度和具有cos的相似性角度:
这里\(c\)是类别索引,对应的最后全连接层参数\(\mathbf{W}_c\)可以看成是关于类\(c\)的线性分类器的参数。基于softmax loss,标签预测决策规则很大程度上是被每个类别的角度相似度决定的(因为softmax loss使用余弦距离作为分类得分)。
作者本文的目的就是通过角度相似度项,泛化softmax loss到一个更通用的大边际softmax(L-Softmax)loss上,从而让学到的特征之间具有更大的角度可分性。通过预设常数\(m\),乘以样本和ground-truth类别分类器之间的角度。\(m\)确定了靠近ground-truth类的强度,提供了一个角度边际。而传统的softmax loss可以看成是L-sofmax loss的一个特例。
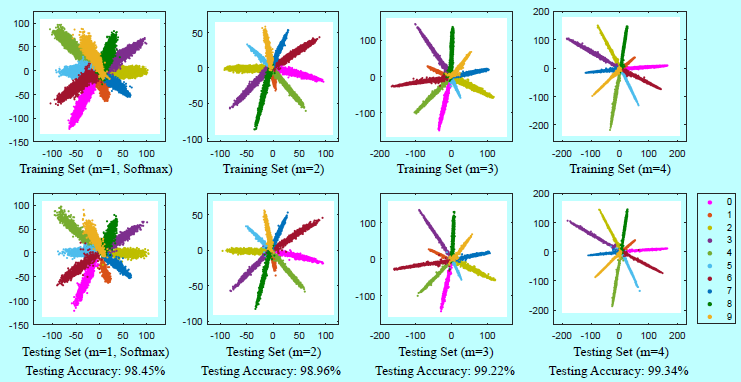

如上图可以看出,L-Softmax学到的特征可以变得更紧凑和更可分。
L-Softmax loss是一个灵活的可以调整类内角度边际限制的目标函数。它提出了可调节难度的学习任务,其中随着所需边际变大,难度逐渐增加。L-Softmax loss有好几个优势:
- 倾向扩大类之间的角度决策边际,生成更多辨识性的特征。它的几何解释也十分清晰和直观;
- 通过定义一个更困难的学习目标来部分避免过拟合,即采用了不同的观点来阐述过拟合;
- L-Softmax不止得益于分类问题。在验证问题中,最小的类间距离也会大于最大的类内距离。这种情况下,学习可分性的特征可以明显的提升性能。
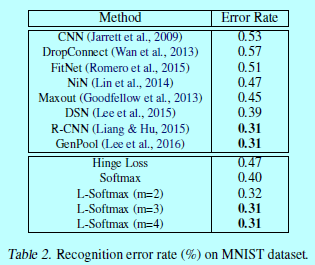
作者的实验验证了L-Softmax可以有效的加速分类和验证任务的性能。更直观的,图2和图5中的特征可视化都揭示了L-Softmax loss更好的辨识性
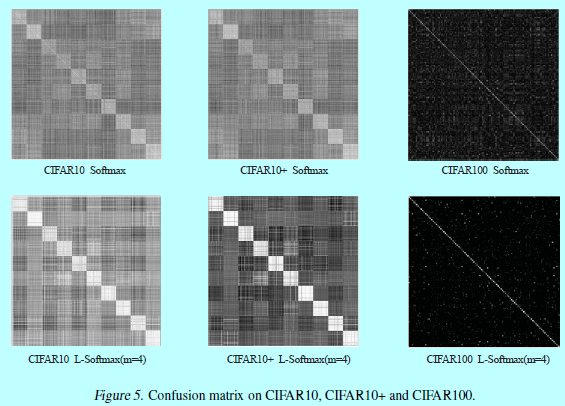
作为一个直观的softmax loss泛化,L-softmax loss不止是继承了所有softmax loss的优点,同时让特征体现不同类别之间大角度边际特性。
1 Softmax Loss以cos方式呈现
当前广泛使用的数据loss函数包含欧式loss,hinge(平方) loss,信息增益loss,contrastive loss, triplet loss, softmax loss等等。为了增强类内紧凑性和类间可分性,《Deep learning face representation by joint identificationverification》提出将softmax和contrastive相结合。contrastive loss输入的是一对训练样本,如果这对样本属于同一个类,那么contrastive loss需要他们的特征尽可能的相似;否则,contrastive loss会让他们的距离超过一个边际阈值。
而不管是contrastive loss还是triplet loss都需要仔细的设计样本选择过程。而他们都更加倾向类内紧凑性和类间可分性,这也给作者一些灵感:在原始softmax loss上增加一个边际限制。
作者提出在原始softmax loss上进行泛化。假设第\(i\)个输入特征\(x_i\)和对应的label是\(y_i\)。那么原始softmax loss可以写成:
其中,\(f_j\)表示类别得分\(\mathbf{f}\)向量的第\(j\)个元素(\(j\in [1,K]\),K表示类别个数),N表示样本个数。在softmax loss中,\(\mathbf{f}\)通常表示全连接层\(\mathbf{W}\)的激活函数,所以\(f_{y_i}\)可以写成\(f_{y_i}=\mathbf{W}_{y_i}^Tx_i\),这里\(\mathbf{W}_{y_i}\)是\(\mathbf{W}\)的第\(y_i\)列。注意到,忽略了\(f_j\)中的常量\(b\),\(\forall j\)为了简化分析,但是L-Softmax loss仍然可以容易的修改成带有\(b\)的(性能没什么差别)。
因为\(f_j\)是基于\(\mathbf{W}_j\)和\(x_i\)的内积,可以写成\(f_j=||\mathbf{W}_j||||x_i||cos(\theta_j)\),这里\(\theta_j(0\leq \theta_j \leq \pi)\)是基于\(\mathbf{W}_j\)和\(x_i\)向量的夹角,因此loss变成:
2 Large-Margin Softmax Loss
2.1 直观
这里先给出一个简单的例子来直观的描述一下。考虑一个二分类问题,有一个来自类别1的样本\(x\),为了正确分类,原始softmax表现为\(\mathbf{W}_1^Tx> \mathbf{W}_2^Tx\)(即,\(||\mathbf{W}_1||||x||cos(\theta_1)> ||\mathbf{W}_2||||x||cos(\theta_2)\))。然而,为了生成一个决策边际而让分类更严格,作者认为可以\(||\mathbf{W}_1||||x||cos(m\theta_1)>||\mathbf{W}_2||||x||cos(\theta_2)(0 \leq \theta_1 \leq \frac{\pi}{m})\),这里\(m\)是一个正整数,因为有下面不等式:
因此,\(||\mathbf{W}_1||||x||cos(\theta_1) > ||\mathbf{W}_2||||x||cos(\theta_2)\).所以新分类标准是一个更强的标准。
2.2 定义
按照上面的解释,L-Softmax loss定义为:
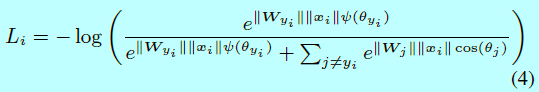
其中定义为:
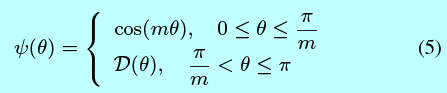
这里\(m\)是一个整数,与分类边际密切相关。当\(m\)变得更大时,分类边际也更大,学习的目标同时也变得更难。同时\(\mathcal{D}(\theta)\)是一个单调递减的函数,\(\mathcal{D}(\frac{\pi}{m})\)等于\(cos(\frac{\pi}{m})\)

为了简化前向和后向传播,本文中作者构建了一个特殊的函数\(\psi (\theta_i)\):
这里\(k\in[0, m-1]\),\(k\)是一个整数。将式子1,式子4,式子6相结合,得到的L-Softmax loss。对于前向和后向传播,需要将\(cos(\theta_j)\)替换为\(\frac{\mathbf{W}_j^Tx_i}{||\mathbf{W}_j||||x_i||}\),然后将\(cos(m \theta_{y_i})\)替换成:
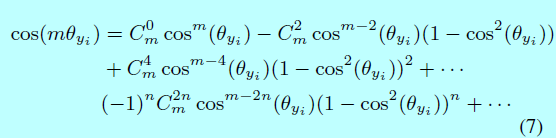
这里n是整数且\(2n \leq m\)。在消掉\(\theta\)之后,可以求关于\(x\)和\(\mathbf{W}\)的偏导。
2.3 几何解释
作者的目标是通过L-Softmax loss来得到一个角度边际。为了简化几何上的解释,这里分析二分类情况,其中只有\(\mathbf{W}_1\)和\(\mathbf{W}_2\)。
首先,假设\(||\mathbf{W}_1||=||\mathbf{W}_2||\),如图4。
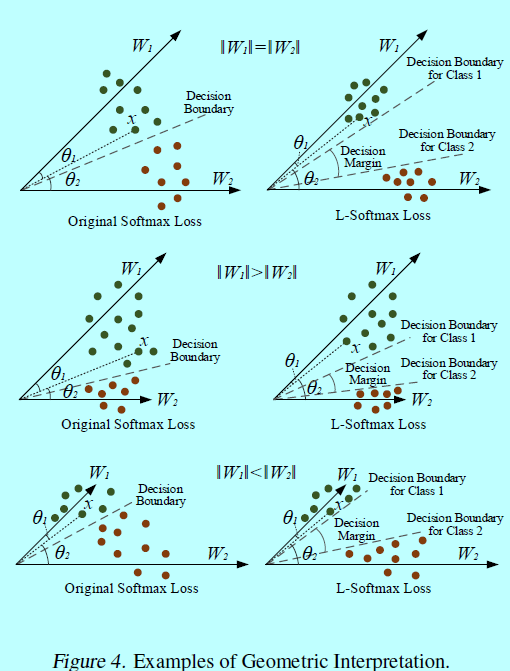
当\(||\mathbf{W}_1||=||\mathbf{W}_2||\)时,分类结果完全依赖介于\(x\)和\(\mathbf{W}_1(\mathbf{W}_2)\)。在训练阶段,原始的softmax需要\(\theta_1<\theta_2\)去将样本\(x\)分为1类,同时,L-Softmax loss需要\(m\theta_1<\theta_2\)来保证同样的决策。可以发现L-Softmax是更严格的分类标准,从而生成一个介于类1和类2分类边际。假设softmax和L-Softmax都优化到相同的值,然后所有的训练特征可以十分完美的分类,那么,介于类1和类2之间的角度边际可以通过\(\frac{m-1}{m+1}\theta_{1,2}\)得出,这里\(\theta_{1,2}\)是基于向量\(\mathbf{W}_1\)和\(\mathbf{W}_2\)之间的角度。L-Softmax loss同样也会建立类1和类2的决策面。从另一个角度,让\(\theta_1^{'}=m\theta_1\),并假设原始softmax和L-Softmax可以优化到相同的值。那么可以知道在原始softmax中\(\theta_1^{'}\)是L-Softmax中\(\theta_1\)的m-1倍。所以介于学到的特征和\(\mathbf{W}_1\)之间的角度会变得更小。对于每个类别,都有相同的结论。本质上,L-Softmax 会缩小每个类可行的角度,并在这些类上生成 一个边际。
对于\(||\mathbf{W}_1||>||\mathbf{W}_2||\)和\(||\mathbf{W}_1||<||\mathbf{W}_2||\)等情况,几何解释更复杂一些。因为\(\mathbf{W}_1\)和\(\mathbf{W}_2\)的模是不同的,类1和类2的可行角度也是不同的。正常的更大的\(\mathbf{W}_j\),对应的类就有更大的可行角度。所以,L-Softmax loss会对不同的类生成不同角度的边际。同时也会对不同的类生成不同的边际。
2.4 讨论
L-Softmax loss在原始softmax上做了一个简单的修改,在类之间获得了一个分类角度边际。通过设定不同的m值,就定义了一个可调整难度的CNN模型。L-Softmax loss有许多不错的特性:
- L-Softmax 有一个清晰的几何解释。m控制着类别之间的边际。更大的m(在相同训练loss下),表示类别之间理想的边际也更大,同时学习的困难程度也会上升。当m=1,L-Softmax就是原始softmax;
- L-Softmax 定义了一个带有可调整边际(困难)的学习目标。一个困难的学习目标可以有效的避免过拟合,同时继承深度和广度结构上很强的学习能力;
- L-Softmax 可以很容易的作为标准loss的一个选择,就和其他标准loss一样,也包含可学习的激活函数,数据增强,池化函数或其他网络结构模型。
3 优化
L-Softmax loss的前向和后向是很容易计算的,所以也很容易通过SGD进行迭代优化。对于\(L_i\),原始softmax和L-Softmax之间的差别在于\(f_{y_i}\)。因此只需要在前向和后向中计算\(f_{y_i}\),且同时其他的\(f_j,\, j \neq y_i\)与原始softmax是一样的,将式子6和式子7相结合,得到\(f_{y_i}\):

其中:

且,k是一个整数,取值为\([0,m-1]\)。对于后向传播,使用链式法则去计算偏导
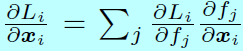 和
和 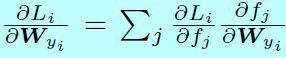
因为\(\frac{\partial L_i}{\partial f_j}\)和\(\frac{\partial f_j}{\partial x_i},\, \frac{\partial f_j}{\mathbf{W}_{y_i}},\forall j \neq y_i\)在原始softmax和L-Softmax都是一样的,所以为了简洁,\(\frac{\partial f_{y_i}}{\partial x_i}\)和\(\frac{\partial f_{y_i}}{\partial \mathbf{W}_{y_i}}\)可以通过下面式子计算:
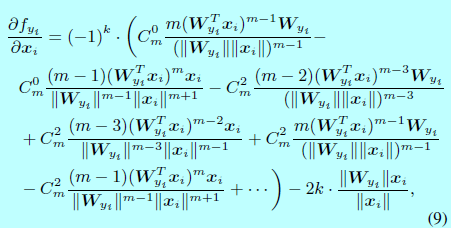
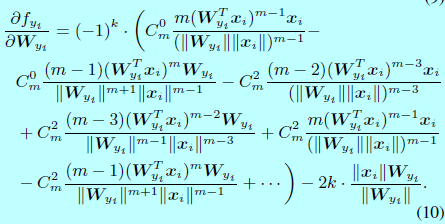
在实现过程中,k可以通过构建一个关于\(\frac{\mathbf{W}_{y_i}^Tx_i}{||\mathbf{W}_{y_i}||||x_i||}\)(即\(cos(\theta_{y_i})\))的查找表。举个例子,给定一个m=2时候的力气,此时\(f_i\)写成:
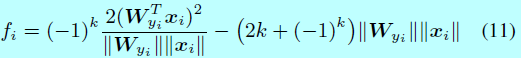
其中:
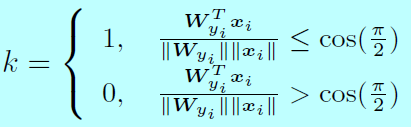
在后向传播中,\(\frac{\partial f_{y_i}}{\partial x_i}\)和\(\frac{\partial f_{y_i}}{\partial \mathbf{W}_{y_i}}\)计算为:
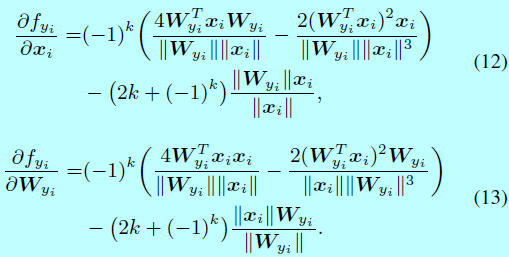
当\(m\geq 3\)时,仍然可以通过式子8,式子9,式子10来计算前向和后向。
4 实验细节
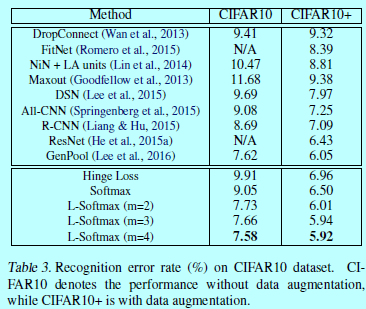
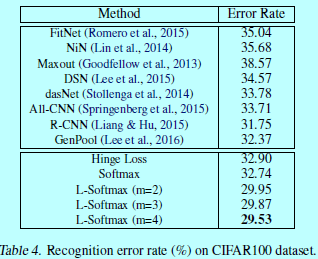
在两个类型数据集上进行了本文方法的测试:图像分类和人脸验证。在图像分类中使用MNIST,CIFAR10,CIFAR100;在人脸验证中使用LFW。只有在softmax层有差别,前面的网络结构在每个数据集上都是各自一样的。如下图
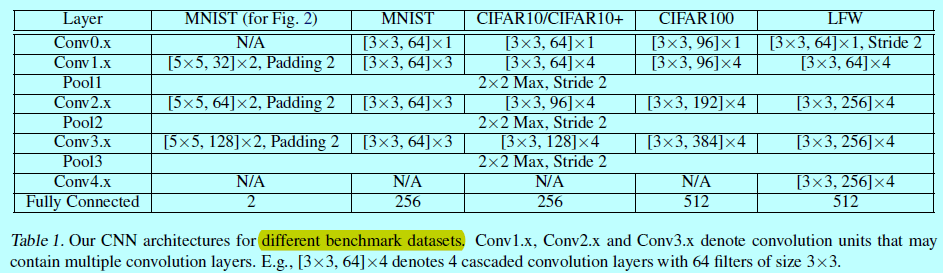
网络结构上,略
当训练具有较多目标的数据集如CASIA-WebFace上,L-Softmax的收敛会变得比softmax 要困难,对于这种情况,L-Softmax就更难收敛,这时候的学习策略是
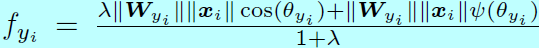
且梯度下降开始时采用较大值的\(\lambda\)(接近原始softmax),然后逐步的减小\(\lambda\),理想情况下\(\lambda\)会减少到0,不过实际情况中,一个较小的值就能满足了。

。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号