二分查找详解

大佬原文链接：二分查找从入门到入睡

简介

二分查找是一种简单高效的查找算法，通常用于在有序或二段性(后有详解)的数组中查找某个元素。其基本原理是每次与数组中间元素进行比较，可以缩小一半的查找空间，直到找到目标元素或者区间被缩小为0，目标不存在。二分查找以其原理极为简单，但细节处理却极易出错而闻名。

• 时间复杂度：O(logn)，其中 n 是数组的长度。
• 空间复杂度：O(1)。

可能提出的疑问

尽管二分查找的基本思想相对简单，但细节可以令人难以招架 ... — 高德纳

不同情况用哪种符号

• 左右边界初始值为何有时候是 n, 有时候是 n - 1?
• while中的条件什么时候用 <，什么时候用 <= ?
• 左右界更新条件的不等号该写哪一个 <, <=, >, >= ?
• 左右界更新语句该写哪一个 l = c + 1 / l = c / r = c - 1 / r = c ？
• 中间值下标为什么写成 l + (r - l) / 2 ？
• 返回值到底是 l 还是 r 还是 l - 1, l + 1, r - 1, r + 1...？

千万别死记硬背，理解【循环不变】原则后可以轻松写出。

为什么会无限循环

错误示例(以模板二情形3为例)：

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n
    while l<r:
        c=l+(r-l)//2
        if nums[c]<=target:
            l=c
        else:
            r=c+1
    #return r-1 if (nums[r]==target) else -1 # 处理相等返回情形
    return l if r!=-1 else -1

该代码意外地陷入了无限循环，产生原因如下：

• 产生循环的条件是某一次进入while时，c = l + (r - l) // 2，使得 nums[c] <= target，于是进入 if 分支，l = c，且假设此次循环开始时 l = c。检视该假设的正确性，将计算 c 的式子中的 c 换成 l，有 l = (l + r) / 2。
• l + r 为偶数时，l = r，与进入while的条件矛盾，故 l = c 的假设与 l + r 为偶数互相矛盾。
• l + r 为奇数时，l = r - 1。意想不到的事情发生了，这是可能达到的一种情况。 也就是说，「情形3」代码在某一次进入while时，若 l = r -1，且nums[c] <= target时，将发生无限循环。

e.g.,对于数组 nums = {-1,0,3,5,9,12}，target = 3，以其为输入运行「情形3」代码，程序将在 l = 1, r = 2 （满足 l = r - 1，且此时nums[c] = nums[1] = 0 <= target = 3）时开始无限循环。但若target = 5，则程序正常结束，返回正确的结果（建议实际动手分析一下）。实际上只要target大于nums中所有数字，则必然发生无限循环，因为 r 不会更新， l 向 r 逐渐靠近后最终一定位于 r 的前一位，即 l = r - 1，而此时必然有 nums[c] <= target，于是会在这个时候陷入无限循环。

什么是二段性

二分查找不一定需要数组有序，只需要具备「二段性」即可。

关于「二段性」，你会看到有些题目的数组并不具备有序性，但丝毫不妨碍以二分查找处理。这是因为，只要数组能够根据特定的条件（其实就是「循环不变」）被分为两半，且搜索空间为其中的一半，循环地如此二分下去，直到穷尽原搜索空间，最终必能确定答案（存在与否，及若存在是哪个）。这就是「二段性」，更严谨点说是 「输入序列对于答案可被二分至穷尽」 这一本质特征。最典型的莫过于162. 寻找峰值 ，输入元素大小和顺序是任意的，只需至少存在一个数，其左右两边的数小于它即可。看起来十分反直觉，但仍可通过「循环不变」知道其满足上述本质特征，了解到这一点后就不会觉得有多特别了。

循环终止时l、r下标的关系是怎么确定的，为什么是确定的？

模板一的错位终止和模板二的相等终止有详细介绍及证明。

为什么会提前溢出

关于求中间值坐标的写法。
最简单的写法是 c = (l + r) / 2，但直接相加会使得 l + r 大于 2^31-1 (2147483647) 时（提前）溢出，例如 l = 1, r = 2^31-1，计算 c 时， l + r = 2^31 (2147483648) 导致溢出。但原本应该有 c = 1073741824，l, r, c都不应该溢出，只是因为 l + r 导致了（提前）溢出。
因此改写成先减后加的形式 c = l + (r - l) // 2。这是最常见的形式。
很多人会用 >> 代替除法，写成 c = l + ((r - l) >> 1) 也是可以的。
值得一提的是JDK中采用的是 c = (l + r) >>> 1的写法。

• ">>>" 是无符号右移运算符(Unsigned right shift operator)，与 >> 的区别在于右移的时不考虑符号位，总是从左侧补0，l + r 不溢出的时候符号位本来就是0，与 >> 效果相同。 l + r 溢出时最高位符号位从0进位成了1，经过 >>> 的移位，最高位又变回了0，这是一种利用位运算的trick，可以参考这里。
• 需要注意的是若采用此种写法，需要保证 (l + r) 为非负整数。因为若 (l + r) 为负数，经过高位补0后将得到错误的正数。通常情况下，l 与 r 代表下标，不会出现负数情况，但有的题目要在包含正负数的范围内，对这些「数值」（而非下标）进行二分查找， l 和 r 表示可能为正也可能为负的「数值」，此时就不用能 >>> 的写法。例如462. 最少移动次数使数组元素相等 II 题就不能采用 >>> 写法。

循环不变原则

跟踪循环中变化的细节是困难的，因此我们需要找到一些在整个循环过程中都不会发生变化的「量」或「关系」，以便得到循环结束后某些确定的结论。

if nums[c]<target: #1
    l=c+1 
else: #2
    r=c-1 

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于target。
• 对于#2行，若进入该分支，则 r 下标更新后其右侧元素「必」大于等于target。

在理解了「循环不变」原理后，编写这个版本的代码时尝试寻找 l 或 r 更新后是否能有类似target必在或必不在某个确定的范围的「循环不变」关系。

模板一(错位终止，左闭右闭)

标志——

• l,r=0,n-1
• while l<=r
• l=c+1,r=c-1
• l=r+1(终止时)

四种一般情形——

• 情形1: 大于等于。有相等元素时返回等于下标，否则返回刚好大于下标，否则返回 -1。（704题要求返回等于下标或-1）
• 情形2: 大于。不考虑相等，返回刚好大于下标，否则返回-1。
• 情形3: 小于等于。有相等元素时返回等于下标，否则返回刚好小于下标，否则返回 -1。（704题要求返回等于下标或-1）
• 情形4: 小于。不考虑相等，返回刚好小于下标，否则返回-1。

错位终止

while l<=r:

结束时必有： r = l - 1

证明示例如下：

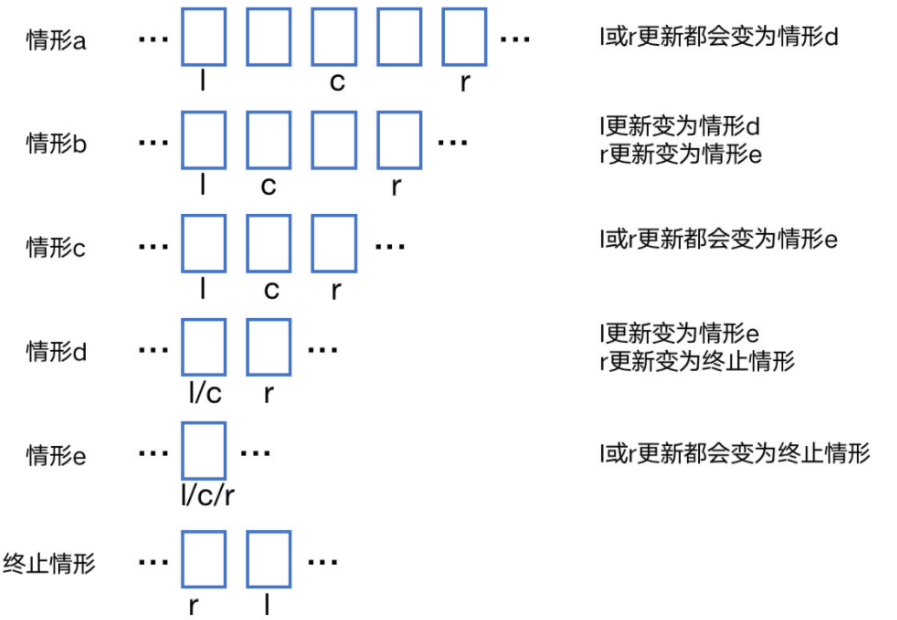
左闭右闭

l 与 r 的初始取值为：l,r=0,n-1
常规思路，[l,r] 刚好覆盖所有元素。
注意：如果模板二也采取左闭右闭的形式，可能会报错，后有详细解释。

情形1：大于等于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n-1
    while l<=r:
        c=l+(r-l)//2
        if nums[c]<target: #1
            l=c+1
        else: #2
            r=c-1
    #return l if (l!=n and nums[l]==target) else -1 # 处理相等返回情形
    return l if l!=n else -1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于 target。
• 对于#2行，若进入该分支，则 r 下标更新后其右侧元素「必」大于等于 target。
• 结束时，由于 l 左侧元素必小于 target，所以下标 l 对应元素必大于等于 target。
• (特殊)若 nums 所有元素均小于 target:由[循环不变]原则可知 r 保持不变(n-1)，l 不断右移直至 l=r+1=n。而真实情况应为 -1,所以有末尾的判断语句。

情形2：大于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n-1
    while l<=r:
        c=l+((r-l)>>1)
        if nums[c]<=target: #1
            l=c+1 
        else: #2
            r=c-1
    return l if l!=n else -1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于等于 target。
• 对于#2行，若进入该分支，则 r 下标更新后其右侧元素「必」大于 target。
• 结束时，由于 l 左侧元素必小于等于 target，所以下标 l 对应元素必大于 target。
• (特殊)若 nums 所有元素均小于等于 target:由[循环不变]原则可知 r 保持不变(n-1)，l 不断右移直至 l=r+1=n。而真实情况应为 -1,所以有末尾的判断语句。

情形3：小于等于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n-1
    while l<=r:
        c=l+(r-l)//2
        if nums[c]<=target: #1
            l=c+1
        else: #2
            r=c-1
    #return r if (nums[l]==target) else -1 # 处理相等返回情形
    return r

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于等于 target。
• 对于#2行，若进入该分支，则 r 下标更新后其右侧元素「必」大于 target。
• 结束时，由于 r 右侧元素必大于 target，所以下标 r 对应元素必小于等于 target。
• (特殊)若 nums 所有元素均大于 target:由[循环不变]原则可知 l 保持不变(0)，r 不断左移直至 r=l-1=-1。恰好与真实情况相同，所以无须像情形1或2那样添加判断语句。

情形4：小于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n-1
    while l<=r:
        c=l+(r-l)//2
        if nums[c]<target:
            l=c+1
        else:
            r=c-1
    return r

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于 target。
• 对于#2行，若进入该分支，则 r 下标更新后其右侧元素「必」大于等于 target。
• 结束时，由于 r 右侧元素必大于等于 target，所以下标 r 对应元素必小于 target。
• (特殊)若 nums 所有元素均大于等于 target:由[循环不变]原则可知 l 保持不变(0)，r 不断左移直至 r=l-1=-1。恰好与真实情况相同，所以无须像情形1或2那样添加判断语句。

模板二(相等终止，左闭右开)

标志——

• l,r=0,n
• while l<r
• l=c+1,r=c
• l=r(终止时)

相等终止

while l<r:

结束时必有： r = l

证明示例如下：

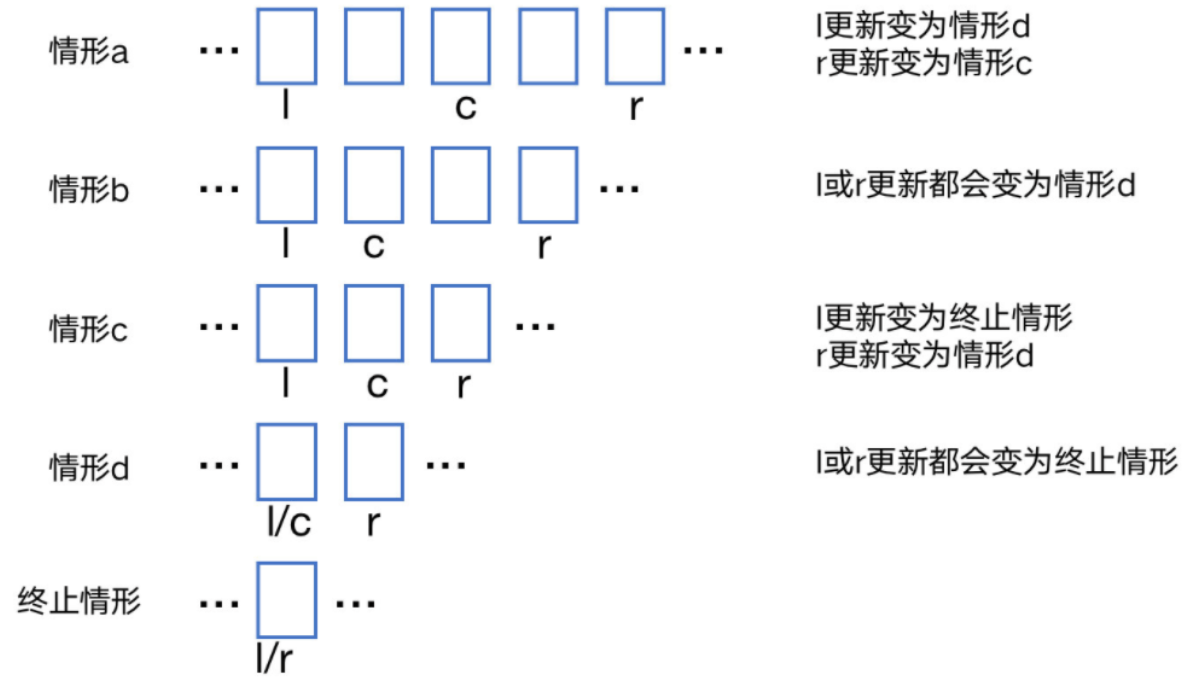
左闭右开

l 与 r 的初始取值为：l,r=0,n
错误示范，若采用左闭右闭 [l,r]:

• 由于 while 的条件是 l < r，当nums只有一个元素时，将无法进入while
• 当 target 大于 nums 中所有元素时，r = n 将是这一情况的一个标志，倘若 r 初始值为 n - 1，只看 r 的最终取值是无法判断为上述情况的，仍需要比较一次 target 与 nums 中的最后一个元素。
• 在后续「情形3」和「情形4」的代码中还可以进一步体会将 r 初始值设置为 r = n 带来的统一返回值的好处。

情形1：大于等于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n
    while l<r:
        c=l+(r-l)//2
        if nums[c]<target: #1
            l=c+1
        else: #2
            r=c
    #return r if (l!=n and nums[r]==target) else -1 # 处理相等返回情形
    return r if l!=n else -1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于 target。
• 对于#2行，若进入该分支，则 r 下标更新后r 及其右侧元素「必」大于等于 target。
• 结束时，由于 r 及其右侧元素必大于等于 target，所以下标 r 对应元素必大于等于 target。
• (特殊)若 nums 所有元素均小于 target:由[循环不变]原则可知 r 保持不变(n)，l 不断右移直至 l=r=n。而真实情况应为 -1,所以有末尾的判断语句。

情形2：大于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n
    while l<r:
        c=l+(r-l)//2
        if nums[c]<=target: #1
            l=c+1
        else: #2
            r=c
    return r if l!=n else -1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于等于 target。
• 对于#2行，若进入该分支，则 r 下标更新后r 及其右侧元素「必」大于 target。
• 结束时，由于 r 及其右侧元素必大于 target，所以下标 r 对应元素必大于 target。
• (特殊)若 nums 所有元素均小于等于 target:由[循环不变]原则可知 r 保持不变(n)，l 不断右移直至 l=r=n。而真实情况应为 -1,所以有末尾的判断语句。

情形3：小于等于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n
    while l<r:
        c=l+(r-l)//2
        if nums[c]<=target:
            l=c+1
        else:
            r=c
    #return r-1 if (nums[r]==target) else -1 # 处理相等返回情形
    return r-1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于等于 target。
• 对于#2行，若进入该分支，则 r 下标更新后r 及其右侧元素「必」大于 target。
• 结束时，由于 r 及其右侧元素必大于 target，所以下标 r-1 对应元素必小于等于 target。
• (特殊)若 nums 所有元素均大于 target:由[循环不变]原则可知 l 保持不变(0)，r 不断左移直至 r=l=0，即r-1=-1。恰好与真实情况相同，所以无须像情形1或2那样添加判断语句。

情形4：小于(target)

def binarySearch(nums,target):
    n=len(nums)
    l,r=0,n
    while l<r:
        c=l+(r-l)//2
        if nums[c]<target: #1
            l=c+1
        else: #2
            r=c
    return r-1

• 对于#1行，若进入该分支，则 l 下标更新后其左侧元素「必」小于 target。
• 对于#2行，若进入该分支，则 r 下标更新后r 及其右侧元素「必」大于等于 target。
• 结束时，由于 r 及其右侧元素必大于等于 target，所以下标 r-1 对应元素必小于 target。
• (特殊)若 nums 所有元素均大于 target:由[循环不变]原则可知 l 保持不变(0)，r 不断左移直至 r=l=0，即r-1=-1。恰好与真实情况相同，所以无须像情形1或2那样添加判断语句。

内置函数

使用前提：数组有序

python

Python中的二分函数为 bisect_left / bisect / bisect_right。
bisect_left返回「大于等于」x的(第一个)元素下标，若都小于x，返回最后一个元素下标+1（即类似n），使用的是「模版二」的情形1写法。

def bisect_left(a, x, lo=0, hi=None, *, key=None):
    """Return the index where to insert item x in list a, assuming a is sorted.
    The return value i is such that all e in a[:i] have e < x, and all e in
    a[i:] have e >= x.  So if x already appears in the list, a.insert(i, x) will
    insert just before the leftmost x already there.
    Optional args lo (default 0) and hi (default len(a)) bound the
    slice of a to be searched.
    """

    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    # Note, the comparison uses "<" to match the
    # __lt__() logic in list.sort() and in heapq.
    if key is None:
        while lo < hi:
            mid = (lo + hi) // 2
            if a[mid] < x:
                lo = mid + 1
            else:
                hi = mid
    else:
        while lo < hi:
            mid = (lo + hi) // 2
            if key(a[mid]) < x:
                lo = mid + 1
            else:
                hi = mid
    return lo

bisect与bisect_right用法相同，返回「大于」x 的(第一个)元素下标，若都小于x，返回最后一个元素下标+1（即类似n），使用的是「模版二」的情形2写法。

def bisect_right(a, x, lo=0, hi=None, *, key=None):
    """Return the index where to insert item x in list a, assuming a is sorted.
    The return value i is such that all e in a[:i] have e <= x, and all e in
    a[i:] have e > x.  So if x already appears in the list, a.insert(i, x) will
    insert just after the rightmost x already there.
    Optional args lo (default 0) and hi (default len(a)) bound the
    slice of a to be searched.
    """

    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    # Note, the comparison uses "<" to match the
    # __lt__() logic in list.sort() and in heapq.
    if key is None:
        while lo < hi:
            mid = (lo + hi) // 2
            if x < a[mid]:
                hi = mid
            else:
                lo = mid + 1
    else:
        while lo < hi:
            mid = (lo + hi) // 2
            if x < key(a[mid]):
                hi = mid
            else:
                lo = mid + 1
    return lo