Castle Defense

你需要最大化被数量最少的弓箭手保护的墙被弓箭手保护的数量。想到什么，对了，二分答案。

对 $check$ 函数进行思考。

令答案为 $m$。

如果一个点的值小于 $m$，则考虑将其变成 $m$，那么将这一段加在哪里呢？

设位置为：$x$，要加的值为 $y$。贪心一下很显然要将以 $x$ 为起点向右的一段长度为 $2r$ 的区间都加上 $y$。

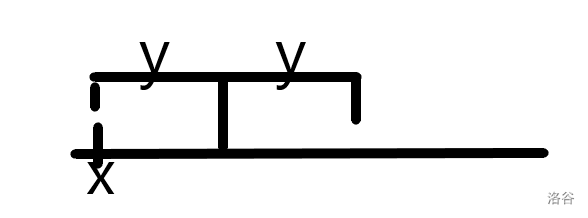
那么如何维护当前的值呢？看到单点查询，和区间加，相信很多人会想到线段树，但其实不用，差分数组即可维护。

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long 
int n,r,k;
const int N=(5e5+7)*2;
int a[N],b[N],c[N];
int max(int a,int b){
    return (a>b?a:b);
}
bool check(int k2){
    int sum=0;
    for(int i=1;i<=n;i++) c[i]=b[i];
    for(int i=1;i<=n;i++){
        c[i]+=c[i-1];
        if(c[i]<k2){
            //将以x为起点向右的一段长度为2r的区间都加上y.代码中i是x，x是y。
            int x=k2-c[i];
            sum+=x;
            c[i]+=x;
            c[i+2*r+1]-=x;
            if(sum>k) return 0;
        }
    }
    return 1;
}
signed main() {
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int l=0,r2=0,mid,ans;
    cin>>n>>r>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i+r+1]-=a[i];
        b[max(1,i-r)]+=a[i];
        r2+=a[i]+k;
    }
    while(l<=r2){
        mid=(l+r2)>>1;
        if(check(mid)) l=mid+1,ans=mid;
        else r2=mid-1;
    }
    cout<<ans;
    return 0;
}