初赛复习
$$\large\texttt{前言}$$
本文适合普及组到提高组的同学学习,并且尽量做到优秀的排版和通俗易懂,少用缩写。
本文设定为读者已经学习过C++语法、基础算法(如排序)、各种计算机基础名词、小学~初中数学
本文的写作顺序为由易至难,笔者按照自己的理解给知识点分了难度。
标有 $\checkmark$ 的为常考/出现过;标有“补”为拓展内容,只需了解;标有 $\bigstar$ 为每年几乎必考,加粗的内容为提炼过后的重点。
建议先预习CSP 2020 入门组第一轮/CSP 2020 提高组第一轮/CSP 2020 第一轮(初赛)模拟的前 $15$ 题。
迄今为止,初赛分为两个部分:
- 基础题:考察计算机科学和算法的基础,或许会有一些简单的数学。共 $15$ 题。
- 程序题:读程序写结果($3$ 题)+补全程序($2$ 题),难度依次递增。
这里只介绍基础题的部分,程序题由于知识点过散,需要大家自己多做题,多看代码,缕清思路。
如果有对文章的建议/问题勘误均欢迎私信或在下方留言!
本 blog 目前只发布在洛谷上,不接受任何形式的转载/抄袭,除非得到原作者 @159号程序员 的许可。
$$\Large\mathtt{\text{CSP初赛知识点梳理}}$$$$\mathtt{CSP\,\,\,PRE-KNOWLEDGE}$$
$$\tiny\text{本文内容较多,如果是想查找某一个特定的词语,可以在浏览器中使用 Ctrl + F 进行页面内搜索。}$$
$$\large\texttt{计算机}$$
-
计算机的分类 $\checkmark$
-
按年代分类
$ \begin{matrix} \text{年代\qquad} & \text{实现方式}\\\\ \text{1946\,至1958\qquad} & \text{电子管}\\\\ \text{1959\,至1964\qquad} & \text{晶体管}\\\\ \text{1965\,至1970\qquad} & \text{集成电路}\\\\ \text{1971\,至N/A\qquad} & \text{超大规模集成电路}\\\\ \end{matrix} $
-
按性能分类
巨型机>大/中型机>小型机>微型机=工作站。
补:一般按照规模大小、性能、能耗等分类。
- 巨型机(超级计算机,简称「超算」):速度极快,容量极高,体积极大。高速度,大容量,因而能够承担重大的科学研究,用于计算地震/太空/天气预报等复杂用途,我国的有:银河/天河等。
补:巨型机运算速度平均每秒千万次以上,存储容量千万位以上。
- 大/中型机:速度快,容量极高,体积大。高可靠性,可用性,服务型,主要用于顶尖科研领域。
补:大型机和超级计算机(旧称巨型机)的主要区别:
-
大型机使用专用指令系统和操作系统,巨型机使用通用处理器及 UNIX 或类 UNIX 操作系统(如 Linux)。
-
大型机长于非数值计算(数据处理),巨型长于数值计算(科学计算)。
-
大型机主要用于商业领域,如银行和电信,而巨型用于尖端科学领域,特别是国防领域。
-
大型机大量使用冗余等技术确保其安全性及稳定性,所以内部结构通常有两套。而巨型机使用大量处理器,通常由多个机柜组成。
-
为了确保兼容性,大型机的部分技术较为保守。
- 小型机:速度快,容量高,体积中。主要用于单位服务器/其他领域。
补:小型机采用精简指令集处理器,性能和价格介于PC服务器和大型主机之间的一种高性能 $64$ 位计算机。
补:小型机主要用于金融证券和交通等对业务的单点运行具有高可靠性的行业应用。
-
微型机:速度快,容量中,体积小。主要用于个人工作/处理数据,$20$ 世纪 $70$ 年代后非常普及(电脑大部分都是微型机)。各位同学面前的电脑、笔记本、手机等等基本上都是微型机。
-
工作站:速度快,容量中,体积小。用于辅助微型机工作。
-
-
空间换算 $\bigstar$
$ \begin{matrix} \text{「小」单位\qquad} & \text{「大」单位}\\\\ \text{8 bit(比特)\qquad} & \text{1 B(Byte/字节)}\\\\ \text{1024 B\qquad} & \text{1 KiB(Kilobyte)}\\\\ \text{1024 K(iB)\qquad} & \text{1 MiB(Millonbyte)}\\\\ \text{1024 M(iB)\qquad} & \text{1 GiB(Gigabyte)}\\\\ \text{1024 G(iB)\qquad} & \text{1 TiB(Terabyte)}\\\\ \end{matrix} $
$\text{iB}$ 结尾的是 $1024$ 单位一换算,$\text{B}$ 结尾的是 $1000$ 单位一换算(如 $\text{KB}$,上表中没有),这就是我们买的 $\text{512GiB}$ 硬盘有时候显示不到 $\text{500GiB}$ 的原因。(单位不同)
考试时注意审题。
-
重要贡献人员 $\bigstar$
-
阿兰·艾伦·图灵(英):数学家,逻辑学家,计算机科学/人工智能之父,首次提出了计算机科学理论。计算机界的最高奖项“图灵奖”以他命名,被称为“计算机界的诺贝尔奖”。
-
冯·诺依曼(美):科学家,现代计算机之父,首次提出了存储程序控制原理,称为“冯·诺依曼结构”。
-
克劳德·香农(美):科学家,创造了信息论,提出了某种信息从一处传送到另一处所需的全部设备所构成的系统。
-
习题
-
-
计算机的构成 $\checkmark$
要想实现计算机的基础功能,计算机必须由运算器、存储器、控制器、输入设备、输出设备构成,缺少前两者就无法正常启动计算机,即为“冯·诺依曼结构”。
- CPU(Central Processing Unit):中央处理器,由运算器(计算)+控制器(指挥)+寄存器组成。
计算机的核心部件,被称为计算机的“大脑”,又称“微处理器”。
-
内存储器:简称“内存”,用于电脑内部的存储。相对外存而言,读写速度快,但是存储空间小,并且存储在 RAM 里的数据断电后会丢失。注意与“外存(硬盘等)”区分开。
-
RAM(Random Access Memory):随机存取存储器,与CPU直接交互数据,可随时读写,断电数据全部丢失。
-
ROM(Read-Only Memory):只读存储器,只能读出无法写入信息。信息一旦写入后就固定下来,断电数据不会丢失,故又称为固定存储器。
-
外存储器:简称“外存”,用于处置长期保存的数据,一般处于电脑外部,断电后数据不会丢失。相对内存而言,外存读写速度慢,但存储容量大。主要包括硬盘、光盘、U 盘(USB闪存盘)等类型。
-
输入设备:在计算机与人交互时,接受外部命令或者需要加工的数据。常用的输入数据包括键盘、鼠标、麦克风、摄像头等。
-
输出设备:在计算机与人交互时,将处理结果以人类能够识别/感受的方式呈现出来的设备。常有的输出设备包括显示器、音响、打印机等。
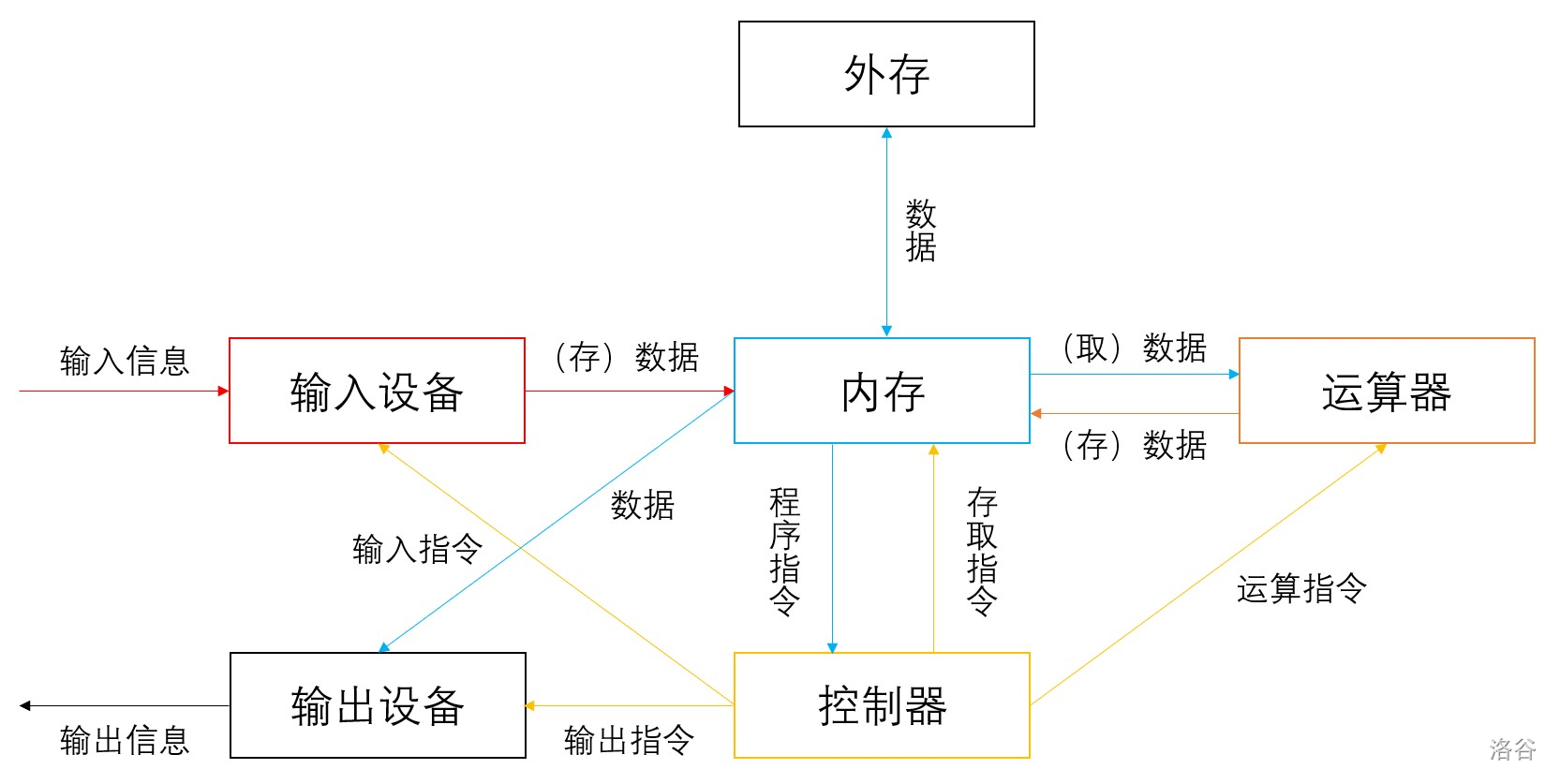
如上图,为各个设备之间的关系,不同设备用不同颜色进行表示。
-
关于CPU $\checkmark$
-
访问速度:寄存器>高速缓存>内存>外存。
-
历史:出现于 $20$ 世纪 $70$ 年代。
-
断电后数据保留于 ROM 和外存。
-
-
文件扩展名(注意不是“拓展名”) $\checkmark$
-
图像存储:jp(e)g/png/pic/bmp/gif。
-
音频存储:mp3/wav。
-
视频存储:mp4/avi/mpeg/flv/rmvb/rpm。
-
-
计算机语言常识 $\bigstar$
-
机器语言/机器码:最早的语言,计算机能识别的语言,由二进制数字 $0/1$ 组成,速度快,人类编码难度高,一般由计算机自动转换。
-
汇编语言:用符号代替二进制数,计算机不能直接识别,需要用编译器进行编译,难度依然很大,目前除了对性能要求极高的需求以外不被使用。
-
高级语言:如今的编程语言(C++,JAVA 等),需要用编译器,难度小,分为编译方式和解释方式两种编译方式。
-
编译方式(C++):先对整个程序进行编译(会进行多次分析),再执行程序。速度快(进行多次编译对程序进行优化)。
-
解释方式(Python/PHP):扫描一行解释一行,速度慢(无法进行优化)。
-
-
习题:
-
-
ASCII 码 $\checkmark$
ASCII 码(American Standard Code for Information Interchange)是美国国家交换标准代码,现成为世界交换代码标准。
ASCII 码是一种用 $8$ 个比特组成的二进制编码(即一个字节),用于表示 $128$ 个国际通用字符。
$ \begin{matrix} \text{位置\qquad} & \text{分类} &\text{可见性}\\\\ 0\sim 31,\,127\qquad & \text{控制字符或通信专用字符} & \text{N}\\\\ 32\qquad & \text{空格} & \text{Y/N}\\\\ 33\sim 47,\,58\sim 64,\,94\sim 96, 126\qquad & \text{特殊字符(除字母/数字/空格/控制字符外的其他字符)} & \text{Y}\\\\ \checkmark\,48\sim 57\qquad & \text{数字(按大小升序)} & \text{Y}\\\\ \checkmark\,65\sim 90\qquad & \text{大写字母(按字母表升序)} & \text{Y}\\\\ \checkmark\,97\sim 122\qquad & \text{小写字母(按字母表升序)} & \text{Y}\\\\ \end{matrix} $
补:$2^8 = 256$,$2^7 = 128$,这是因为在 ASCII 码中,把二进制最高位为 $0$ 的数字都称为基本的 ASCII 码,其范围是 $0\sim 127$;把二进制最高位为 $1$ 的数字都称为拓展的 ASCII 码,其范围是 $0\sim 256$。
补:一个汉字在计算机中占 $2$ 个 $\text{Byte}$。
-
机器数与真值 $\bigstar$
计算机中要处理的整数有“无符号”和“有符号”之分,“无符号”整数顾名思义就是不考虑正负的整数,可以直接用二进制表示,故只讨论“有符号”整数。
-
原码:原码将一个整数表示成符号位+二进制串。符号位上,$0$ 表示正数,$1$ 表示负数。
但是,用这种方法表示的数进行两个异号数相加或两个同号数相减时很不方便,而且 $0$ 的表示不唯一,于是引入了“反码”和“补码”。
补:原码中,$0$ 的表示有两种: $+0$ 或 $-0$,两种的区别在于符号位,$+0$ 表示为 $00000000$,$-0$ 表示为 $10000000$。
-
反码:对于一个正数,反码就是其原码;对于一个负数,反码就是除符号位外,原码的各位全部取反,即 $0$ 变 $1$,$1$ 变 $0$。
如:$x_{\text{原}}=01000101, x_{\text{反}}=01000101$。
$\,\,\,\,\,\,\,\,\,\,x_{\text{原}}=11000101, x_{\text{反}}=10111010$。
补:多数计算机不采用反码表示数值。
-
补码:对于一个正数,补码就是其原码;对于一个负数,补码等于反码+1。
如:$x_{\text{原}}=01000101, x_{\text{补}}=01000101$。
$\,\,\,\,\,\,\,\,\,\,x_{\text{原}}=11000101, x_{\text{补}}=10111011$。
-
-
逻辑运算 $\checkmark$
-
逻辑非:$!$ 或 $\neg$,操作数的反值($!1=0,!0=1$)。
-
逻辑与:$\&\&$ 或 $\land$,全部操作数都为真,结果才为真($1\land1=1,1\land 0=0,0\land 1=0,0 \land 0=0$)。
-
逻辑或:$\|$ 或 $\lor$,至少一个操作数为真,结果才为真。($1\lor 1=1,1\lor 0=1,0\lor 1=1,0\lor 0=0$)
-
运算优先级:逻辑非>逻辑与>逻辑或。
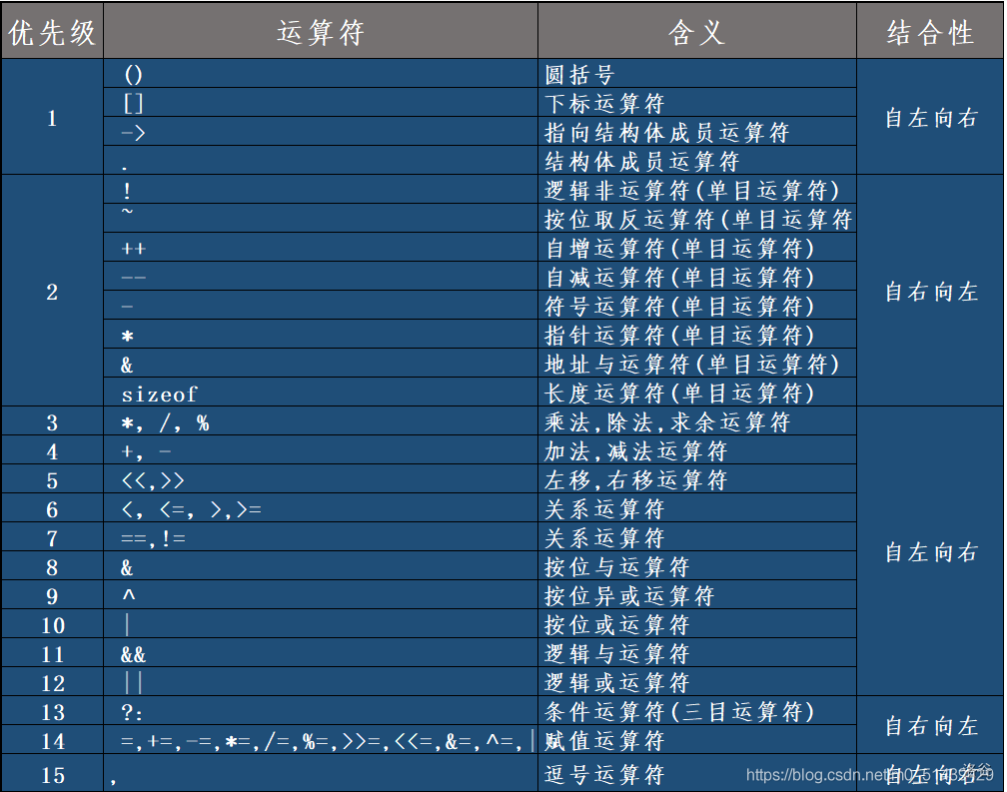
可以简单理解为:非(乘方)>与(乘/除法)>或(加/减法)。
-
按位与:$\&$,参加运算的两个数,按二进制位进行“与”运算。如果两个相应位同时为 $1$,该位结果为 $1$,否则为 $0$。(负数以补码形式参加运算)
-
按位或:$|$,参加运算的两个数,按二进制位进行“或”运算。如果两个相应位有至少一个 $1$,该位结果为 $1$,否则为 $0$。(负数以补码形式参加运算)
-
按位异或:$^{\wedge}$(注意与“逻辑与”区分)或 $\operatorname{xor}$,参加运算的两个数,按二进制位进行“异或”运算。如果两个相应位为“异”(值不同),则该位结果为 $1$,否则为 $0$。(负数以补码形式参加运算)
特别的,在进行按位运算时,如果位数不够,需要在位数少的数前补 $0$。例如:$13 | 2=1101|0010=1111$。
-
-
逻辑表达式:由逻辑运算组合而成,返回值只有 T(True) 和F(False),C++ 中 $0$ 表示假、非 $0$ 表示真。
如果逻辑表达式由多个组合,需要从右往左依次判断,最后得出答案。这种性质被称为右结合性。
例如:
<表达式1>?<表达式2>:<表达式3>?<表达式4>:<表达式5>。执行的时候是从表达式 $3$ 开始判断是否为真,然后从右往左执行每一个表达式,依次向上回溯,最后得出答案。
$$\large\texttt{数据结构}$$
-
图论
-
基本概念/术语 $\checkmark$
-
顶点/节点(Vertex/Node),简称点。
-
边(Edge):节点之间的连线。
-
完全图:任意两点都有边相连,一个 $n$ 个节点完全图的边数 $ C_n^2= \dfrac{n(n-1)}{2}$ 。(对于组合数 $C^2_n$ 的具体说明详见“数学”部分)
-
简单路径:两点之间通过不重复的边相连。
-
连通图:任意两点都可以直接/间接到达,注意区别于完全图,完全图属于连通图,连通图不一定属于完全图。
-
有向图:边是有方向的($e = u\rightarrow v$)。
-
无向图:边是无方向的($e = u\leftrightarrow v$)。
-
环:对于一个回路 $w$,若 $v_0=v_k$ 是该回路点序列中唯一重复出现的点对,则 $w$ 是一个环。
特别的,如果环 $w$ 只有一个点,则被称为“自环,即 $e=(u,v), u=v$。
-
入度:以顶点 $v$ 为终点的边的条数为该节点的入度。
-
出度:以顶点 $v$ 为起点的边的条数为该节点的出度。
-
-
树 $\bigstar$
-
基本概念/术语
-
树:一个长得像真实生活中倒置(即根在上、叶子在下)的树的图,任意两点之间的简单路径有且只有一条。树是一棵连通且无环的图,边数 $=n−1$。
-
根节点:树最上层的节点,一棵树有且只有一个。
-
深度:到根结点的路径上的边数。
-
高度:所有结点的深度的最大值。
-
叶节点:没有子结点的结点。
-
父亲:对于除根以外的每个结点,从该结点到根路径上的第二个结点。根结点没有父结点。
-
祖先:一个结点到根结点的路径上,除了它本身外的结点。根结点的祖先集合为空。
-
子节点:如果 $u$ 是 $v$ 的父亲,那么 $v$ 是 $u$ 的子结点。子结点的顺序一般不加以区分,二叉树是一个例外,有左儿子/右儿子之分。
-
兄弟:同一个父亲的多个子结点互为兄弟。
-
后代:如果 $u$ 是 $v$ 的祖先,那么 $v$ 是 $u$ 的后代。
-
子树:删掉与父亲相连的边后,该结点所在的子图。
-
-
二叉树 $\bigstar$
-
前/先序遍历:根 $\rightarrow$ 左子树/儿子 $\rightarrow$ 右子树/儿子。
-
中序遍历:左子树/儿子 $\rightarrow$ 根 $\rightarrow$ 右子树/儿子。
-
后序遍历:左子树/儿子 $\rightarrow$ 右子树/儿子 $\rightarrow$ 根。
-
遍历的特殊结论
-
前/先序遍历 + 中序遍历 = 确定二叉树。
-
后序遍历 + 中序遍历 = 确定二叉树。
-
-
特殊的二叉树及其性质
-
满二叉树/完美二叉树:所有叶结点的深度均相同的二叉树称为满二叉树/完美二叉树。
满二叉树的第 $k$ 层有 $2^{k-1}$ 个节点,任意 $k$ 层二叉树最多有 $2^{k-1}$ 个节点。
若在任意一棵满二叉树中,有 $n_0$ 个叶子节点,有 $n_2$ 个度为 $2$ 的节点,则有 $n_0=n_2+1$。
$n$ 个节点的满二叉树深为 $\log n+1$
-
完全二叉树:只有最下面两层结点的度数可以小于 $2$,且最下面一层的结点都集中在该层的最左侧。
-
对于一棵满二叉树/完美二叉树,其深度为 $k$,则其节点总数为 $2^k-1$,此结论可逆。
-
对于一棵满二叉树/完美二叉树/完全二叉树,若任意节点(除叶节点外)的编号为 $i$,其左儿子的编号为 $2i$,右儿子的编号为 $2i + 1$。此结论可逆,证明显然。
二叉树的第 $k$ 层至多有 $2^{i-1}(i\ge1)$ 个节点。
-
-
习题
-
-
栈 $\checkmark$
-
定义/术语
-
定义:有一叠碗,每一次取的时候取最上面的出来,放的时候放到最上面,先进来的后出去,后进来的先出去,这就是后进先出(last in first out)表,简称 LIFO 表。
-
栈顶:栈最顶端的元素。
-
栈底:栈最底端的元素。
-
-
操作
-
push(x)往栈顶前添加一个元素 $x$。 -
pop()从栈顶弹出(删除)一个元素。 -
top()返回栈顶的值。 -
empty()返回是否为空。($1$ 为空,$0$ 为非空) -
size()返回栈里的元素个数。
-
-
-
队列 $\checkmark$
-
定义/术语
-
定义: 与生活中的队列相同,一条队伍,没有人会插队,大家都按队伍的规矩排好。先进来的先出去,后进来的后出去,这就是先进先出(first in first out)表,简称 FIFO 表。
-
队首/队头:队列的第一项。
-
队尾:队列的最后一项。
-
操作
-
push(x)往队尾后添加一个元素 $x$。 -
pop()从队首弹出(删除)一个元素。 -
front()返回队首的值。 -
empty()返回是否为空。($1$ 为空,$0$ 为非空) -
size()返回队列里的元素个数。
-
-
-
链表 $\checkmark$
-
定义/特点
-
定义:链表和数组都可用于存储数据,其中链表通过指针来连接元素,而数组则是把所有元素按次序依次存储。
-
链表可以方便地删除、插入数据,操作次数是 $O(1)$,但是访问任意数据时操作次数是 $O(n)$。
-
链表不可以随机访问任意数据!
-
-
习题
-
-
字符串 $\checkmark$
-
定义:字符串指一串字符组成的串。
-
子串:子串被定义为字符串中任意个连续的字符组成的子序列,子串个数 $=\dfrac{n(n+1)}{2}+1$,非空子串的个数 $=\dfrac{n(n+1)}{2}$(无非就是少了空子串的 $+1$)
-
前/中/后缀表达式:
-
前缀表达式:一种没有括号的表达式,与中缀表达式不同的是,将运算符写在前面,操作数写在后面。如:前缀表达式 $-1+2\,\,\,3$ 的中缀形式为 $1-(2+3)$。
-
中缀表达式:与平常使用的表达式相同,有括号且运算符在操作数中间。
-
后缀表达式:与前缀表达式相反,将操作数写在前面,运算符写在后面。如:后缀表达式 $1\,\,\,2\,\,\,3+-$ 的中缀形式为 $1-(2+3)$。
-
前/中/后缀表达式的转化
-
前/后缀表达式转中缀表达式
-
画出表达式树:表达式树是一种特殊的树,叶节点是操作数,其他节点为运算符
-
将表达式树前序遍历,可得前缀表达式;中序遍历可得中缀表达式;后序遍历可得后缀表达式。
-
-
中缀表达式转前/后缀表达式
-
给中缀表达式加上括号:$$1-2+3\rightarrow ((1-2)+3)$$
-
把运算符移到括号前/后面(移到前面为前缀表达式,反之亦然):$$(1-(2+3))\rightarrow ((12)-3)+$$
-
删去括号,剩下的即为最终解:
$$(1(23)+)-\rightarrow 12-3+$$
也可以用上文的“表达式树”做,比较复杂,推荐以上加括号的方法。
-
-
-
-
$$\large\texttt{数学}$$
-
最大公约数/最小公倍数 $\checkmark$
-
最大公约数:两/多个数之间最大的共有因数。
-
最小公倍数:两/多个数之间最小的共有倍数。
-
具体求法
- 短除法:先用这几个数的公约数连续去除,一直除到所有的商互质为止,然后把所有的能被所有数字整除的除数连乘起来,所得的积就是这几个数的最大公约数。最小公倍数为左侧和下侧所有数的乘积。具体写法如下图:
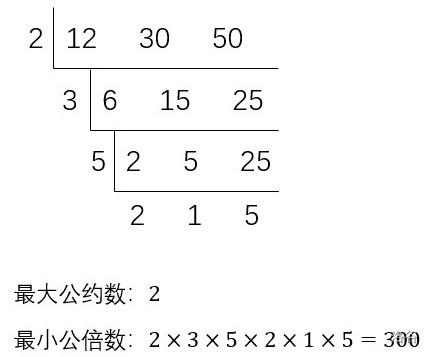
可以得到规律:最大公约数为左侧能被所有数字整除的数的乘积(此处只有 $2$。$3$ 不是是因为 $50$ 不能整除 $3$);最小公倍数为左侧和下侧所有数的乘积。
补:实际上,上图中除到 $6\quad15\quad25$ 互质就可以了,这样写只是方便初学者理解。
显然,短除法并不适合较大的数字,运算会特别麻烦,出错率高。所以辗转相除法就应运而生了。
-
辗转相除法(欧几里得算法):辗转相除法是用来求两个正整数最大公约数的算法。以除数和余数反复做除法运算,当余数为 $0$ 时,取当前算式除数为最大公约数。
例如:求 $437$ 和 $323$ 的最大公约数。
$437\div 323=1\cdots\cdots114$
$323\div 114=2\cdots\cdots95$
$114\div 95=1\cdots\cdots19$
$95\div 19=5(\cdots\cdots0)$
$\therefore \gcd(437,323)=19$
-
-
习题
-
-
进制 $\bigstar$
-
十进制转 $n$ 进制(以二进制为例)
把十进制数每次除以 $n$ 求余数,然后把余数逆序写出来。
简单记忆:整数部分,辗转除 $n$,取余。小数部分,辗转乘 $n$,取整数部分。
例如 $13_{(10)}$,先 $\div 2$,商 $6$ 余 $1$。
$6 \div 2 = 3 \cdots\cdots 0$
$3 \div 2 = 1 \cdots\cdots 1$
$1 \div 2 = 0 \cdots\cdots 1$
$13_{(10)}=1101_{(2)}$
如何证明此方法的正确性?
一个二进制串可以用位值表示出来:
$x_{(2)} = a_{n-1}\times2^{n-1}+a_{n-2}\times2^{n-2}+\cdots+a_{1}\times2^{1}+a_{0}\times2^{0}$
其中,$a_{n-1}\times2^{n-1}\sim a_{1}\times2^{1}$ 都是 $2$ 的倍数,除了最后一项 $a_{0}\times2^{0}$ 不是。(原因是幂次为 $0$)
$x_{(2)}\div 2=q\cdots \cdots r$
因为 $a_{0}$ 不是 $2$ 的倍数,所以 $r=a_{0}\times2^{0}=a_{0}\times1=a_{0}$。
这样就得到了 $x_{(2)}$ 的最后一位。
显然有:
$q=\dfrac{1}{2}x$
$\;\;\;=\dfrac{a_{n-1}\times2^{n-1}\cdots+a_{1}\times2^{1}}{2}$
$\;\;\;=a_{n-1}\times2^{\color{red}{n-2}}\cdots+a_{1}\times2^{\color{red}0}$
观察上式,此时的 $q$ 的末尾位正好是 $x$ 的次末尾位,令 $x'=q$,$x'\div 2=q'\cdots r'$。
此时 $r=a_{1}\times2^{0}$,按照上面的过程不断辗转递推即可得出答案。
-
$n$ 进制转十进制(以二进制为例)
按位转换,第 $i$ 位的数字乘以要转换的进制的 $n−1$ 次幂即可。
$\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,0\qquad\,\,\,\,\,\,\,\,0\qquad\,\,\,\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,0\qquad\,\,\,\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,0$
$1\times2^7+0\times2^6+0\times2^5+1\times2^4+0\times2^3+1\times2^2+1\times2^1+0\times2^0=150_{(10)}$
$\,\,\,\,\,0.\qquad\,\,\,\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,0\qquad\,\,\,\,\,\,\,\,1\qquad\,\,\,\,\,\,\,\,$
$1\times2^{-1}+0\times2^{-2}+1\times2^{-3}=0.625_{(10)}$
-
$n$ 进制转 $m$ 进制
以十进制作为中转,先将 $n$ 进制转为十进制,再将十进制转为 $m$ 进制。
-
常用进制的英文
-
$16$ 进制:H(Hexadecimal)
-
$10$ 进制:D(Decimal)
-
$8$ 进制:O(Octonary)
-
$2$ 进制:B(Binary)
-
-
习题
-
-
排列组合 $\bigstar$
-
加法原理:完成一项工作有 $n$ 种方法,$a_i(1\le i \le n)$ 代表完成第 $i$ 类方法的数目,共有 $S=a_1+a_2+\cdots+a_{n-1}+a_n$ 种不同的方法。
-
乘法原理:完成一项工作有 $n$ 个步骤,$a_i(1\le i \le n)$ 代表完成第 $i$ 个步骤的数目,共有 $S=a_1\times a_2\times \cdots\times a_{n-1}\times a_n$ 种不同的方法。
-
排列(Arrangement/Permutation)
-
定义:从 $n$ 个不同元素中,任取 $m$($m\le n$)个元素按照一定的顺序排成一列,读做从 $n$ 个不同元素中取出 $m$ 个元素的一个排列,记为 $A_n^m$(或 $P_n^m$)。
-
计算公式:$A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\dfrac{n!}{(n-m)!}$
其中, $!$ 表示阶乘,例如 $6!=1\times 2 \times 3\times 4\times 5\times 6$,特别规定 $0!=1$。
-
证明:第 $1$ 个位置可以选 $n$ 个元素,第 $2$ 个位置由于先前已经选了一个,还可以选 $(n-1)$ 个元素,以此类推,第 $m$ 个可以选 $(n-m+1)$ 个元素。又根据上述的乘法原理,将所有的选法串联起来,因此得到上式。
-
全排列:排列的一种特殊情况,此时 $m=n,n-m=0$,刚刚规定过 $0!=1$,所以 $A_n^n=n!=1\times 2\times 3\cdots \times n$。
-
-
组合(Combination)
-
定义:从 $n$ 个不同元素中,任取 $m$($m\le n$) 个元素组成一个集合,读做从 $n$ 个不同元素中取出 $m$ 个元素的组合。即不关心被选元素的顺序。记为 $C_n^m$。
-
公式:$C_n^m=\dfrac{A_n^m}{m!}=\dfrac{n!}{m!(n-m)!}$
-
证明:如果 $n$ 个元素中选 $m$ 个且关心顺序,为 $A_n^m$。但是此时不关心顺序了,就需要去掉重复的,同样选出来的 $m$ 个元素,还要进行全排列,即除掉 $m!$,因此展开后得到上式。
组合数也常用 $\dbinom{n}{m}$ 表示,读作“$n$ 选 $m$”,更为清晰明了。
-
-
排列组合九大解题技巧(按个人认为的理解难度排序)
-
先选后排:先将元素选出来,再进行排列,非常有效的降低问题的复杂度。
-
特殊优先:特殊元素,优先处理;特殊位置,优先考虑。
-
分排用直排:$n$ 个元素,从中选出 $m$ 个,将这 $m$ 个元素排成若干排。分排问题的排列可以看做一排,避免考虑了复杂的前后排列,简化了问题。
$S=A_n^m$
-
分类法:当计算符合条件的数目比计算不符合条件数目简单时,将问题分成若干类,逐个求解,与“排除法”相对。
-
排除法:当计算符合条件的数目比计算不符合条件数目复杂时,简称正难则反。排除不符合要求的,剩下的就是符合题目要求的。与“分类法”相对。
-
捆绑法:$n$ 个不同元素排成一列,要求 $m$ 个元素必须相邻。可以特殊优先,把 $m$ 个元素捆绑在一块单独处理。
$S=A_{n-m+1}^{n-m+1}\times A_m^m$
-
插空法:$n$ 个不同元素排成一列,要求 $m$ 个元素不能相邻。先把不用特殊处理的元素进行排列,再把甲乙进行插空。
$S=A_{n-m}^{n-m}\times A_{n-1}^{m}$
-
隔板法/插板法:将 $n$ 个相同元素分成 $m$ 组,每组至少有一个元素。相当于把 $m-1$ 个隔板插到 $n$ 个元素形成的 $n-1$ 个空隙里。
$S=C_{n-1}^{m-1}$
-
定序: $n$ 个元素的全排列中有 $m$ 个元素必须定序排列,这 $m$ 个元素相邻或不相邻不受限制。
$S=\dfrac{A_n^n}{A_m^m}$
-
-
第一抽屉原理:【施工中】
-
习题
-
-
质数 $\checkmark$
-
定义:在大于 $1$ 的自然数中,除了 $1$ 和它本身以外不再有其他因数的自然数。否则称为合数。
特别的,$1$ 既不是质数也不是合数。
-
$100$ 以内的质数(共 $25$ 个):$2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97$,$91$ 是合数,但容易误以为是质数。
-
习题
-
$$\large\texttt{复杂度}$$
一个问题有很多种不同的算法,如何评价一个算法的好坏呢?这就需要时间复杂度和空间复杂度来衡量了。
-
定义
渐进时间复杂度,用符号 $\mathcal{O}$ 表示。一个算法里语句的执行次数可以用一个式子表示,取这个式子的最高次项且忽略系数表示该算法的时间复杂度。例如,一个程序的语句执行次数为 $2n+3n^2+9+8n$,则该算法的时间复杂度为 $\mathcal{O}(n^2)$。
-
常量
常量,即永远不变的量,例如,$1$ 就是 $1$,它永远不可能等于 $2$。在时间复杂度里,只要不随着输入数据规模的大小增长而增长的量,就被称之为常量,在计算中省去不写。
特别的,如果代码中出现了宏定义,那么宏定义的值依旧是常量,因为它不随着输入数据规模的大小而改变。
-
示例
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j];本代码中,
cin >> a[i][j]执行了 $n^2$ 次,所以时间复杂度为 $\mathcal{O}(n^2)$。for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j]; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> b[i][j];本代码中,
cin >> a[i][j]执行了 $n^2$ 次,cin >> b[i][j]也执行了 $n^2$ 次,忽略系数,时间复杂度还是 $\mathcal{O}(n^2)$。for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j]; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) for(int k = 1; k <= n; k++) cin >> b[i][j];本代码中,
cin >> a[i][j]执行了 $n^2$ 次,cin >> b[i][j]执行了 $n^3$ 次,取最高次项,时间复杂度是 $\mathcal{O}(n^3)$。 -
符号
$T(n)$ 表示时间复杂度,$T(n)=$ 后跟一个符号:
$\Theta$,
theta,等于。$\mathcal{O}$(也可写作 $O$),
big-oh,小于等于。$\Omega$,
big-omega大于等于。$o$,
small-oh小于。$\omega$,
small omega大于。 -
非递归程序的时间复杂度的计算
非递归程序的时间复杂度计算一般都比较简单,直接数循环。大多数算法都适用于此,但是也有例外,例如二分等,需要特别留心。
-
递归程序&主定理
假设某算法的计算时间表示为递归式:
$$T(n)=2T(\dfrac{n}{2})+n\operatorname{log}n$$$$T(1)=1$$
求该算法的时间复杂度。
- 直接代入递归求解
$$1.T(n)=2T(\frac n2)+n\log n$$
$$=4T(\frac n4)+2\times\frac n2\log \frac n2+n\log n$$
$$=8T({n\over8})+n\log{n\over4}+n\log{n\over2}+n\log n$$
$$=\dots$$
$$T(n)=\sum_{i=0}^{\log n}n\log\frac n{2^i}$$
$$=n\sum_{i=0}^{\log n}\log\frac n{2^i}$$
$$=n\sum_{i=0}^{\log n}\log2^i$$
$$=n\sum_{i=0}^{\log n}i$$
$$=\Theta(n\log^2n)$$
$$2.T(n)=T(n/2)+n\log n$$
$$=T(n/4)+\frac{n}{2}\log \frac{n}{2}+n\log n$$
$$=n\log n+\frac{n}{2}\log \frac{n}{2}+\frac{n}{4}\log \frac{n}{4}+\frac{n}{8}\log \frac{n}{8}+\ldots$$
$$\text{上式}\ge n\log n$$
$$\text{上式}\le n\log n+\frac{n}{2}\log {n}+\frac{n}{4}\log {n}+\frac{n}{8}\log {n}+\ldots=2n\log n$$
$$\therefore\quad=\Theta(2n\log n)=\mathcal{O}(n\log n)$$
虽然此方法计算量较大,但是是初学者不二的选择。如果追求卷面,可以学习主定理。
-
主定理:将一个规模为 $n$ 的问题,分治成 $a$ 个 $\lceil\dfrac{n}{b}\rceil$ 的子问题,每次带来的额外计算为 $\mathcal{O}(n^d)$,可得到以下关系式:
$$T(n)=aT(\lceil\dfrac{n}{b}\rceil)+\mathcal{O}(n^d)$$$$(\text{for \,constants\,}a>0,b>1,d\ge0),\text{then}:$$
$$T(n) = \begin{cases} \mathcal{O(n^d)} & if\quad d>\operatorname{log}_ba\\ \mathcal{O(n^d\operatorname{log}n)} & if\quad d=\operatorname{log}_ba\\ \mathcal{O(n^{\operatorname{log}_ba})} & if\quad d<\operatorname{log}_ba\\ \end{cases} $$
个人理解:$$T(n)=aT(\dfrac{n}{b})+\mathcal{f}(n)$$
若 $n^{\log _{b} ^{a}} >f(n)$ 则 $T(n)=n^{\log _{b} ^{a}}$
若相等 则 $T(n)=f(n) \times \log(n) $
若小于且 $a f(\frac{n}{b}) \le cf(n) \ c$ 为满足条件的最大值,若 $c<1$ 则 $T(n)=f(n)$,否则不适用于主定理。
-
空间复杂度 $\checkmark$
-
定义:空间复杂度较时间复杂度来说简单许多,可以直接数。符号同时间复杂度。
-
计算
$$ \begin{matrix} &\text{变量 int\,a}&\text{一维数组 int\,a[n]}&\text{二维数组 int\,a[n][n]}&\cdots\\ \text{空间复杂度}&\mathcal{O}(1)&\mathcal{O}(n)&\mathcal{O}(n^2)&\cdots\\ \end{matrix} $$
可见,只需要数数组有几维即可,其他注意事项(如常数等)与时间复杂度相同。
-
$$\large\texttt{排序算法}$$
初赛里常考的的排序大多分为 $8$ 种:选择排序、冒泡排序、插入排序、快速排序、希尔排序、堆排序、归并排序、基数排序。
$$ \begin{matrix} &\text{选择排序}&\text{冒泡排序}&\text{插入排序}&\text{快速排序}&\text{希尔排序}&\text{堆排序}&\text{归并排序}&\text{基数排序}&\\ \text{一般情况}&\mathcal{O}(n^2)&\mathcal{O}(n^2)&\mathcal{O}(n^2)&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(n^{1.3})&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(d(n+r))\\ \text{最坏情况}&\mathcal{O}(n^2)&\mathcal{O}(n^2)&\mathcal{O}(n^2)&\mathcal{O}(n^2)&&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(d(n+r))\\ \text{最好情况}&\mathcal{O}(n^2)&\mathcal{O}(n)&\mathcal{O}(n)&\mathcal{O}(n\operatorname{log}n)&&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(n\operatorname{log}n)&\mathcal{O}(d(n+r))\\ \text{空间复杂度}&\mathcal{O}(1)&\mathcal{O}(1)&\mathcal{O}(1)&\mathcal{O}(n)&\mathcal{O}(1)&\mathcal{O}(1)&\mathcal{O}(n)&\mathcal{O}(r)\\ \text{稳定性}&\text{不稳定}&\text{稳定}&\text{稳定}&\text{不稳定}&\text{不稳定}&\text{不稳定}&\text{稳定}&\text{稳定}\\ \end{matrix} $$
基于比较:通过比较元素来排序数列,如冒泡排序,快速排序等。
不基于比较:不比较元素,通过其他方法(如hash)来进行排序,如基数排序等。
$$\large\texttt{杂项}$$
- OSI模型
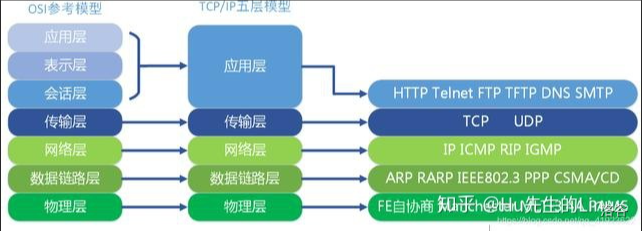
-
IP $\checkmark$
- IPv4:本质上是四个八位二进制数,为了方便表达改为四个十进制数 ,以
.隔开,每一个数字取 $0-255$,例如12.34.56.78。
补:IP 分割成 $4$ 份是为了方便管理。相信大家都听说过洛谷“封IP(段)”这个惩罚,每一位代表着你身处于哪一段。如:需要把
12.34.56.0到12.34.56.255内的 IP 全部封号,只需要封12.34.56.*即可达到操作。- IPv6:八个十六进制数,以
:隔开,主要是防止 IPv4 不够用。
- IPv4:本质上是四个八位二进制数,为了方便表达改为四个十进制数 ,以
-
缩写 $\checkmark$
-
记忆方法:英语好的同学建议记下英文全称,英语不好的话可以记下释义。
-
局域网:LAN(Local Area Network),小范围的网络,$1km$ 以内传输效率极高,结构简单。
-
城域网:MAN(Metropolitan Area Network),数千米至数十千米内。
-
广域网:WAN(Wide Area Network),数十千米至数千千米以上。
-
随机存储器:RAM(Random Access Memory)。
-
只读存储器:ROM(Read Only Memory)。
-
万维网:WWW(World Wide Web)。
-
文件传输协议:FTP(File Transfer Protocol)。
-
简单邮件传输协议:SMTP(Simple Mail Transfer Protocol)。
-
对等网络:P2P(peer-t(w)o-peer),音译。
-
邮局协议第三版 :POP3(Post Office Protocol - Version 3)。
-
传输控制协议:TCP(Transmission Control Protocol)。
-
用户数据报协议:UDP(User Datagram Protocol)。
-
交互邮件访问协议:IMAP(Internet Message Access Protocol)。
-
超文本传输协议:HTTP(S)(Hyper Text Transfer Prtcl(over Securesocket ayer)),带 “S”的为增加了传输加密和身份认证。
-
-
关于 NOIP $\bigstar$
-
NOIP(National Olympiad in Informatics in Provinces),全国青少年信息学奥林匹克联赛(省级),开办于 $1995$ 年,截止 $2018$ 已举办 $24$ 届,$2019$ 年暂停,$2020$ 年恢复。
-
复赛使用 C、C++、Pascal,$2022$ 年后只能使用 C++。
-
复赛使用 NOI Linux 评测。
-
NOI(National Olympiad in Informatics):全国青少年计算机程序设计竞赛,开办于 $1984$ 年,现更名全国青少年信息学奥林匹克竞赛。
-
NOIP(National Olympiad in Informatics in Provinces):全国青少年信息学奥林匹克联赛, 自 $1995$ 年至 $2018$ 年已举办 $24$ 次。复赛可使用 C、C++、Pascal 语言,$2022$ 年后只能使用 C++。 $2019$ 年,由于某种原因, NOIP 暂停 ,在 $2020$ 年恢复。
特别的,如果题目询问了 NOIP 举办了多少届,需要扣除一届,因为 CSP 举行的时候 NOIP 还没有举行。
-
APIO(Asia-Pacific Informatics Olympiad):亚洲与太平洋地区信息学奥林匹克竞赛。
-
IOI(International Olympiad in Informatics):国际信息学奥林匹克竞赛,等级最高的信息学竞赛。
-
-
图片/视频存储与屏幕分辨率 $\bigstar$
-
分辨率:分辨率就是屏幕上显示的像素个数,分辨率 $160\times 128$ 的意思是水平方向含有像素数为 $160$ 个,垂直方向像素数 $128$ 个。屏幕尺寸相同,分辨率越高,显示效果就越精细和细腻。
-
图片存储:给出一张图片的分辨率和色彩的位率(位率越高色彩越多),要算出这张图片所占的空间(一般是 MB)。
计算公式:
$\text{水平方向像素数}\times \text{垂直方向像素数}\times \text{色彩位率}=\text{图片所占空间(Bit)}$
计算完毕后记得转化单位。
例如:某张图片的分辨率为 $1024\times 1024$,是 $24$ 位真彩色,求这张图片占了多少 MB。
$\dfrac{1024\times 1024 \times 24}{1024\times 1024\times 8}=\text{3 MB}$
-
视频大小
一个视频可以视为很多图片的集合,显然,图片的张数为时长乘帧数(每秒几张图片)。
计算公式:
$\text{水平方向像素数}\times \text{垂直方向像素数}\times \text{色彩位率}\times \text{视频时长} \times \text{视频帧数}=\text{视频所占空间(单位:bit)}$
例如:一部 $25$ 帧每秒,$90$ 分钟,分辨率为 $1024\times 768$,$24$ 位真彩色的电影,若没有经过压缩,储存视频信息需要的储存空间大约为?
$\dfrac{1024\times 768\times 24\times 25\times 60\times 90}{1024\times 1024\times 1024\times 8}=296.63085\approx\text{296 GB}$
-
-
操作系统位数 $\checkmark$
-
位数指操作系统所能支配的内存寻址空间,就是该操作系统所能支持的最大内存限制。
-
位数越高,该操作系统支持的数据吞吐量越大:$16$ 位系统最大只能支持 $\text{1 MB}$ 的物理内存地址,$32$ 位最大可以支持 $\text{4 GB}$ 的物理内存地址,$64$ 位最大可以支持 $\text{16384PB}$ 物理内存地址(非常大,远不止 $\text{1 TB}$)。
补:一般来讲,$2006$ 年以后的处理器都是 $64$ 位。
费马小定理:$a^{p-1}\equiv 1\ mod \ p$
$$\large\texttt{参考文献及鸣谢}$$
-
-
参考了部分网络资源以及往期洛谷日报,还有CSP/NOIP的试题。
-
二叉树、栈、队列图片来自OI wiki。
-
补充资料来自百度词条。
-
感谢@xiongyushun @developer6hyx @UnAccepting自动机 @STJqwq(多次) @jpb_Saturn @ppip @x17875487211 的宝贵建议。
$$\tiny \text{(以上排名不分先后)}$$
以上就是 $\text{CSP}\mathbb{\text{初赛知识点梳理}}$ 的全部内容了,如果有问题欢迎在下方留言哦!
$\tiny 2021,\text{洛谷}\ \text{Developed by 159号程序员}$








 浙公网安备 33010602011771号
浙公网安备 33010602011771号