算法设计与分析———分治算法

一、分治法的设计思想

分治法将一个难以直接解决的大问题划分为一些规模较小的子问题，分别求解各个子问题，再合并子问题的解得到原问题的解。

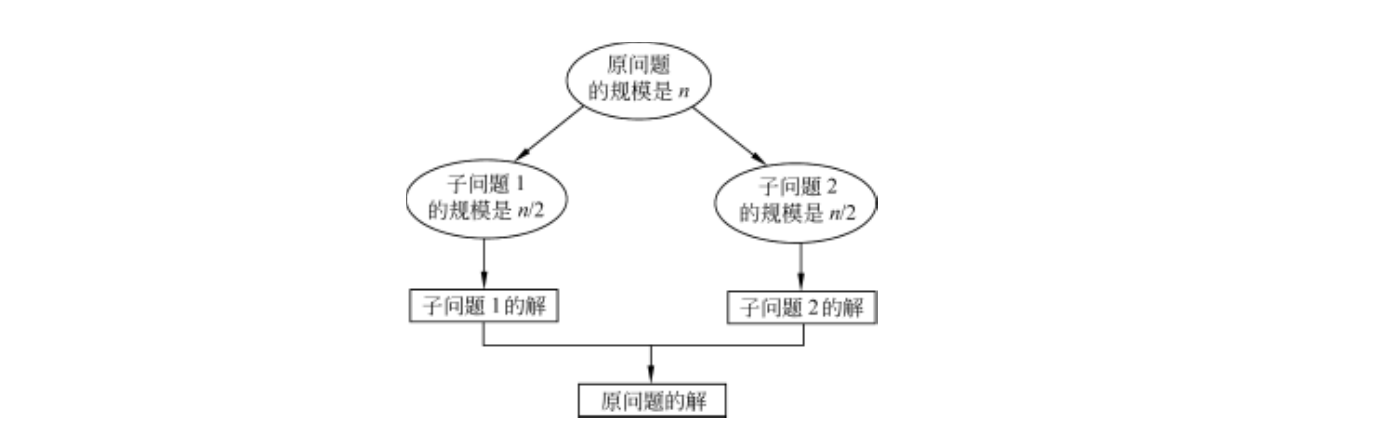
分治法的典型情况

二、分治法的求解过程

一般来说，分治法的求解过程主要由以下三个阶段组成：

1. 划分：吧规模为n的原问题划分为k个规模较小的子问题。
2. 求解子问题：各子问题的解法与原问题的解法通常是相同的，可以用递归或者迭代的方法求解各个子问题，有时递归处理也可以用循环来实现。
3. 合并：把各个子问题的解合并起来，合并的代价因情况不同有很大差异。分治算法的效率很大程度上依赖于合并的实现。

三、几种典型的分治策略算法

• 归并排序

归并排序首先执行划分过程，将序列划分成2个子序列，如果子序列的长度为1，则划分结束，否则，继续执行划分，直到将n个待排序的序列划分为n个长度为1的有序子序列，然后再两两合并，得到⌈n/2⌉个长度为2的有序子序列，再进行两两合并，得到⌈n/4⌉个长度为4的有序子序列，直到得到一个长度为n的有序序列。

代码实现

点击查看代码

void Merge(int r[],int r1[],int s,int m,int t)
{
  int i = s,j = m + 1,k = s;
  while(i <= m && j <= t)
  {
    if(r[i] <= r[j])
       r1[k++] = r[k++];//取r[i]和r[j]中较小的放入r1[k]中
    else
      r1[k++] = r[j++];
  }
  while(i <= m)//若第一个子序列未处理完，则进行收尾处理
    r1[k++] = r[i++];
  while(j <= t)//若第二个子序列未处理完，则进行收尾处理
    r1[k++] = r[j++];
}
void MergeSort(int r[],int s,int t)//对数组r[s]~r[t]进行归并排序
{
  int m,r1[1000];//数组r1为临时数组，假设最多能存1000个元素
  if(s==t) return;
  else
  {
    m = (s+t)/2;//对记录进行划分
    MergeSort(r,s,m);//求解子问题1，归并排序前半个子序列
    MergeSort(r,m+1,t);//求解子问题2,归并排序后半个子序列
    Merge(r,r1,s,m,t);//合并两个有序子序列，将结果存到数组r1中
    for(int i = s;i <= t;i++)//将有序序列传回数组r中
      r[i] = r1[i];
  }
}

该算法的时间复杂度为：O(nlog₂n)

• 快速排序

再待排序表L[1...n]中任取一个元素pivot作为枢轴（通常取首元素），通过一趟排序将待排序表划分成独立的两部分L[1...k-1]和L[k+1...n]，使得L[1...k-1]中的所有元素小于pivot，L[k+1...n]中的所有元素大于等于pivot，，则pivot放在了其最终位置L[k]上，这个过程称为一趟快速排序（一次划分）。对两个子表重复上述过程，直至每部分内只有一个元素或空为止。

代码实现

点击查看代码

int Partition(int r[], int first,int end)//对待排序表进行划分
{
  while(first < end)
  {
    int i = first,j = end;
    while(i < j && r[i] <= r[j]//扫描右侧
          j--;
    if(i < j)
       {
         int temp = r[i];
         r[i] = r[j];
         r[j] = temp;
         i++;
       }
     while(i < j && r[i] <= r[j])//扫描左侧
          i++;
          if(j < j)
          {
            int temp = r[i];
            r[i] = r[j];
            r[j] = temp;
            j--;
          }
  }
    return i;//返回轴值记录的位置
}
void QuickSort(int r[],int firsr,int end)
{
  int pivot;
  if(first < end)
  {
   	pivot = Partition(r,first,end);//划分，pivot是轴值再序列中的位置
    QuickSort(r,first,pivot - 1);//求解子问题1，对左侧子序列进行快速排序
    QuickSort(r,pivot + 1,end);//求解子问题2，对右侧子序列进行快速排序
  }
}
            

该算法的时间复杂度为：O(nlog2n)