5、向量的角度-投影

参考：https://zhuanlan.zhihu.com/p/363627734

向量间的方向可以使用它们之间的夹角表示。我们先看一个线性空间 的例子（2维空间是最简单的多维空间，2维空间的结论基本上都可以推广到多维空间），假设 为两个2维向量，则在2维平面上 可以用两条发自原点的有向线段表示，见下图：

 

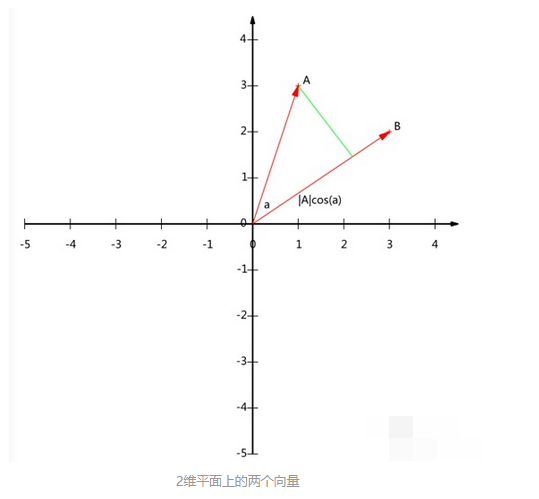
 从 点向 所在直线引一条垂线，垂线与的交点叫作 在 上的投影，再设 与 的夹角是 ，则投影的矢量长度为 ，其中 是向量的模，也就是线段的标量长度。

将向量 的端点连接起来，形成向量O，因此 。在 中，由余弦定理可得:

利用距离公式对这个等式稍作处理，得到

其中 反应了两个向量 之间的角度。而 反应了两个向量的长度，因此

即反应角度又反应长度，因此理所当然地成了内积的定义。我们给两个向量 内积定义一个符号

因此

的内积等于 到 的投影长度乘以 的模。如果 的模是 1 ，则可以看成是一维新的坐标轴上的单位向量，   则是 到 的投影长度，也就是向量 在新坐标轴上的坐标。现在明白规范正交基的价值了吧！

将向量顺便扩展到 维。假设两个向量 ,

则 的内积等于 到 的投影长度乘以 的模。

向量的内积有一些性质：

• 正性
• 定性
• 第一位置加性：对于所有的 都有
• 第一位置齐性：对于所有的 ，都有
• 对称性：对于所有的 ，都有

当线性空间是定义在实数上面时，内积也称为点积。