EvoKG：事件时间和网络结构联合建模的知识图谱推理

摘要

我们如何在时间知识图谱（TKG）上进行知识推理？ TKG 表示有关实体及其关系的事实，其中每个事实都与时间戳相关联。对 TKG 进行推理，即从时间演化的 KG 中推断出新的事实，对于许多应用程序提供智能服务至关重要。然而，尽管可以表示为 TKG 的现实世界数据普遍存在，但大多数方法都侧重于对静态知识图谱的推理，或者无法预测未来事件。在本文中，我们提出了一个problem formulation，将对事件时间和不断演化网络结构进行建模这两个问题同一起来，以便对TKG进行有效推理。我们提出的方法 EvoKG 在一个有效的框架中对这两个任务进行联合建模，该框架通过对事件进行循环建模捕获 TKG 中不断变化的结构和时间动态，并基于时间邻域聚合框架对实体之间的交互进行建模。此外，EvoKG 使用基于神经密度估计的灵活高效机制实现了事件时间的准确建模。实验表明，EvoKG 在有效性（时间和链路预测准确率分别提高 77% 和 116%）和效率方面优于现有方法。

引言

我们如何对随时间不断发展的知识图谱（KGs）进行知识推理？KGs是关于各种类型的实体及其关系的事实的组织和表示。 通过促进以多关系图表示的先验知识的有效使用，KG 为许多重要应用提供支持，包括问答、推荐系统、搜索引擎和自然语言处理。因为KGs通常是不完整的，有许多事实缺失，因此，对KGs的知识推理，即从KGs中的现有事实推断新知识的过程，是这些应用的核心。
重要的是，现实世界中的事件和事实往往与时间有关（即发生在特定时间或在有限时间内有效），表现出实体之间的复杂动态及其随时间演化的关系。这种真实世界的数据（例如ICEW[2]和GDELT[22]）可以建模为时态知识图（TKG），其中实体通过时间戳边连接，两个实体可以在不同的时间步进行多个交互，如图1所示。尽管现实世界中普遍存在可以表示为TKG的数据，但现有方法主要集中于对静态KG的推理，并且缺乏利用TKG中丰富的时间动态的能力。

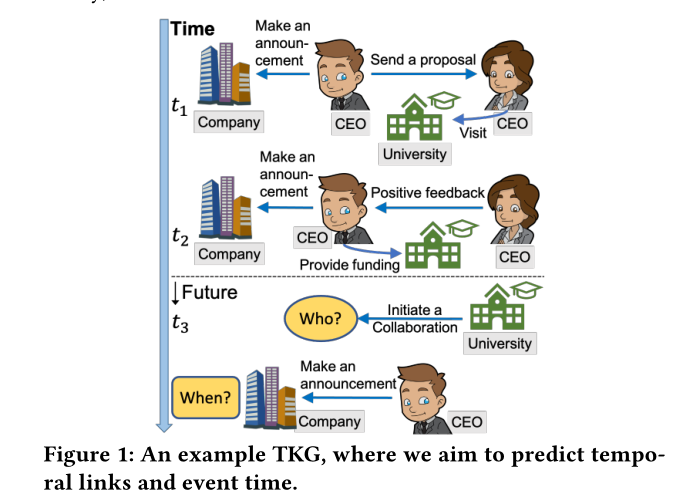
最近，已经研究出来对 TKG 进行推理的方法。 它们主要解决两个问题，即插值和外推。 给定一个从时间 0 到时间 T 的 TKG，插值设置的方法（以HyTE为代表) 可以推断时间 t (0 ≤ t ≤ T ) 的缺失事实； 外推设置 [17, 41, 42] 可以预测时间 t > T 的新事实。在本文中，我们专注于外推设置，它比其他设置更具挑战性和趣味性，作为预测 新兴事件对于 TKG 推理的许多应用非常重要。

在本文中，我们将TKG的联合概率分布定义为条件的乘积来探讨TKG建模问题，从中我们提出了一个问题公式，该公式统一了现有方法的两个问题设置，即建模事件时间和演化网络结构。虽然解决这两个问题可以学习到丰富的、互补的信息，有助于对TKG进行有效推理，但大多数方法只处理这两个问题中的任何一个，如表1所示。

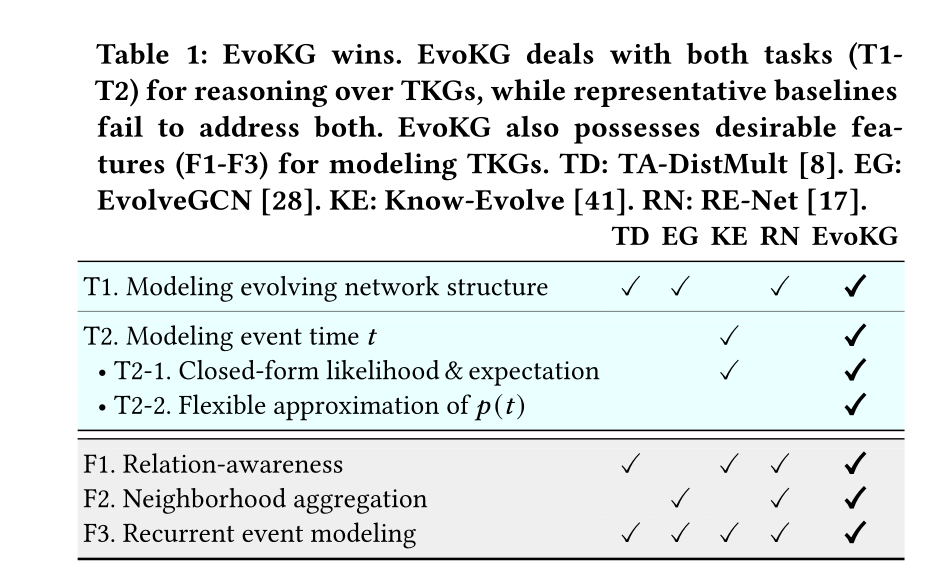
因此，在这项工作中，我们开发了EvoKG，这是一种联合处理TKG推理这两个核心任务的方法。我们设计了一个有效的框架，可以有效地应用于每项任务，只需稍作调整。我们的框架以关系和时间感知的方式执行邻域聚合，并在自回归体系结构中执行重复事件建模，以捕获随时间不断变化的结构和时间动态（表1中的F1-F3）。重要的是，EvoKG利用基于神经密度估计（表1中的T2-1和T2-2）的灵活高效机制，解决了事件时间建模的挑战性任务，避免了现有方法的局限性，即学习的分布不具有表达性，事件时间的对数似然和期望不能以封闭形式获得，而是需要一个近似值。总之，我们的贡献如下：

• problem formulation。我们提出了一个problem formulation，将TKG推理的两个主要任务统一起来——建模事件的时间和演化网络结构
• 框架（第3节）。我们提出了EvoKG，这是一种对TKG进行推理的有效方法，它共同解决了两个核心问题（表1中的T1和T2）。
• 有效性（第4节）。实验表明，与现有的KG推理方法相比，EvoKG的链接和事件时间预测精度分别提高了116%和77%（图2）。
• 效率（第4节）。EvoKG有效地处理并发事件，与现有的最佳方法相比，训练和推理的加速率分别高达30倍和291倍。
  

PROBLEM FORMULATION

符号。时间知识图（TKG）\(G\)是一个具有时间戳边的多关系、有向图。我们用四元组\(（s, r, o, t）\)来表示TKG中带有时间戳的边；它代表在时间\(t\)发生在头实体\(s\)和尾实体\(o\)之间的一个事件，其中边的类型（也称为关系）\(r\)表示相应的事件类型。在TKG中，我们假设没有重复的边，但是如果两个实体有不同的时间戳，它们之间可以有多个相同类型的边。例如，一个TKG可能同时有（'u1', 'emailed', 'u2' '10 am'）和（'u1', 'emailed', 'u2' '12 am'）。

令\((s_n, r_n, o_n, t_n)\) 表示一组有序集合中的第 n 条边。 给定一个TKG \(G\)，其 N 条边按非递减排序时间顺序，我们用\(G = {( (s_n, r_n, o_n, t_n)}_{n=1}^N\) 表示，其中\(0 ≤ t_1 ≤ t_2 ≤ 。 . . ≤ t_N\)。 我们使用\(G_t\)来表示一个由在时间 \(t\) 观察到的事件组成的 TKG，而\(G_{<t}\) 来指代一个包含所有事件的 TKG在时间 \(t\) 之前观察到的事件。 我们使用 \(e\) 来指代事件三元组\((s, r, o)\)。 我们用粗体小写字母（例如 \(\boldsymbol{c}\)）表示向量，和由粗体大写字母组成的矩阵（例如 \(\boldsymbol{W}\)）。
问题：对 TKG 进行建模。给定一个 TKG G 和一系列观察到的事件 {（s， r， o，t）}，我们的目标是对概率分布 p（G） 进行建模。我们假设时间 t 处的事件依赖于在时间 t 之前发生的事件，并且给定先前的事件，同时发生的事件彼此独立。基于这些假设，TKG G 的联合分布可以写为：

\[p(G)=\prod_{t} p\left(G_{t} \mid G_{<t}\right)=\prod_{t} \prod_{(s, r, o, t) \in G_{t}} p\left(s, r, o, t \mid G_{<t}\right) \]

我们进一步分解了联合条件概率\(p\left(s, r, o, t \mid G_{<t}\right)\) 在等式（1）中，如下所示

\[p\left(s, r, o, t \mid G_{<t}\right)=p\left(t \mid s, r, o, G_{<t}\right) \cdot p\left(s, r, o \mid G_{<t}\right) \]

注意，通过对方程（2）中的两项进行建模，我们对事件时间进行了建模\(\left(t \mid s, r, o, G_{<t}\right)\)以及不断演变的网络结构푝\(p\left(s, r, o \mid G_{<t}\right)\). 基于这种分解，我们建议通过估计这两个概率项来建模TKG。
令人惊讶的是，现有的TKG方法侧重于对这两个术语中的任何一个进行建模，但并非同时对这两个术语进行建模，如表1所示。仅解决其中一项任务的方法无法利用通过解决另一项任务可以学到的丰富信息：例如，不建模事件时间的方法（例如，图2中标记为×的方法）无法预测事件何时发生，而仅建模事件时间的方法无法估计事件发生的可能性\((s, r, o)\) 在估计带有时间戳的事件的可能性时要考虑到这一点。通过统一这两个建模任务，我们可以对TKG进行更准确的推理。

MODELING A TEMPORAL KNOWLEDGE GRAPH

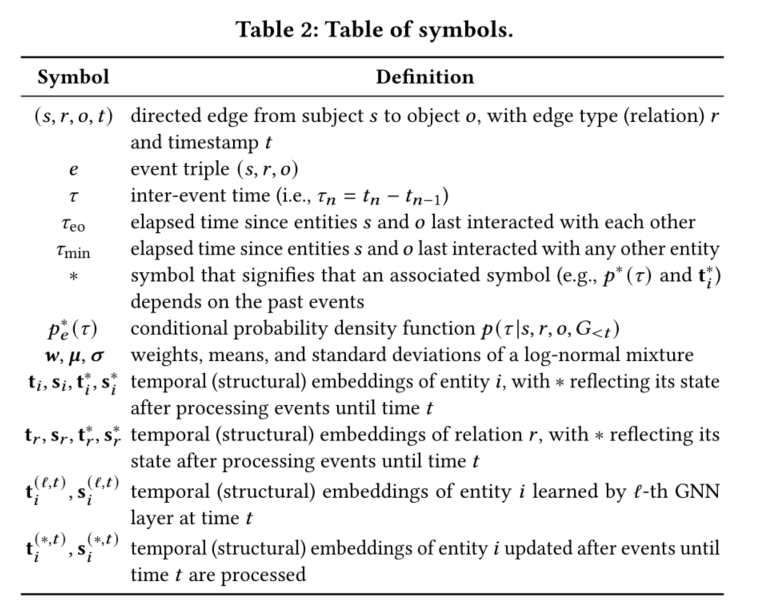
我们描述了EvoKG如何通过解决建模事件时间和演化网络结构这两个问题来建模TKG。表2列出了本文中使用的符号。

Modeling Event Time

TKG中各种类型实体之间发生的事件的时间模式取决于它们过去相互作用的背景。为了捕获现实世界TKGs中存在的错综复杂的时间依赖关系，我们将事件时间\(t\)视为随机变量，并使用时间点过程（TPP）对时间\(t\)处的三元组\(（s，r，o）\)的发生进行建模，TPP是建模不规则间隔发生的事件的主要范例。给定事件时间递增 {. . . ， \(t_{n−1}， t_n\)， . . . }，时间 \(t_n\) 和相应的事件间时间 \(\tau_{n} = t_n − t_{n−1}\) 的表示是相似的的，我们可以互换使用它们。
事件时间的条件密度估计。为了对事件时间进行建模，我们估计事件时间 t 的条件概率密度 \(p_e^*(t) =p\left(t \mid s, r, o, G_{<t}\right)\)，给定实体\(s\)和\(o\)之间的类型为\(r\) 的事件，以及所有过去交互的历史\(G_{<t}\)。请注意，本文中的星号符号∗,例如\(p_e^*(t)\)，表示对历史\(G_{<t}\) 的依赖性。
更准确的说，为了定义\(p_e^*(t)\),我们考虑了两类时间\(\tau_{eo}\)和\(\tau_{min}\)的条件密度。设 \(p_{eo}^*(t) =p\left(\tau_{eo} \mid s, r, o, G_{<t}\right)\)为 \(\tau_{eo}\) 的条件密度，\(\tau_{eo}\)是指实体 s 和 o 在其最新事件中相互交互以来经过的时间。