习题都来自董老师的博客和b站:
这些题目都是优点变形的,不是模版题,需要找到正确使用线段树进行区间维护的方法,再加上一些其他的思想,比如差分、前缀和等,进行区间修改和点修改的转化,修改的时候也可能有不同的情况,比如开方、加上等差数列、sincos的加减等等
涉及到的算法:排序、双指针、贪心、二分、数学、差分、暴力区修、递归合并、离散化、动态开点
线段树+递归合并 Luogu P4198 楼房重建
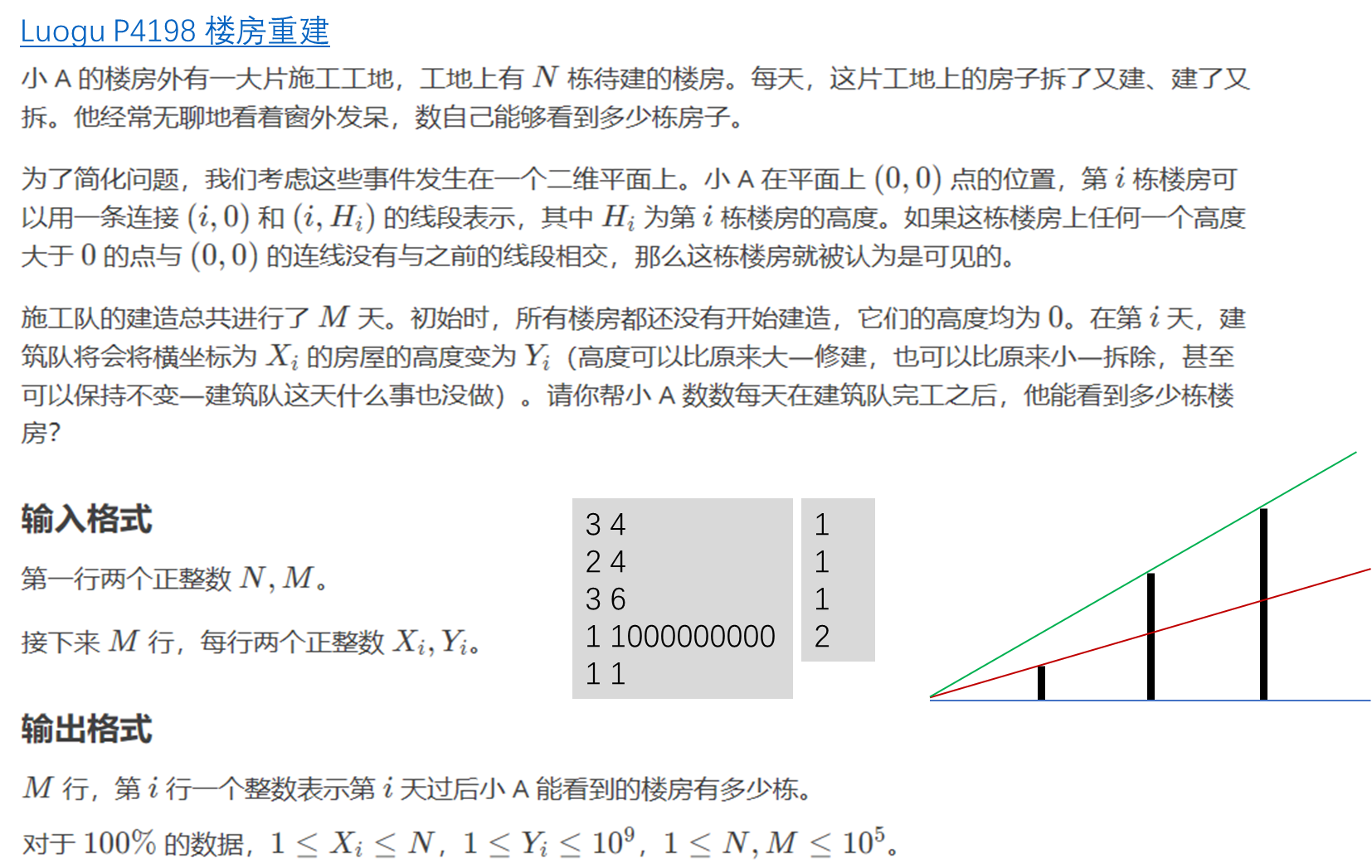
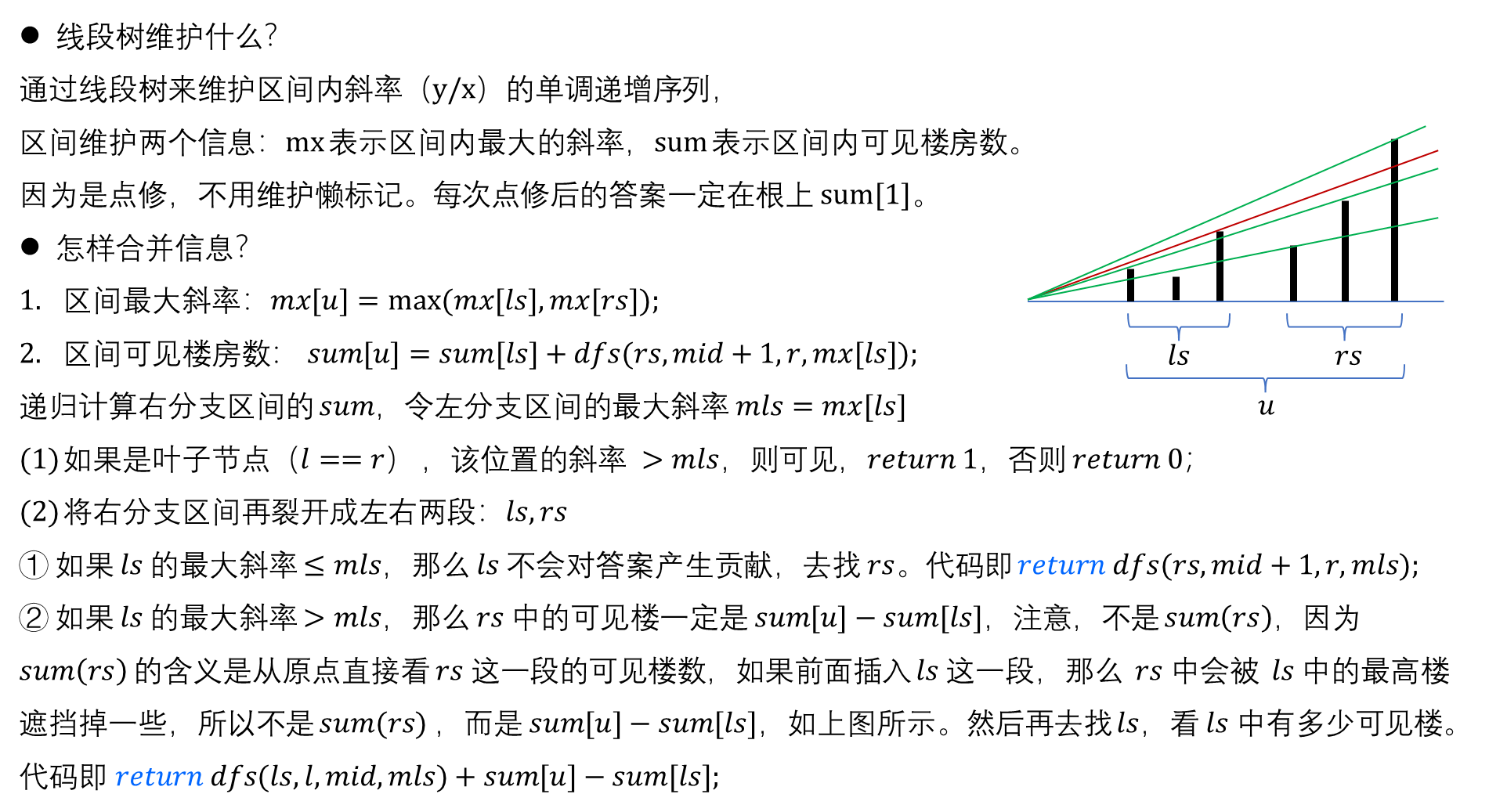
其实这道题的思路肯定是用线段树,但是为了计算结果线段树需要维护哪些信息?
//mx表示区间内的最大斜率,sum表示区间内可见的,主要就是递归求出sum
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstdlib>
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
//其实这道题的思路肯定是用线段树,但是为了计算结果线段树需要维护哪些信息?
//mx表示区间内的最大斜率,sum表示区间内可见的,主要就是递归求出sum
double mx[maxn<<2];
int summ[maxn<<2];
int dfs(int u,int l,int r,double mls){//求右分支sum
if(mx[u]<=mls) return 0; //剪枝
if(l==r) return mx[u]>mls;
if(mx[ls]<=mls) return dfs(rs,mid+1,r,mls);
else return dfs(ls,l,mid,mls)+summ[u]-summ[ls];
}
void pushup(int u,int l,int r){ //上传标记 这个过程中要递归更新值
mx[u]=max(mx[ls],mx[rs]);
summ[u]=summ[ls]+dfs(rs,mid+1,r,mx[ls]); //需要查询
}
void change(int u,int l,int r,int x,double v){ //点修改
if(l==r) {
mx[u]=v;summ[u]=1;return;
}
if(x<=mid) change(ls,l,mid,x,v);
else change(rs,mid+1,r,x,v);
pushup(u,l,r);
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;cin>>x>>y;
change(1,1,n,x,(double)y/x);
cout<<summ[1]<<endl;
}
return 0;
}
线段树+暴力区修 Luogu P4145 上帝造题的七分钟 2


//暴力区间修改,主要是修改的方式不好合并或者打标记
//优化:每个区间维护一个最大值mx,只要mx=1就不用向下分裂了
//每个叶子节点最多修改6次 从12次方到1
//所以综复杂度是6NlogN
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstdlib>
#define LL long long
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
//暴力区间修改,主要是修改的方式不好合并或者打标记
//优化:每个区间维护一个最大值mx,只要mx=1就不用向下分裂了
//每个叶子节点最多修改6次 从12次方到1
//所以综复杂度是6NlogN
LL a[maxn];
LL mx[maxn<<2],summ[maxn<<2];
void pushup(int u){
summ[u]=summ[ls]+summ[rs];
mx[u]=max(mx[ls],mx[rs]);
}
void build(int u,int l,int r){ //建树
summ[u]=mx[u]=a[l];
if(l==r) return;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(u);
}
void change(int u,int l,int r,int x,int y){ //区间修改
if(mx[u]==1) return; //剪枝
if(l==r){
summ[u]=sqrt(summ[u]);
mx[u]=sqrt(mx[u]);
return;
}
if(x<=mid) change(ls,l,mid,x,y);
if(y>mid) change(rs,mid+1,r,x,y);
pushup(u);
}
LL query(int u,int l,int r,int x,int y){ //区间查询
if(x<=l&&r<=y) return summ[u];
LL s=0;
if(x<=mid) s+=query(ls,l,mid,x,y);
if(y>mid) s+=query(rs,mid+1,r,x,y);
return s;
}
int main(){
int n,m,opt,l,r;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
cin>>m;
while(m--){
cin>>opt>>l>>r;
if(l>r) swap(l,r);
if(opt==0){
change(1,1,n,l,r);
}
else cout<<query(1,1,n,l,r)<<endl;
}
return 0;
}
线段树+差分 Luogu P1438 无聊的数列


//差分数组可以将点查询--->区间查询 区间修改--->点修改
//把原数组弄成差分数组,方便加上等差数列
//设差分数列为a,等差数列的首项为s,末项为e,公差为d
//区间[l,r]加上等差数量,等于al+s, al+1~ar +d ar+1-e
//!!对原始序列的点查询--转化为对差分序列的区间查询(前缀和)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstdlib>
#define LL long long
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
//差分数组可以将点查询--->区间查询 区间修改--->点修改
//把原数组弄成差分数组,方便加上等差数列
//设差分数列为a,等差数列的首项为s,末项为e,公差为d
//区间[l,r]加上等差数量,等于al+s, al+1~ar +d ar+1-e
//!!对原始序列的点查询--转化为对差分序列的区间查询(前缀和)
int a[maxn];
LL summ[maxn<<2],tag[maxn<<2]; //懒标记
void pushup(int u){ //上传
summ[u]=summ[ls]+summ[rs];
}
void pushdown(int u,int l,int r){ //下传
summ[ls]+=tag[u]*(mid-l+1);
summ[rs]+=tag[u]*(r-mid); //懒标记下传
tag[ls]+=tag[u];
tag[rs]+=tag[u];
tag[u]=0;
}
void build(int u,int l,int r){
summ[u]=a[l];
tag[u]=0;
if(l==r) return;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(u);
}
void change(int u,int l,int r,int x,int y,LL v){
if(x<=l&&r<=y){
summ[u]+=(r-l+1)*v;
tag[u]+=v;
return;
}
pushdown(u,l,r); //先下传
if(x<=mid) change(ls,l,mid,x,y,v);
if(y>mid) change(rs,mid+1,r,x,y,v);
pushup(u);
}
LL query(int u,int l,int r,int x,int y){
if(x<=l&&r<=y) return summ[u];
pushdown(u,l,r);
LL s=0;
if(x<=mid) s+=query(ls,l,mid,x,y);
if(y>mid) s+=query(rs,mid+1,r,x,y);
return s;
}
int main(){
int n,m,op,l,r,k,d,p;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=n;i>1;i--) a[i]-=a[i-1]; //倒着修改
build(1,1,n) ;//用差分数组建树
for(int i=1;i<=m;i++){
cin>>op;
if(op==1){
cin>>l>>r>>k>>d;
change(1,1,n,l,l,k); //首项修改
if(l+1<=r) change(1,1,n,l+1,r,d) ;//注意要判断范围
if(r<n) change(1,1,n,r+1,r+1,-(k+d*(r-l)));
}
else {
cin>>p;
cout<<query(1,1,n,1,p)<<endl;
}
}
return 0;
}
线段树+差分 Luogu P2184 贪婪大陆

//这个和花神那个是一样的,左右括号法
//前缀和思想:把区间查询转化为前缀和之差
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstdlib>
#define LL long long
#define ls u<<1
#define rs u<<1|1
#define mid ((l+r)>>1)
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
//这个和花神那个是一样的,左右括号法
//前缀和思想:把区间查询转化为前缀和之差
int n,m;
struct node{
int l,r;
int sum[2];
}tr[maxn<<2];
//sum[0]:区间起点数, sum[1]:区间终点数
void pushup(int u,int k){
tr[u].sum[k]=tr[ls].sum[k]+tr[rs].sum[k]; //对应的相加
}
void build(int u,int l,int r){
tr[u]={l,r,0,0};
if(l==r) return ;
build(ls,l,mid);
build(rs,mid+1,r);
}
void change(int u,int x,int k){
if(tr[u].l==tr[u].r){
tr[u].sum[k]++;
return;
}
if(x<=tr[ls].r) change(ls,x,k);
else change(rs,x,k);
pushup(u,k);
}
int query(int u,int x,int y,int k){
if(x>tr[u].r||y<tr[u].l) return 0;
if(x<=tr[u].l&&tr[u].r<=y) return tr[u].sum[k];
return query(ls,x,y,k)+query(rs,x,y,k);
}
int main(){
cin>>n>>m;
build(1,1,n);
for(int i=1;i<=m;i++){
int q,l,r;
cin>>q>>l>>r;
if(q==1) change(1,l,0),change(1,r,1);
else cout<<query(1,1,r,0)-query(1,1,l-1,1)<<endl; //到r的终点数-到l的起点数
}
return 0;
}
线段树+数学 Luogu P6327 区间加区间 sin 和


写代码的时候细节很多,注意
线段树+数学 Luogu P5142 区间方差
点修改,求区间方差,要把方差公式展开,然后数学计算区间和,区间平方和就可以计算了,另外还有乘法逆元


#include<cstdio>
using namespace std;
typedef long long LL;
const int N=100005,mod=1e9+7;
#define ls u<<1
#define rs u<<1|1
#define sqr(x) ((LL)(x)*(x)%mod)
int n,m,a[N];
int L[N<<2],R[N<<2],s1[N<<2],s2[N<<2];
//s1:区间和, s2:区间平方和
int qpow(int a){ //快速幂
int s=1, b=mod-2;
while(b){
if(b&1) s=(LL)s*a%mod;
a=(LL)a*a%mod;
b>>=1;
}
return s;
}
void pushup(int u){ //上传
s1[u]=(s1[ls]+s1[rs])%mod;
s2[u]=(s2[ls]+s2[rs])%mod;
}
void build(int u,int l,int r){ //建树
L[u]=l;R[u]=r;
s1[u]=a[l];s2[u]=sqr(a[l]);
if(l==r) return;
int m=(l+r)>>1;
build(ls,l,m);
build(rs,m+1,r);
pushup(u);
}
void change(int u,int k,int v){ //点修
if(L[u]==R[u]){
s1[u]=v;
s2[u]=sqr(v);
return;
}
int m=(L[u]+R[u])>>1;
if(k<=m) change(ls,k,v);
else change(rs,k,v);
pushup(u);
}
int q1(int u,int x,int y){ //区间和
if(x<=L[u] && R[u]<=y) return s1[u];
int m=(L[u]+R[u])>>1;
int res=0;
if(x<=m) res=q1(ls,x,y);
if(y>m) res=(res+q1(rs,x,y))%mod;
return res;
}
int q2(int u,int x,int y){ //区间平方和
if(x<=L[u] && R[u]<=y) return s2[u];
int m=(L[u]+R[u])>>1;
int res=0;
if(x<=m) res=q2(ls,x,y);
if(y>m) res=(res+q2(rs,x,y))%mod;
return res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1; i<=n; ++i) scanf("%d",&a[i]);
build(1,1,n);
int op,x,y,s1,s2,inv,ave,ans;
while(m--){
scanf("%d%d%d",&op,&x,&y);
if(op==1) change(1,x,y);
else{
s1=q1(1,x,y); //区间和
s2=q2(1,x,y); //区间平方和
inv=qpow(y-x+1); //区间长度的逆元
ave=(LL)s1*inv%mod; //区间算术平均数
ans=(LL)s2*inv%mod-(LL)ave*ave%mod;
ans=(ans%mod+mod)%mod;
printf("%d\n",ans);
}
}
return 0;
}
线段树+二分 Luogu P2824 [HEOI2016/TJOI2016] 排序
C38 线段树+二分 P2824 [HEOI2016/TJOI2016] 排序
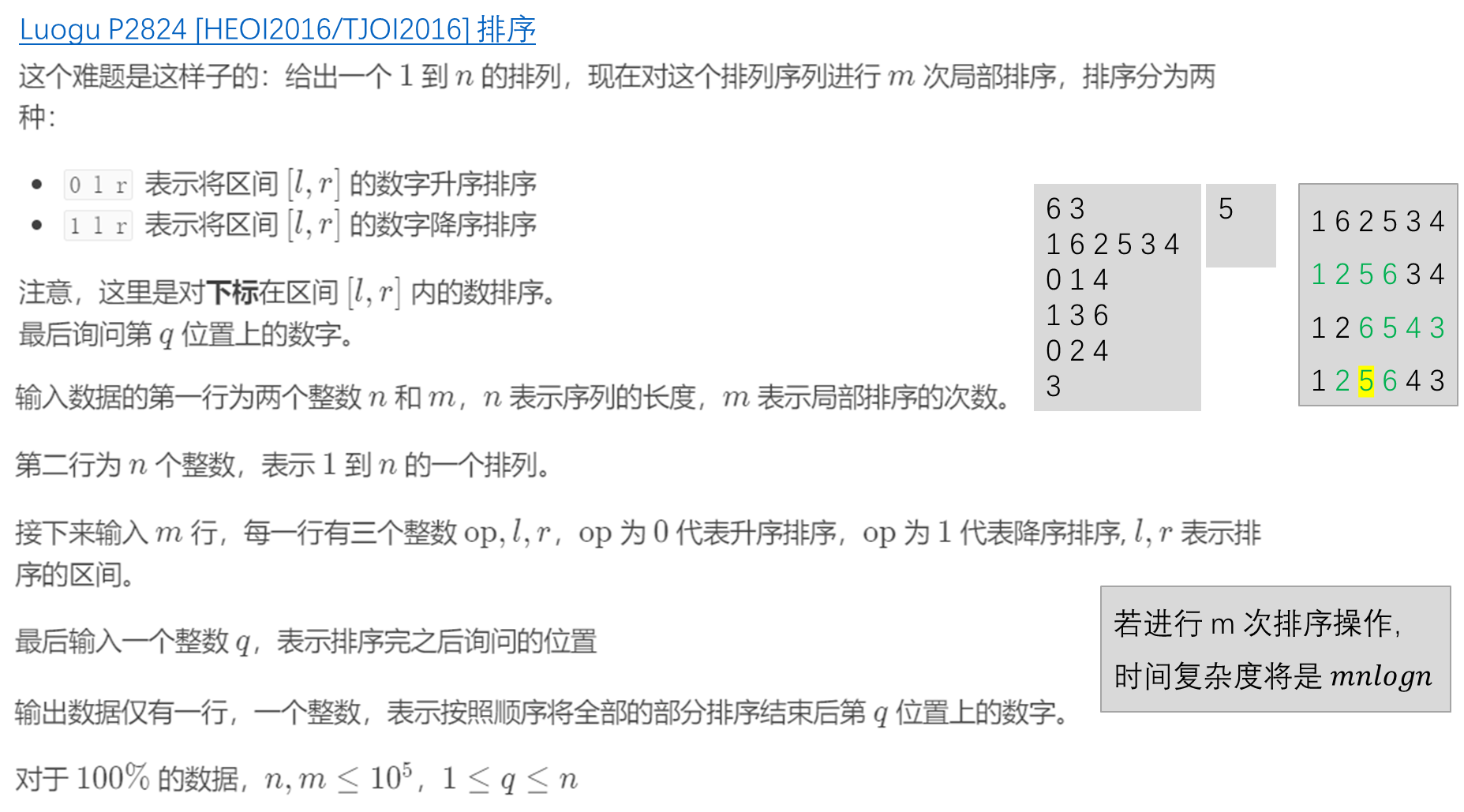

线段树+二分 Luogu P4344 [SHOI2015] 脑洞治疗仪
C37 线段树+二分 P4344 [SHOI2015] 脑洞治疗仪
代码写起真的很多细节
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
#define ls u<<1
#define rs u<<1|1
const int N=200005;
int n,m,opt,l0,r0,l1,r1;
struct tree{
int l,r;
int sum,lmx,rmx,mx;
int len,tag;
}tr[N<<2];
//sum:区间1的个数
//lmx:区间左起0的长度
//rmx:区间右起0的长度
// mx:区间0的最长长度
//len:区间的长度
//tag:区间赋值标记,无标记:-1,有标记:0或1
void pushup(tree& u,tree l,tree r){ //上传
u.sum=l.sum+r.sum;
u.lmx=l.sum ? l.lmx : l.len+r.lmx;
u.rmx=r.sum ? r.rmx : r.len+l.rmx;
u.mx=max(max(l.mx,r.mx),l.rmx+r.lmx);
}
void pd(int u,int k){ //操作区间
tree& t=tr[u];
if(k==0){ //区间赋值为0
t.mx=t.lmx=t.rmx=t.len;
t.sum=0; t.tag=0;
}
else{ //区间赋值为1
t.mx=t.lmx=t.rmx=0;
t.sum=t.len; t.tag=1;
}
}
void pushdown(int u){ //下传
if(tr[u].tag==0) pd(ls,0),pd(rs,0);
if(tr[u].tag==1) pd(ls,1),pd(rs,1);
tr[u].tag=-1;
}
void build(int u,int l,int r){ //建树
tr[u]={l,r,1,0,0,0,r-l+1,-1};
if(l==r) return;
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(tr[u],tr[ls],tr[rs]);
}
void change(int u,int x,int y,int k){ //区修
if(x<=tr[u].l&&tr[u].r<=y){pd(u,k);return;}
pushdown(u);
if(tr[ls].r>=x)change(ls,x,y,k);
if(tr[rs].l<=y)change(rs,x,y,k);
pushup(tr[u],tr[ls],tr[rs]);
}
int q1(int u,int x,int y){ //查询1的个数
if(x<=tr[u].l&&tr[u].r<=y)return tr[u].sum;
pushdown(u);
if(y<tr[rs].l) return q1(ls,x,y);
if(x>tr[ls].r) return q1(rs,x,y);
return q1(ls,x,y)+q1(rs,x,y);
}
int q0(int u,int x,int y){ //查询0的个数
if(x<=tr[u].l&&tr[u].r<=y)
return tr[u].len-tr[u].sum;
pushdown(u);
if(y<tr[rs].l) return q0(ls,x,y);
if(x>tr[ls].r) return q0(rs,x,y);
return q0(ls,x,y)+q0(rs,x,y);
}
void work(){
scanf("%d%d",&l1,&r1);
int x=q1(1,l0,r0); //查询1的个数
if(x==0) return; //去掉会误填1
change(1,l0,r0,0); //全部变成0
int l=l1,r=r1+1; //二分答案
while(l+1<r){
int m=(l+r)>>1;
q0(1,l1,m)<=x ? l=m:r=m;
}
change(1,l1,l,1); //填上1
}
tree query(int u,int x,int y){ //区查
if(x<=tr[u].l&&tr[u].r<=y) return tr[u];
pushdown(u);
if(y<tr[rs].l) return query(ls,x,y);
if(x>tr[ls].r) return query(rs,x,y);
tree T; //开一个临时节点,存储拼凑结果
pushup(T,query(ls,x,y),query(rs,x,y));
return T;
}
int main(){
scanf("%d%d",&n,&m);
build(1,1,n);
while(m--){
scanf("%d%d%d",&opt,&l0,&r0);
if(opt==0) change(1,l0,r0,0);
if(opt==1) work();
if(opt==2) printf("%d\n",query(1,l0,r0).mx);
}
return 0;
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号