后缀树和后缀数组
讲解:
https://www.cnblogs.com/shanchuan04/p/5324009.html
https://blog.csdn.net/yxuanwkeith/article/details/50636898
上面两个参考一下
董老师的视频、《算法竞赛》的代码 hdu 1403
里面的三个数组sa[],rak[],height[],其实应用方面主要使用的是height[]数组,加上根据题目来的check函数,二分答案,得到结果
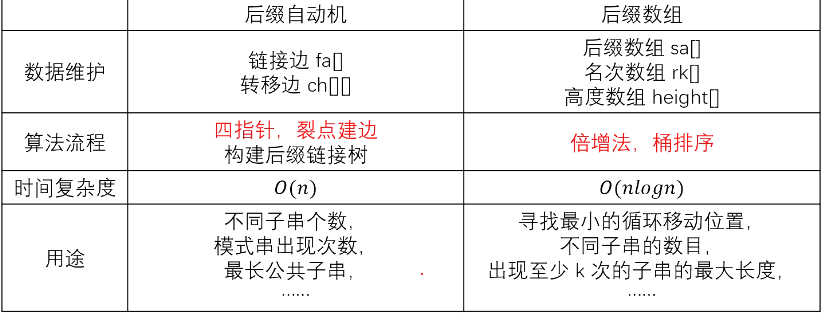
sa[] 后缀数组,sa[i]表示排序为i的后缀编号、rk[i]名次数组,表示后缀i的排名 height[i]高度数组,表示lcp(sa[i],sa[i-1])
1、利用倍增法和桶排序,计算sa数组
倍增法:串的宽度成倍增加,通过偏移量获取桶号 桶排序:同则入桶,不同则加桶。正序存放,逆序拿取
排序过程中先排第二关键字、再排第一关键字,然后就统计桶的个数,达到m=n的时候就可以停止了
2、利用sa[]、rk[]计算出height数组
rk[sa[i]]=i
计算height过程中,利用了定理height[rk[i]]>=height[rk[i-1]]-1 这个定理,可以不用暴力枚举,利用已经计算好的结果,加速新的结果计算
这样while过程中,k的加减不会超过n次,所以最多跑2n次

模板:luogu3809
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=30010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int x[maxn],y[maxn],c[maxn],sa[maxn],rk[maxn],height[maxn];
//x[]是桶数组
char s[maxn];
int n,m;
void get_sa(){
//第一个字母
for(int i=1;i<=n;i++) c[x[i]=s[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1]; //桶
for(int i=n;i;i--) sa[c[x[i]]--]=i; //后缀i的排序是i所在桶号的剩余累计值
//开始基数排序
for(int k=1;k<=n;k<<=1){
//按照第二关键字
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++) y[i]=sa[i]; //辅助数组
for(int i=1;i<=n;i++) c[x[y[i]+k]]++; //偏移量
for(int i=1;i<=m;i++) c[i]+=c[i-1];//向右偏移获取第二关键字的桶号并累计
for(int i=n;i;i--) sa[c[x[y[i]+k]]--]=y[i]; //后续y[i]的排序是第二关键字所在桶号的剩余累计值
//按照第一关键字排序
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++) y[i]=sa[i];
for(int i=1;i<=n;i++) c[x[y[i]]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i;i--) sa[c[x[y[i]]]--]=y[i];//后续y[i]的排序是第一关键字所在桶号的剩余累计值
//把后缀放入桶数组
for(int i=1;i<=n;i++ ) y[i]=x[i];
int i;
//在做新桶,给关键字编桶号,一样放同一个桶,不同放新桶
for(m=0,i=1;i<=n;i++){
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]) x[sa[i]]=m;
else x[sa[i]]=++m;
if(m==n) break;
}
}
}
void get_height(){
for(int i=1;i<=n;i++) rk[sa[i]]=i;
for(int i=1,k=0;i<=n;i++){
if(rk[i]==1) continue;
if(k) k--;
int j=sa[rk[i]-1];
while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) k++;
height[rk[i]]=k;
}
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
m=122;
get_sa();
get_height();
for(int i=1;i<=n;i++) printf("%d ",sa[i]);
return 0;
}
给出两个串,求最长公共子串,和最长重复子串类似,合并s1和s2,得到一个大字符串S,注意中间用‘$’分隔,避免产生更长的子串
首先计算height[]数组,查找最大的height[],然后判断他对应的sa[i]和sa[i-1]对应于大字符串的两端
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define seed 13131
#define maxn 200010
using namespace std;
typedef unsigned long long ull;
char s[maxn];
int sa[maxn],rk[maxn],height[maxn],t1[maxn],cnt[maxn],t2[maxn];
int n;
void calc_sa(){
int m=127;
int i,*x=t1,*y=t2;
for(i=0;i<m;i++) cnt[i]=0;
for(i=0;i<n;i++) cnt[x[i]=s[i]]++;
for(i=1;i<m;i++) cnt[i]+=cnt[i-1];
for(i=n-1;i>=0;i--) sa[--cnt[x[i]]]=i; //
for(int k=1;k<=n;k<<=1){
int p=0;
for(i=n-k;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=k) y[p++]=sa[i]-k;
//
for(i=0;i<m;i++) cnt[i]=0;
for(i=0;i<n;i++) cnt[x[y[i]]]++;
for(i=1;i<m;i++) cnt[i]+=cnt[i-1];
for(i=n-1;i>=0;i--) sa[--cnt[x[y[i]]]]=y[i];
swap(x,y);
p=1;x[sa[0]]=0;
for(i=1;i<n;i++){
x[sa[i]]=y[sa[i]]==y[sa[i-1]]&&y[sa[i-1]+k]==y[sa[i]+k]? p-1:p++;
}
if(p>=n) break;
m=p;
}
}
void get_hei(int n){
int i,j,k=0;
for(i=0;i<n;i++) rk[sa[i]]=i;
for(i=0;i<n;i++){
if(k) k--;
int j=sa[rk[i]-1];
while(s[i+k]==s[j+k]) k++;
height[rk[i]]=k;
}
}
int main(){
int len1,ans;
while(scanf("%s",s)!=EOF){
n=strlen(s);
len1=n;
s[n]='$';
scanf("%s",s+n+1);
n=strlen(s);
calc_sa();
get_hei(n);
ans=0;
// for(int i=0;i<n;i++){
// printf("sa[i]=%d rk[i]=%d\n",sa[i],rk[i]);
// }
// printf("\n");
// for(int i=0;i<n;i++) printf("%d ",height[i]);
for(int i=1;i<n;i++){
if(height[i]>ans&&((sa[i-1]<len1&&sa[i]>=len1)||(sa[i-1]>=len1&&sa[i]<len1))) ans=height[i];
}
printf("%d\n",ans);
}
return 0;
}
一些例题: https://blog.csdn.net/qq_36038511/article/details/78133190
POJ 1743 Musical Theme
不可重叠最长重复子串
题意:有N(1 <= N <=20000)个音符的序列来表示一首乐曲,每个音符都是1..88范围内的整数,现在要找一个重复的主题。“主题”是整个音符序列的一个子串,它需要满足如下条件:
1.长度至少为5个音符。
2.在乐曲中重复出现。(可能经过转调,“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
3.重复出现的同一主题不能有公共部分。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=21010;
const int INF=0x3fffffff;
typedef long long LL;
/*
caioj1467: 后缀数组1:不可重叠最长重复子串
题意:有N(1 <= N <=20000)个音符的序列来表示一首乐曲,每个音符都是1..88范围内的整数,现在要找一个重复的主题。“主题”是整个音符序列的一个子串,它需要满足如下条件:
1.长度至少为5个音符。
2.在乐曲中重复出现。(可能经过转调,“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
3.重复出现的同一主题不能有公共部分。
原文链接:https://blog.csdn.net/qq_36038511/article/details/78133190
*/
int a[maxn],tt[maxn];
char ss[maxn];
int rak[maxn],sa1[maxn],sa2[maxn];
int rsort[maxn];
void get_sa(int n,int m){
memcpy(rak,a,sizeof(rak));
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[i]]--]=i;
int ln=1,p=0;
while(p<n){
int k=0;
for(int i=n-ln+1;i<=n;i++) sa2[++k]=i;
for(int i=1;i<=n;i++) if(sa1[i]-ln>0) sa2[++k]=sa1[i]-ln;
//第二关键字排序
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[sa2[i]]]--]=sa2[i];
for(int i=1;i<=n;i++) tt[i]=rak[i]; //tt辅助数组
p=1;
rak[sa1[1]]=1;
for(int i=2;i<=n;i++){
if(tt[sa1[i]]!=tt[sa1[i-1]]||tt[sa1[i]+ln]!=tt[sa1[i-1]+ln]) p++;
rak[sa1[i]]=p;
}
m=p;
ln*=2;
}
}
//height[i]:sa[i]和sa[i-1]的最长公共前缀的长度
/*
定义h[i]=height[rank[i]],
h数组有以下性质: h[i]≥h[i-1]-1
证明:
(suffix:后缀)
设suffix(k)是排在suffix(i-1)前一名的后缀,则它们的最长公共前缀是h[i-1]。那么同时++,suffix(k+1)将排在suffix(i)的前面(这里一定h[i-1]>1,如果h[i-1]≤1,上面的原式显然成立)并且suffix(k+1)和suffix(i)的最长公共前缀是h[i-1]-1(因为同时往后挪了一位,故-1),所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。因此得证。
实现的时候其实没有必要保存h数组,只须按照h[1],h[2],……,h[n]的顺序计算即可。
*/
int height[maxn*10];
void get_he(int n){ //主要是这个问题
int j,k=0;
for(int i=2;i<=n;i++){
j=sa1[rak[i]-1]; //前一位
if(k!=0) k--; //保证>0
while(a[j+k]==a[i+k]) k++; //暴力询问
height[rak[i]]=k;
}
}
bool check(int k,int n){ //检查有没有重叠
for(int i=2;i<=n;i++){
if(height[i]>=k){
for(int j=i-1;j>=2;j--){
if(abs(sa1[i]-sa1[j])>=k) return 1;
if(height[j]<k) break;
}
}
}
return false;
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
if(n==0) break;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int mmax=-9999999;
for(int i=1;i<n;i++){
a[i]=a[i+1]-a[i]+88;
if(mmax<a[i]) mmax=a[i];
}
a[n]=0;
n--;
get_sa(n,mmax);
get_he(n);
int l=1,r=n,ans=1;
while(l<=r){ //二分答案
int mid=(l+r)/2;
if(check(mid,n)==true){
ans=mid;
l=mid+1;
}
else r=mid-1;
}
if(ans<4) printf("0\n");
else printf("%d\n",ans+1);
}
return 0;
}
后缀数组2:可重叠的k次最长重复子串
【问题描述】
农夫John发现他的奶牛产奶的质量一直在变动。经过细致的调查,他发现:虽然他不能预见明天 产奶的质量,但连续的若干天的质量有很多重叠。我们称之为一个“模式”。 John的牛奶按质量可以被赋予一个0到1000000之间的数。并且John记录了N(1<=N<=20000)天的 牛奶质量值。他想知道最长的出现了至少K(2<=K<=N)次的模式的长度。 比如1 2 3 2 3 2 3 1 中 2 3 2 3出现了两次。当K=2时,这个长度为4。(可重叠的k次最长重复子串)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1100000;
const int INF=0x3fffffff;
typedef long long LL;
/*
caioj1468: 后缀数组2:可重叠的k次最长重复子串
【问题描述】
农夫John发现他的奶牛产奶的质量一直在变动。经过细致的调查,他发现:虽然他不能预见明天 产奶的质量,但连续的若干天的质量有很多重叠。我们称之为一个“模式”。
John的牛奶按质量可以被赋予一个0到1000000之间的数。并且John记录了N(1<=N<=20000)天的 牛奶质量值。他想知道最长的出现了至少K(2<=K<=N)次的模式的长度。 比
如1 2 3 2 3 2 3 1 中 2 3 2 3出现了两次。当K=2时,这个长度为4。(可重叠的k次最长重复子串)
*/
int tt[21000],a[21000],sa1[21000],sa2[21000],rak[21000];
int rsort[maxn],height[21000];
void get_sa(int n,int m){
memcpy(rak,a,sizeof(rak));
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[i]]--]=i;
int ln=1,p=0;
while(p<n){
int k=0;
for(int i=n-ln+1;i<=n;i++) sa2[++k]=i;
for(int i=1;i<=n;i++) if(sa1[i]>ln) sa2[++k]=sa1[i]-ln;
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[sa2[i]]]--]=sa2[i];
memcpy(tt,rak,sizeof(rak));
p=1;
rak[sa1[1]]=1;
for(int i=2;i<=n;i++){
if(tt[sa1[i]]!=tt[sa1[i-1]]||tt[sa1[i]+ln]!=tt[sa1[i-1]+ln]) p++;
rak[sa1[i]]=p;
}
m=p;
ln*=2;
}
}
void get_he(int n){
int j,k=0;
for(int i=1;i<=n;i++){
j=sa1[rak[i]-1];
if(k) k--;
while(a[i+k]==a[j+k]) k++;
height[rak[i]]=k;
}
}
int N,K;
bool check(int x,int n){ //二分检查
int tt=1;
for(int i=2;i<=n;i++){
if(height[i]>=x){
tt++;
if(tt==K) return true;
}
else tt=1;
}
return false;
}
int main(){
while(scanf("%d %d",&N,&K)!=EOF){
int maxx=0;
if(N==0) break;
for(int i=1;i<=N;i++){
scanf("%d",&a[i]);
maxx=max(maxx,a[i]);
}
get_sa(N,maxx);
get_he(N);
int l=1,r=N,ans=0;
while(l<=r){
int mid=(l+r)/2;
if(check(mid,N)) {
ans=mid;
l=mid+1;
}
else r=mid-1;
}
printf("%d\n",ans);
}
return 0;
}
caioj1469: 后缀数组3:连续重复子串
【问题描述】
求两个字符串的最长公共子串。(长度不超过100000)
把两个字符串接在一起,然后在中间插入一个从没有出现过的字符
注意判断找到的公共子串会不会在同一个字符串内
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=510000;
const int INF=0x3fffffff;
typedef long long LL;
//求两个字符串的最长公共子串
//把两个字符串接在一起,然后在中间插入一个从没有出现过的字符
//注意判断找到的公共子串会不会在同一个字符串内
int a[maxn],rak[maxn],rsort[maxn],sa1[maxn],sa2[maxn];
char s1[210000],s2[210000];
int tt[maxn],height[maxn];
void get_sa(int n,int m){
for(int i=1;i<=n;i++) rak[i]=a[i];
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[i]]--]=i;
int p=0,ln=1;
while(p<n){
int k=0;
for(int i=n-ln+1;i<=n;i++) sa2[++k]=i;
for(int i=1;i<=n;i++) if(sa1[i]>ln) sa2[++k]=sa1[i]-ln;
memset(rsort,0,sizeof(rsort));
for(int i=1;i<=n;i++) rsort[rak[i]]++;
for(int i=1;i<=m;i++) rsort[i]+=rsort[i-1];
for(int i=n;i>=1;i--) sa1[rsort[rak[sa2[i]]]--]=sa2[i];
for(int i=1;i<=n;i++) tt[i]=rak[i];
p=1;rak[sa1[1]]=1;
for(int i=2;i<=n;i++){
if(tt[sa1[i]]!=tt[sa1[i-1]]||tt[sa1[i]+ln]!=tt[sa1[i-1]+ln]) p++;
rak[sa1[i]]=p;
}
m=p;
ln*=2;
}
a[0]=0;sa1[0]=0;
}
void get_he(int n){
int k=0;
for(int i=1;i<=n;i++){
int j=sa1[rak[i]-1];
if(k) k--;
while(a[i+k]==a[j+k]) k++;
height[rak[i]]=k;
}
}
int main(){
int n,maxx=0;
scanf("%s",s1+1);
int lena=strlen(s1+1);
scanf("%s",s2+1);
int lenb=strlen(s2+1);
for(int i=1;i<=lena;i++){
a[i]=s1[i];
if(maxx<a[i]) maxx=a[i];
}
a[lena+1]='$';
n=lena+lenb+1;
int pp=0;
for(int i=lena+2;i<=n;i++){
a[i]=s2[++pp];
if(maxx<a[i]) maxx=a[i];
}
get_sa(n,maxx);
get_he(n);
int ans=0;
//能更大,也能保证不在同一个串里面
for(int i=2;i<=n;i++){
if(ans<height[i]&&((sa1[i]<=lena&&sa1[i-1]>lena+1)||(sa1[i]>lena+1&&sa1[i-1]<=lena))) ans=height[i];
}
printf("%d\n",ans);
return 0;
}
caioj1470: 后缀数组4:Life Forms
【问题描述】
求n个字符串(长度1000)的最长的一个子串,满足该子串在一半以上的字符串中出现过,并输出该子串,如果有多个子串满足要求,则按字典序输出所有的子串;
把所有字符串都扔在一起用从未出现过的字符隔开,
然后判断在所有字符串中都出现过的字符串有多少种,
最后输出
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int a[1110000],kinds[1110000],Rank[1110000],Rsort[111000],sa1[1110000],sa2[1110000],tt[1110000],height[1110000];
char s[110000];
void get_sa(int n,int m)
{
for(int i=1;i<=n;i++) Rank[i]=a[i];
memset(Rsort,0,sizeof(Rsort));
for(int i=1;i<=n;i++) Rsort[Rank[i]]++;
for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
for(int i=n;i>=1;i--) sa1[Rsort[Rank[i]]--]=i;
int p=0,ln=1;
while(p<n)
{
int k=0;
for(int i=n-ln+1;i<=n;i++) sa2[++k]=i;
for(int i=1;i<=n;i++) if(sa1[i]-ln>0) sa2[++k]=sa1[i]-ln;
memset(Rsort,0,sizeof(Rsort));
for(int i=1;i<=n;i++) Rsort[Rank[i]]++;
for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
for(int i=n;i>=1;i--) sa1[Rsort[Rank[sa2[i]]]--]=sa2[i];
for(int i=1;i<=n;i++) tt[i]=Rank[i];
p=1;Rank[sa1[1]]=1;
for(int i=2;i<=n;i++)
{
if(tt[sa1[i]]!=tt[sa1[i-1]]||tt[sa1[i]+ln]!=tt[sa1[i-1]+ln]) p++;
Rank[sa1[i]]=p;
}
m=p;ln*=2;
}
a[0]=0;sa1[0]=0;
}
void get_height(int n)
{
int k=0;
for(int i=1;i<=n;i++)
{
int j=sa1[Rank[i]-1];
if(k) k--;
while(a[i+k]==a[j+k]) k++;
height[Rank[i]]=k;
}
}
int stlen=0,v[210],start[1110000];
bool check(int k,int n,int nn)
{
int ks=0,kind=0,stl=0;
for(int i=1;i<=n;i++)
{
if(height[i]<k)
{
if(ks>nn/2)
{
stl++;
start[stl]=sa1[i-1];
}
memset(v,0,sizeof(v));
ks=0;
}
kind=kinds[sa1[i]];
if(v[kind]==0&&kind>0)
{
v[kind]=1;ks++;
}
}
if(ks>nn/2)
{
stlen++;
start[stl]=sa1[n];
}
if(stl) {stlen=stl;return true;}
return false;
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
stlen=0;
if(n==0) break;
int maxx=500,st=0;
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
int len=strlen(s+1);
for(int j=1;j<=len;j++)
{
a[j+st]=s[j];
kinds[j+st]=i;
}
a[len+st+1]=i+400;
kinds[len+st+1]=0;
st+=len+1;
}
get_sa(st,maxx);
get_height(st);
int l=1,r=1100,mid,len=0;
while(l<=r)
{
mid=(l+r)/2;
if(check(mid,st,n))
{
len=mid;l=mid+1;
}
else r=mid-1;
}
for(int i=1;i<=stlen;i++)
{
for(int j=1;j<=len;j++) printf("%c",a[j+start[i]-1]);
printf("\n");
}
if(stlen==0) printf("?\n");
printf("\n");
}
}
一些其他的应用
Q1:一个串中两个串的最大公共前缀是多少?
A1:这不就是Height吗?用rmq预处理,再O(1)查询。
Q2:一个串中可重叠的重复最长子串是多长?
A2:就是求任意两个后缀的最长公共前缀,而任意两个后缀的最长公共前缀都是Height 数组里某一段的最小值,那最长的就是Height中的最大值。
Q3:一个串中不可重叠的重复最长子串是多长?
A3:先二分答案,转化成判别式的问题比较好处理。假设当前需要判别长度为k是否符合要求,只需把排序后的后缀分成若干组,其中每组的后缀之间的Height 值都不小于k,再判断其中有没有不重复的后缀,具体就是看最大的SA值和最小的SA值相差超不超过k,有一组超过的话k就是合法答案。
A4:一个字符串不相等的子串的个数是多少?
Q4:每个子串一定是某个后缀的前缀,那么原问题等价于求所有后缀之间的不相同的前缀的个数。而且可以发现每一个后缀Suffix[SA[i]]的贡献是Len - SA[i] + 1,但是有子串算重复,重复的就是Heigh[i]个与前面相同的前缀,那么减去就可以了。最后,一个后缀Suffix[SA[i]]的贡献就是Len - SA[k] + 1 - Height[k]。
对于后缀数组更多的应用这里就不详细阐述,经过思考后每个人都会发现它的一些不同的用途,它的功能也许比你想象中的更强大!


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号