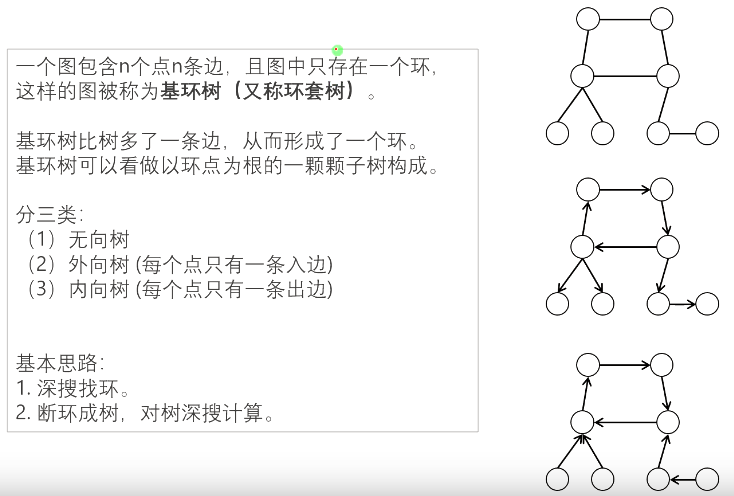
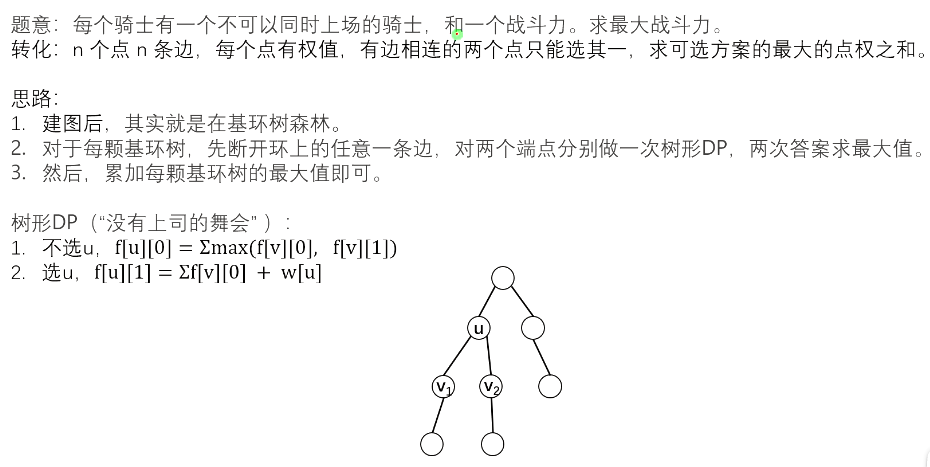
1584:骑士
每个骑士都有讨厌的对象,构成一个环,求最大值(能取的最大战斗力)
#include<queue>
#include<iostream>
#include<algorithm>
typedef long long LL;
#define INF 1e9
using namespace std;
const int maxn=1e6+10;
int n,head[maxn],w[maxn],idx;
LL f[maxn][2],sum;
int r1,r2,vis[maxn];
struct node{
int to,nex;
}e[maxn];
void adde(int x,int y){ //单向边
e[++idx]={y,head[x]};
head[x]=idx;
}
void findd(int x,int rt){ //找出两个根
vis[x]=1;
for(int i=head[x];i;i=e[i].nex){
int v=e[i].to;
if(v==rt) {
r1=x;r2=v;
return;
}
if(vis[v]) continue;
findd(v,rt);
}
}
LL dfs(int u,int rt){
f[u][0]=0;f[u][1]=w[u];
for(int i=head[u];i;i=e[i].nex){
int v=e[i].to;
if(v==rt) continue;
dfs(v,rt);
f[u][0]+=max(f[v][0],f[v][1]);
f[u][1]+=f[v][0];
}
return f[u][0];
}
int main(){
scanf("%d",&n);
for(int v=1,u;v<=n;v++){
scanf("%d %d",&w[v],&u);
adde(u,v);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
r1=r2=0;
findd(i,i);
if(r1){
LL res1=dfs(r1,r1);
LL res2=dfs(r2,r2);
sum+=max(res1,res2);
}
}
}
printf("%lld\n",sum);
return 0;
}
另一种写法:双向边
#include<queue>
#include<iostream>
#include<algorithm>
typedef long long LL;
#define INF 1e9
using namespace std;
const int maxn=1e6+10;
int n,head[maxn],w[maxn],idx=1;
LL f[maxn][2],sum;
int r1,r2,vis[maxn];
struct node{
int to,nex;
}e[maxn<<1]; //双向边
int be[maxn<<1];//双向边
void adde(int x,int y){ //单向边
e[++idx]={y,head[x]};
head[x]=idx;
}
bool findd(int x,int inv){ //找出两个根
vis[x]=1;
for(int i=head[x];i;i=e[i].nex){
if(i==(inv^1)) continue; //是反向边
int v=e[i].to;
if(!vis[v]){
if(findd(v,i)) return 1;
} else{
r1=x;r2=v;be[i]=1;be[i^1]=1; //标记正反向都不能走
return 1;
}
}
return 0;
}
LL dfs(int u,int inv){ //树上dp
vis[u]=1;
f[u][0]=0;f[u][1]=w[u];
for(int i=head[u];i;i=e[i].nex){
int v=e[i].to;
if(be[i]||i==(inv^1)) continue;
dfs(v,i);
f[u][0]+=max(f[v][0],f[v][1]);
f[u][1]+=f[v][0];
}
return f[u][0];
}
int main(){
scanf("%d",&n);
for(int v=1,u;v<=n;v++){
scanf("%d %d",&w[v],&u);
adde(u,v);adde(v,u);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
r1=r2=0;
findd(i,0);
if(r1){
LL res1=dfs(r1,0);
LL res2=dfs(r2,0);
sum+=max(res1,res2);
}
}
}
printf("%lld\n",sum);
return 0;
}
P1399 [NOI2013] 快餐店
T 打算在城市 C 开设一家外送快餐店。送餐到某一个地点的时间与外卖店到该地点之间最短路径长度是成正比的,小 T 希望快餐店的地址选在离最远的顾客距离最近的地方。
快餐店的顾客分布在城市 C 的 NN 个建筑中,这 NN 个建筑通过恰好 NN 条双向道路连接起来,不存在任何两条道路连接了相同的两个建筑。任意两个建筑之间至少存在一条由双向道路连接而成的路径。小 T 的快餐店可以开设在任一建筑中,也可以开设在任意一条道路的某个位置上(该位置与道路两端的建筑的距离不一定是整数)。
现给定城市 C 的地图(道路分布及其长度),请找出最佳的快餐店选址,输出其与最远的顾客之间的距离。
https://www.bilibili.com/video/BV1wN4y1T7S3/?spm_id_from=333.999.0.0&vd_source=23dc8e19d485a6ac47f03f6520fb15c2
董老师的讲解真的好懂!!yyds


优化之后复杂度为O(N)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
typedef long long LL;
using namespace std;
const int maxn=1e5+10;
int n,head[maxn<<1],vis[maxn],fa[maxn],w[maxn],idx;
struct node{
int to,nex,w;
}e[maxn<<1];
int inc[maxn],cv[maxn],cw[maxn],cn; //这是来记录环上的点的,分别是判断点是不是在环上
//环上点编号、环上点权值、点个数
LL d[maxn],A[maxn],B[maxn],C[maxn],D[maxn]; //用来优化第二次dfs的
//A[i]表示 前缀中最大的一条链+当前节点树的最大深度
//B[i]表示前缀中两棵树的最大深度+这两个节点间的距离
LL ans1,ans2=1e8;
void adde(int a,int b,int c){
e[++idx]={b,head[a],c};
head[a]=idx;
}
bool findd(int u){
vis[u]=1;
for(int i=head[u];i;i=e[i].nex){
int v=e[i].to;
if(v!=fa[u]){ //fa这个数组是用来在初次dfs的时候记录环的 也用来避免往回走
fa[v]=u;w[v]=e[i].w; //边权转化为点权
if(!vis[v]){
if(findd(v)) return 1; //找到了就一路返回
}
else{
int p=u;
while(1){
inc[p]=1;cv[++cn]=p;
cw[cn]=w[p];
p=fa[p];if(p==u) break;
}
return 1; //找到了就一路返回
}
}
}
return 0;
}
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nex){
int v=e[i].to,w=e[i].w;
if(!inc[v]&&v!=fa){
dfs(v,u);
ans1=max(ans1,(LL)d[u]+d[v]+w); //枚举没有经过基环的,也就是环上子树内的最大直径
//ans1是所有技术内可以找到的最大直径
d[u]=max(d[u],d[v]+w);
//d[u]是u往下走的最大深度,第二次dfs用得到
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x,y,z;scanf("%d %d %d",&x,&y,&z);
adde(x,y,z);
adde(y,x,z);
}
findd(1);
for(int i=1;i<=cn;i++){
dfs(cv[i],0); //深搜求直径ans1
}
LL summ=0,mx=0;
for(int i=1;i<=cn;i++){ //求前缀
summ+=cw[i-1];
A[i]=max(A[i-1],summ+d[cv[i]]);
B[i]=max(B[i-1],mx+d[cv[i]]+summ);
mx=max(mx,d[cv[i]]-summ);
}
summ=mx=0;
LL cn_1=cw[cn];
cw[cn]=0; //先清空
for(int i=cn;i>=1;--i){
summ+=cw[i];
C[i]=max(C[i+1],summ+d[cv[i]]);
D[i]=max(D[i+1],mx+d[cv[i]]+summ);
mx=max(mx,d[cv[i]]-summ);
}
LL res=0; //这里没赋初值 烦求死
ans2=B[cn]; //断最后一条边
for(int i=1;i<cn;i++){ //凑答案
res=max(max(B[i],D[i+1]),A[i]+C[i+1]+cn_1);
ans2=min(ans2,res); //求 最短的
}
printf("%.1lf",(double)max(ans1,ans2)/2.0);
return 0;
}
P5022 [NOIP2018 提高组] 旅行


董老师讲的很好,特别是运行过程,思路一下子清晰了
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
typedef long long LL;
using namespace std;
const int maxn=5019;
vector<int> g[maxn];
vector<int> path(maxn,maxn); //创建一个大小为maxn的,值也为maxn的序列
int n,m,a,b;
//复杂度O(N^2)
pair<int,int> edge[maxn] ; //记录边,方便断边
int du,dv,vis[maxn];
int cnt,better; //剪枝的
bool dfs(int u){
if(!better){
if(u>path[cnt]) return 1; //一路返回,不用找了,差得很
if(u<path[cnt]) better=-1; // 可以一直往下找,因为这个更好
}
path[cnt++]=u;
vis[u]=1;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(vis[v]) continue;
if(du==u&&dv==v) continue; //遇到断边了
if(du==v&&dv==u) continue;
if(dfs(v)) return 1;
}
return false;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d %d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
edge[i]={a,b};
}
for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end());
if(n==m+1) dfs(1);
else{
for(int i=1;i<=m;i++){
du=edge[i].first;
dv=edge[i].second;
memset(vis,0,sizeof(vis));
cnt=better=0;
dfs(1);
}
}
for(int i=0;i<n;i++) printf("%d ",path[i]);
return 0;
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号