NOIP2009普及组

T3】细胞分裂

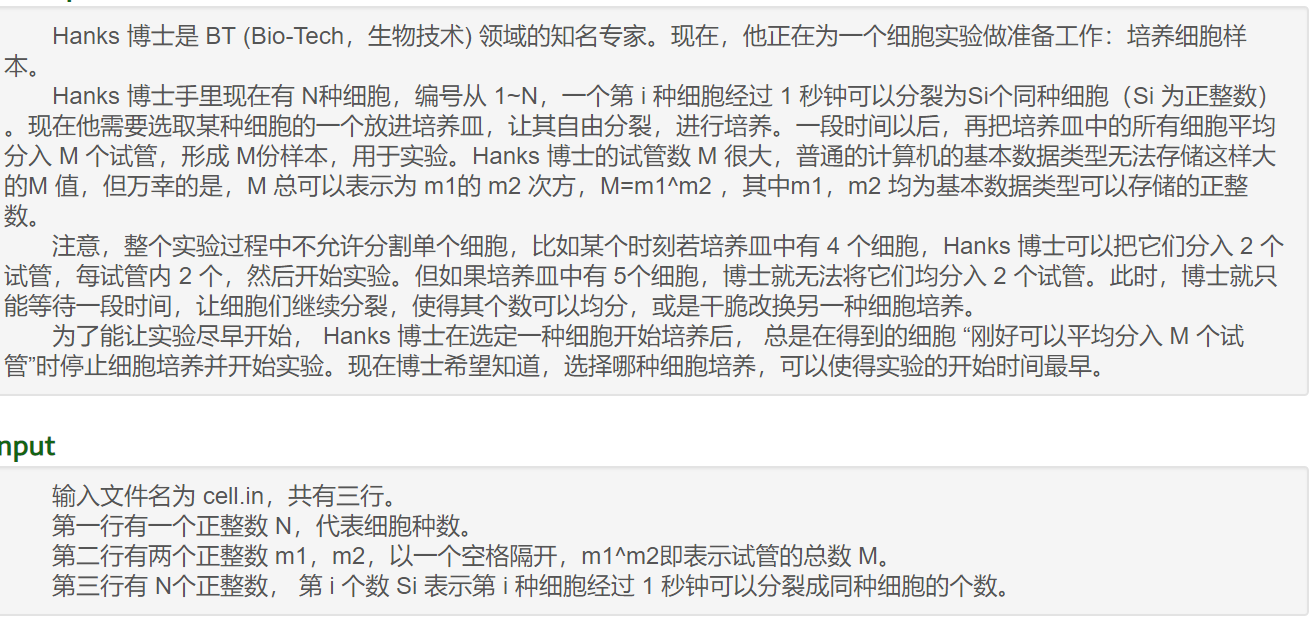
【算法】数论

【题解】均分的本质是A整除B，A整除B等价于A的质因数是B的子集。

1.将m1分解质因数，即m1=p1^a1*p2^a2*...*pk^ak

所以M=m1^m2=p1^(a1*m2)*p2^(a2*m2)*...*pk^(ak*m2)

2.如果s[i](细胞初始个数)不能被M分解出来的质因数（即p1,p2...pn）中的某一个整除的话，这种细胞就永远不可能装入M个瓶子中

换句话说，如果s[i]分解出来的质因数不能包含M的所有质因数的话，就永远不能整除M（即使乘方(分裂)后）。

当然并不需要真的把s[i]分解为质因数，只要有一个s[i]%pj(j=1..k)!=0就说明是-1。

3.确定不是-1后，需要计算最小分裂时间。

当s[i]^ans中包含的每个pi的个数(假设为bi)比M中包含的pi的个数（即ai*m2）多时，就能被M整除。

所以就是找到最小的ans，使每个bi>=(ai*m2)（i=1...n）。

这个ans=ceil(a[i]*m2/b[i]) (只适用于a[i]*m2比b[i]大时)(ceil表示向上取整)

在所有s[i]中寻找最小的ans就是答案。

　　

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
//这是数学题  质因子分解
int m1,m2;
int a[maxn],n,cnt;
int ans=INF;
int b[maxn*3]; 
int js(int x,int y){
	int s=0;
	while(x>0&&x%y==0){
		s++;x/=y;
	}
	return s;
}
int main(){
	cin>>n>>m1>>m2;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=2;i<=m1;i++){  //对m1进行质因子分解 
		while(m1>0&&m1%i==0){
			b[i]++;
			m1/=i;
		}
		b[i]*=m2;
		if(b[i]) cnt++; //质因子个数 
	}
	for(int i=1;i<=n;i++){
		bool flag=1;
		int num=0,res=0;
		for(int j=2;j<=30000;j++){
			if(b[j]){
				if(a[i]%j==0){
					num++;
					int tmp=js(a[i],j);
					res=max(res,(b[j]+tmp-1)/tmp); //后面这个是为了避免小数运算 
				}
				else{
					flag=0;
					break;
				}
			}
			if(num==cnt) break;
		}
		if(flag) ans=min(ans,res);
	}
	if(ans!=INF) cout<<ans<<endl;
	else cout<<"-1"<<endl;
  return 0;
}

　　

T4】道路游戏

 

 

 

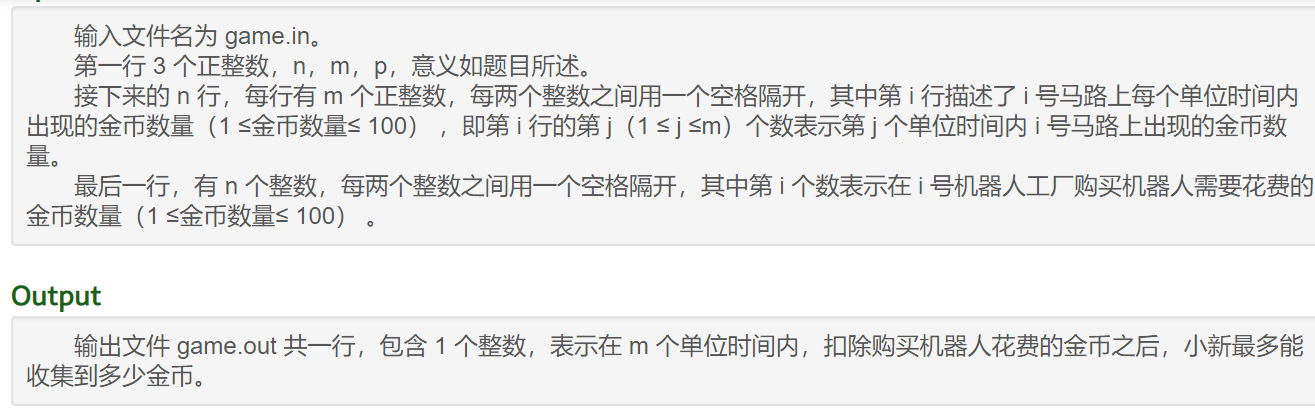
 听起来比较复杂

但是看得出来数据范围不太大，可以试一试暴力，用二维数组存

其实有点像dp,用f[i]表示i这个时刻能够得到的最大值

最外层枚举时间，第二次枚举结尾的地方，第三层枚举走过的时间，就自然得出了出发的地方，在出发的地方买就能得到一个比较的值

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
int cost[maxn];
int value[maxn][maxn]; //地点对应时间出现的价值 
int f[maxn]; //状态压缩至一维的，表示时间i能够取得的最大值，枚举到达结尾和走过的距离k,然后找到最大值 
int n,m,p;
int main(){
	scanf("%d %d %d",&n,&m,&p);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++) scanf("%d",&value[i][j]);
	}
	for(int i=1;i<=n;i++) scanf("%d",&cost[i]);
	memset(f,0x9f,sizeof(f));
	f[0]=0;
	for(int i=1;i<=m;i++){ //时间 
		for(int j=1;j<=n;j++){ //结尾的地点 
			int summ=0; //直接增加枚举从j走到d的值，不用数组存，也不用数组计算，不然太麻烦 
			for(int k=1;k<=p&&k<=i;k++){
				int d=j-k;
				if(d<=0) d=d%n+n;
				summ+=value[d][i-k+1];
				f[i]=max(f[i],f[i-k]+summ-cost[d]); //从d买，然后走k 
			}
		}
	}
	printf("%d\n",f[m]);
return 0;
}