NOIP2015普及组

T1 

金币

 

很简单的题，控制天数这个变量

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=100010;
const int INF=0x3fffffff;
int x;
int main(){
	cin>>x;
	int ans=0,b=0;
	for(int i=1;i<=x;i++){
		for(int j=1;j<=i;j++){
			ans+=i;
			b++;
			if(b>=x) break;
		}
		if(b>=x) break;
	}
	cout<<ans<<endl;
return 0;
}

　　

T3 求和

 

 这道题还是比较好的

涉及公式推理，推理很重要！！！！

https://www.luogu.com.cn/problem/solution/P2671

看着里面的公式推理，其实首先在看到题目的时候就要想如何减小复杂度，找到最优化的方法，这道题首先推理，x+z=2y，那么x+z是偶数，所以x，z同奇或同偶，那么就可以分开处理：把每种颜色分在一起，并且分为奇数位置、偶数位置两组

这里就可以使用数据结构：c[i][2]表示为i这个颜色的奇数位置、偶数位置

然后公式推导开：

(x[1]+x[2])*(y[1]+y[2])+(x[1]+x[3])*(y[1]+y[3])+……+(x[1]+x[k])*(y[1]+y[k])

+(x[2]+x[3])*(y[2]+y[3])+(x[2]+x[4])*(y[2]+y[4])+……+(x[2]+x[k])*(y[2]+y[k])

+…+(x[k-1]+x[k])*(y[k-1]+y[k])=x[1]\*(y[1]+y[2]+y[1]+y[3]+……+y[1]+y[k])+x[2]\*(y[1]+y[2]+y[2]+y[3]+……+y[2]+y[k])+x[k]*(y[1]+y[k]+y[2]+y[k]+……+y[k-1]+y[k])

=x[1]*(y[1]*(n-2)+y[1]+y[2]+……+y[k])+x[2]*(y[2]*(n-2)+y[1]+y[2]+……+y[k])

 

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e5+10;
int s[maxn][2],summ[maxn][2],c[maxn],x[maxn];
//分组：奇数、偶数 
int main(){
 	int n,m;
 	cin>>n>>m;
 	int ans=0;
 	for(int i=1;i<=n;i++){
 		cin>>x[i];
	 }
	 for(int i=1;i<=n;i++){
	 	cin>>c[i];
	 	s[c[i]][i%2]++;
	 	summ[c[i]][i%2]=(summ[c[i]][i%2]+x[i])%10007;
	 }
	for(int i=1;i<=n;i++){
		ans=(ans+i*((s[c[i]][i%2]-2)*x[i]%10007+summ[c[i]][i%2]))%10007;
	}
	cout<<ans<<endl;
  return 0;
}

　　

T4 推销员

 

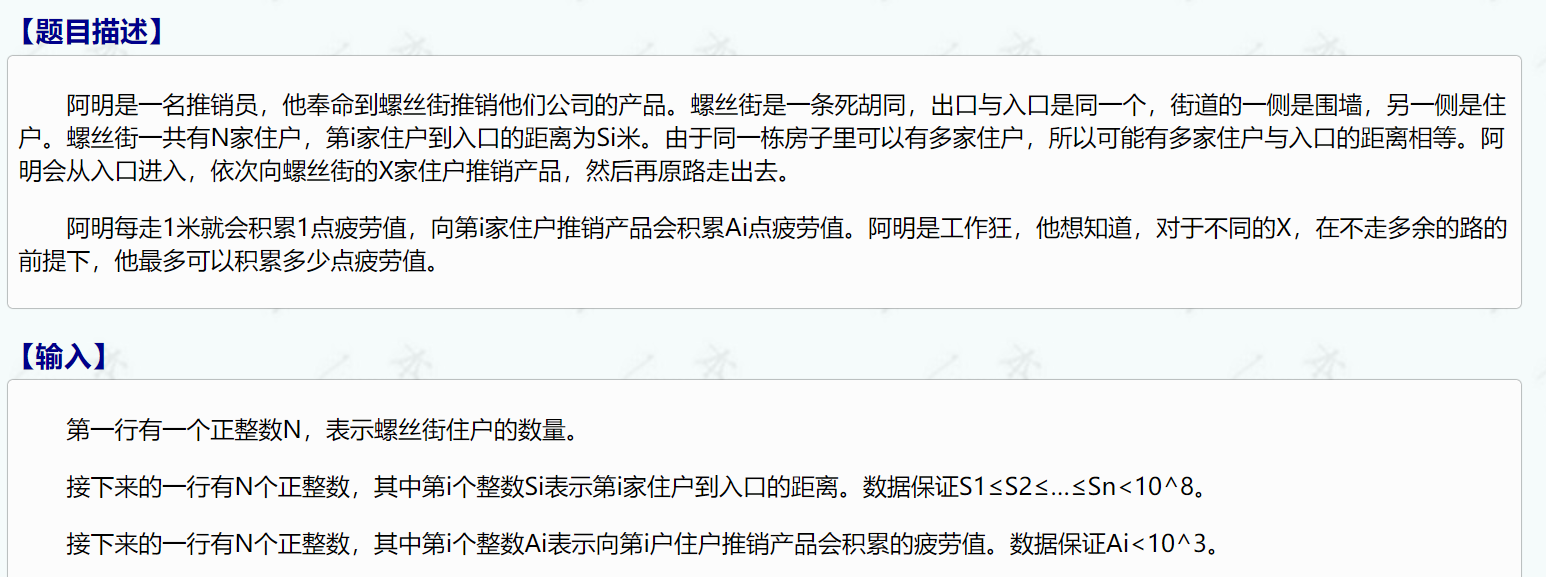
其实这道题就是贪心

https://www.luogu.com.cn/problem/solution/P2672

根据题目的数据范围，也能知道不能暴力或者dp

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e5+10;
int n,summ[maxn],q[maxn],h[maxn]; 
//疲劳前缀和 前i个最大值 后i个最大值 
struct node{
	int s;
	int a;
}op[maxn];
bool cmp(node a,node b){
	return a.a>b.a;
} 
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>op[i].s;
	for(int i=1;i<=n;i++) cin>>op[i].a;
	sort(op+1,op+1+n,cmp);  //按照疲劳程度排序 
	for(int i=1;i<=n;i++){
		summ[i]=summ[i-1]+op[i].a;
	}
	for(int i=1;i<=n;i++) q[i]=max(q[i-1],2*op[i].s);
	for(int i=n;i>=1;i--) h[i]=max(h[i+1],2*op[i].s+op[i].a); //倒着算
	for(int i=1;i<=n;i++) cout<<max(summ[i]+q[i],summ[i-1]+h[i])<<endl; 
	//这个意思就是说要么选现在疲劳值最大的，要么选后面距离和疲劳加起来更大的
	 
  return 0;
}