快速幂
1615:【例 1】序列的第 k 个数
判断等比还是等差--快速幂函数
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int n;
LL k;
int js1(int a,int b){
k-=1;
LL aa=a;
LL temp=b;
while(k){
if(k&1) aa=aa*temp%200907;
temp=temp*temp%200907;
k>>=1;
}
return aa;
}
int js2(int a,int b){
return (a+(k-1)*b)%200907;
}
int main(){
cin>>n;
LL a,b,c;
while(n--){
cin>>a>>b>>c>>k;
if(c-b==b-a){
cout<<js2(a,b-a)<<endl;
}
else if(a!=0){
cout<<js1(a,b/a)<<endl;
}
}
return 0;
}
1616:A 的 B 次方
![]() 直接快速幂
直接快速幂
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
LL a,b,m;
int main(){
cin>>a>>b>>m;
LL temp=a;
LL aa=1;
while(b){
if(b&1) aa=aa*temp%m;
temp=temp*temp%m;
b>>=1;
}
cout<<aa<<endl;
return 0;
}
1617:转圈游戏
![]()
![]()
注意随时取模(对n)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
LL n,m,k,x;
LL solve(LL a,LL b){
LL ans=1;
while(b){
if(b&1) ans=(ans*a)%n;
a=a*a%n;
b>>=1;
}
return ans;
}
int main(){
cin>>n>>m>>k>>x;
m%=n;
cout<<(m*solve(10,k)+x)%n<<endl;
return 0;
}
1618:越狱
监狱有连续编号为n个房间,每个房间关押一个犯人。有 m 种宗教,每个犯人可能信仰其中一种。如果相邻房间的犯人信仰的宗教相同,就可能发生越狱。求有多少种状态可能发生越狱。
每种房间的情况(直接考虑)
总情况数就是 m^n
不会越狱的情况数就是:任意相邻两个都不一样,显然第一个有m中情况,第二个确保不一样就是m-1,第三个和第二个不一样m-1种,类推 所以就是m*m-1^n-1
还有注意看到减法,就有可能越界<0
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
LL m,n;
//总情况数就是 m^n
//不会越狱的情况数就是:任意相邻两个都不一样,显然第一个有m中情况,第二个确保不一样就是m-1,第三个和第二个不一样m-1种,类推 所以就是m*m-1^n-1
LL solve(LL a,LL b){
LL ans=1;
while(b){
if(b&1) ans=(ans*a)%100003;
a=a*a%100003;
b>>=1;
}
return ans;
}
int main(){
cin>>m>>n;
//相减,就要防止越界
cout<<(solve(m,n)-solve(m-1,n-1)*m%100003+100003)%100003;
return 0;
}
质数
线性筛模板:

void prim(){ for(int i=2;i<=n;i++){ if(!vis[i]){ prime[++ans]=i; } for(int j=1;j<=ans&&prime[j]*i<=n;j++){ vis[prime[j]*i]=1; if(i%prime[j]==0) break; } } }
记录最小质因子的模板
void prims(){
memset(v,0,sizeof(v));
int cnt=0;
for(int i=2;i<=n;i++){
if(!v[i]){
v[i]=i;
prim[++cnt]=i;
}
for(int j=1;j<=cnt;j++){
if(prim[j]>v[i]||prim[j]>n/i) break;
v[i*prim[j]]=prim[j];
}
}
for(int i=1;i<=cnt;i++) cout<<prim[i]<<endl;
}
1619: 【例 1】Prime Distance
给定两个整数 L,R,求[L,R] 中相邻两个质数差值最小的数对与差值最大的数对。当存在多个时,输出靠前的素数对。
![]()
这个其实是大区间素数的题目
//埃氏筛法应用于大区间求素数
//1.先用埃氏筛法求出[2,sqrt(b)]区间内的素数,然后用这些素数来筛[a,b]区间的素数即可
本题数据个数不算多,但绝对值很大,逐个判断质数是行不通的,故采用筛选法过滤掉[L,R]内的所有合数。筛选质数有几个可优化之处:
1、任何一个int范围内的合数的最小质因数不超过sqrt(2147483647)=46637,只要能筛掉合数,不需要找出所有质因数,所以,在过滤[L,R]内的合数前可以准备一个质数表。
2、在准备质数表里可以考虑线性筛选,尽量为后面腾出点时间
1、如果L=1,需注意特别处理,因为它不是质数也不是合数,后面算法都过滤不掉,直接令L=2就好(细节)
用质数表过滤[L,R]内的合数时,要考虑是质数本身还是质数的倍数。我们的质数表可以到46637,但L,R也可能较小,会有一倍的时候。
另外,肯定不能直接考虑l-r,所以要把它转移到0-r-l,这个要知道
#include<iostream>
#include<cstring>
using namespace std;
int const N=1e6+5,inf=0x7fffffff;
int a[N],p[N],b[N],c[N],l,r,minn,maxn,l1,r1,l2,r2,cnt,t,n;
void spr()
{
for(int i=2;i<=inf/i;i++)
{
if(!p[i])//i未被标注即为质数
{
p[i]=i;
b[++cnt]=i;
}
for(int j=1;j<=cnt&&p[j]<=p[i]&&i<=inf/i/b[j];j++)
p[i*b[j]]=b[j];
}
}
int main(){
spr();//生成质数表b[N]
while(cin>>l)
{
if(l==1)l=2;
cin>>r;
maxn=0,minn=r;//初始化相邻质数差的最大最小值
l1=l2=r1=r2=0;//差值最小的相邻质数为l1,r1,差值最大的相邻两质数为l2,r2
memset(p,0,sizeof(p));
for(int i=0;i<=r-l;i++)a[i]=l+i;//存入[l,r]间的所有数
for(int i=1;i<=cnt&&b[i]<=r/b[i];i++)//暴力列举所有质因数
{
t=(b[i]-l%b[i])%b[i];//在[l,r]内寻找b[i]的第一个倍数,可能包括b[i]本身
for(int j=t;j<=r-l;j+=b[i])
if(b[i]<a[j])p[j]=1;//标记b[i]的倍数为合数
}
n=0;//统计[l,r]内的质数个数
for(int i=0;i<=r-l;i++)if(!p[i])c[++n]=a[i];
if(n<2)cout<<"There are no adjacent primes.\n";
else
{
t=c[1];
for(int i=2;i<=n;i++)
{
if(minn>c[i]-t)minn=c[i]-t,l1=t,r1=c[i];
if(maxn<c[i]-t)maxn=c[i]-t,l2=t,r2=c[i];
t=c[i];
}
cout<<l1<<","<<r1<<" are closest, "<<l2<<","<<r2<<" are most distant.\n";
}
}
return 0;
}
1620:质因数分解
LL n;
int main(){
cin>>n;
for(LL i=2;i*i<=n;i++){
if(n%i==0){
cout<<n/i<<endl;
break;
}
}
return 0;
}
1621:轻拍牛头

埃氏筛法的思想
/判断一个数是否是另一个数的约数取余就可以了,要计算拍牛的次数,加一个计数器就OK
//用到了筛选法可以优化时间复杂度,那我们也可以考虑用筛选法优化。我们不用把每一个编号都去验证,
//只把当前编号的倍数标记一次。那么每一头牛的编号由原来的验证其余牛的时间复杂度n可降为最大编号值/当前编号值
理解了其实不难
只要存在i,那么就给所有i的倍数都加上这个值
其实这个题的思想也是不直接去按照直接思路走,而是考虑“影响”,因为自己存在,会对自己的倍数造成影响,所以设置三个数组,a[i]表示输入的元素,num[a[i]]表示i存在的次数,所以a[i]所有的倍数ans[j]都加上num[i]
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e6+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int n;
//判断一个数是否是另一个数的约数取余就可以了,要计算拍牛的次数,加一个计数器就OK
//用到了筛选法可以优化时间复杂度,那我们也可以考虑用筛选法优化。我们不用把每一个编号都去验证,
//只把当前编号的倍数标记一次。那么每一头牛的编号由原来的验证其余牛的时间复杂度n可降为最大编号值/当前编号值
int a[maxn];
int num[maxn*10];
int ans[maxn*10];
int main(){
scanf("%d",&n);
int m=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
m=max(m,a[i]);
num[a[i]]++;
}
for(int i=1;i<=m;i++){
if(num[i]){
for(int j=i;j<=m;j+=i) ans[j]+=num[i]; //埃氏筛法的思想
}
}
for(int i=1;i<=n;i++){
printf("%d\n",ans[a[i]]-1);
}
return 0;
}
1622:Goldbach’s Conjecture


欧拉筛出素数后暴力枚举
线性筛----记住这个模板
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1000005;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int n,ans;
int vis[maxn];
int prime[maxn];
//欧拉筛筛出素数后暴力枚举
void prim(){
//线性筛--节约时间
for(int i=2;i<=1000000;i++){
if(!vis[i]){
prime[++ans]=i;
}
for(int j=1;j<=ans&&prime[j]*i<=1000000;j++) {
vis[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
prim();
while(scanf("%d",&n)){
if(n==0) break;
bool flag=0;
for(int i=2;i<=ans&&prime[i]<n;i++){
if(!vis[n-prime[i]]){
flag=1;
printf("%d = %d + %d\n",n,prime[i],n-prime[i]);
break;
}
}
if(flag==0) printf("Goldbach’s conjecture is wrong.\n");
}
return 0;
}
1623:Sherlock and His Girlfriend

其实想通是最难的,只需要分成两类就可以了 最多分成两类,一类质数,一类非质数
有个细节不要忘记了,是需要的质因子,不是因子,所以其实只有两种情况,质数一种颜色,不是质数的一种颜色
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//还是能想到线性筛
int n;
int prime[100005];
int vis[100005];
int ans;
void prim(){
for(int i=2;i<=n;i++){
if(!vis[i]){
prime[++ans]=i;
}
for(int j=1;j<=ans&&prime[j]*i<=n;j++){
vis[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
//需要特判
scanf("%d",&n);
n=n+1;
//只需要分成两类就可以了 最多分成两类,一类质数,一类非质数
if(n==2) printf("1\n1 1\n");
else if(n==3) printf("1\n1 1\n");
else{
prim();
printf("2\n");
for(int i=2;i<=n;i++){
if(vis[i]) printf("2 ");
else printf("1 ");
}
}
return 0;
}
1624:樱花

这道题的推导是真的优点复杂呀
https://www.cnblogs.com/wendcn/p/12626435.html
对本题先试着解一下:x=y*n!/(y-n!)=n!*[y/(y-n!)],由此可得两点:y>n!、y-n!是y*n!的约数,为了方便令y=n!+t,则x=n!*n!/t+n!。显然x的取值个数就是n!*n!的约数个数。接下来就是回顾质因数分解定理了:任何一个大于1的正整数都能唯一分解为有限个质数的乘积。比如:120=2X2X2X3X5。其约数个数的计算方法为:每个质数在约数中出现的个数为0-分解出的个数。比如120可分解为3个2,1个3,1个5的乘积。那约数中可能包含的2的个数分别为0个、1个、2个、3个,共4种(比分解式中2的方次大1——有0个的嘛),其他的一样。故约数个数为(3+1)*(1+1)*(1+1)=16个。若x=a1^n1*a2^n2*a3^n3*......*ak^nk,那么x的约数个数为(n1+1)*(n2+1)*(n3+1)*......*(nk+1)。
n!*n!与n!的质因数应该是一样的,只是个数多了一倍。所以,我们可以转而求n!的质因数个数就好。暴力不行,就筛选。先做一个1-n的质数表,然后找个数。用一个例子来说吧:求100!中7的方次。能出现7的方次,那这个数必然是7的倍数,100!中有7、14、21、28、......、98共14个,其他数不可能有7的方次,那7的方次是14吗?不是。因为49是7的平方,相当于两个7。14个只计算了一次。那再寻找7^2的倍数,2个,在计算7的倍数时也算了他们,只是每个数只计了一次,实际上他们应该记两次,再加一次就好,故7的方次应该是14+2=16。(如果n更大,可能还会有7^3的倍数,每一个应该记三次,前面记了2次,再记一次就好,7的更高方次一样,每升一次方就加一次,直到这个方次超出n)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e6+10;
const int MOD=1e9+7;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//这道题的推导是真的优点复杂呀
//https://www.cnblogs.com/wendcn/p/12626435.html
LL ans=1,a[maxn],p[maxn],b[maxn],n,cnt;
void prim(){
for(int i=2;i<=n;i++){
if(!p[i]){ //未被赋值标记即为质数
p[i]=i;b[++cnt]=i; //质数的最小质因数当然是自己
}
for(int j=1;j<=cnt&&p[j]<=p[i]&&i<=n/b[j];j++) p[i*b[j]]=b[j]; //标记i*b[j]的最小质因数为b[j]
}
}
int main(){
cin>>n;
prim();
for(int i=1;i<=cnt;i++){ //计算每个质数在n!中的方次
LL bs=b[i];
while(bs<=n){
a[i]+=n/bs;
bs*=b[i];
}
}
/*计算n!中bs的倍数个数,每个倍数只记一次,如果是高次方的倍数,分多次计算
比如16!中2的方次,首先所有2的倍数8个,所有4的倍数4个,8的倍数2个,
16的倍数1个,那2的方次为8+4+2+1=15。这与2的奇数倍2 6 10 14共4个记4次,
4的奇数倍2个,每个记2次,共4次,8的奇数倍1个记3次,16的倍数1个记4次,
总计4+4+3+4=15效果一样*/
for(int i=1;i<=cnt;i++)
{
//x的取值个数就是n!*n!的约数个数。 n!*n!与n!的质因数应该是一样的,只是个数多了一倍
ans=ans*(2*a[i]+1);
ans%=MOD;
}
cout<<ans<<endl;
return 0;
}
约数
1625: 【例 1】反素数 Antiprime

![]()
这道题没有想到是用的搜索
质因数分解定理:任何一个大于1的正整数都能唯一分解为有限个质数的乘积。比如:120=2X2X2X3X5。其约数个数的计算方法为:每个质数在约数中出现的个数为0-分解出的个数。
比如120可分解为3个2,1个3,1个5的乘积。那约数中可能包含的2的个数分别为0个、1个、2个、3个,共4种(比分解式中2的方次大1——有0个的嘛),其他的一样。
故约数个数为(3+1)*(1+1)*(1+1)=16个。若x=a1^n1*a2^n2*a3^n3*......*ak^nk,那么x的约数个数为(n1+1)*(n2+1)*(n3+1)*......*(nk+1)。
//题意有点烦,其实就是求不超过n的约数个数最多的最小的数
//可以只用2,3,5,7,11,13,17,19,23,29,31爆搜出这个数
//这个数就是2t1*3t2*5t3*~~~*31t10,且t1>=t2>=t3>=~~~>=t10
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
/*
质因数分解定理了:任何一个大于1的正整数都能唯一分解为有限个质数的乘积。比如:120=2X2X2X3X5。其约数个数的计算方法为:每个质数在约数中出现的个数为0-分解出的个数。
比如120可分解为3个2,1个3,1个5的乘积。那约数中可能包含的2的个数分别为0个、1个、2个、3个,共4种(比分解式中2的方次大1——有0个的嘛),其他的一样。
故约数个数为(3+1)*(1+1)*(1+1)=16个。若x=a1^n1*a2^n2*a3^n3*......*ak^nk,那么x的约数个数为(n1+1)*(n2+1)*(n3+1)*......*(nk+1)。
*/
//题意有点烦,其实就是求不超过n的约数个数最多的最小的数
//可以只用2,3,5,7,11,13,17,19,23,29,31爆搜出这个数
//这个数就是2t1*3t2*5t3*~~~*31t10,且t1>=t2>=t3>=~~~>=t10
LL n;
//不理解
LL num1=0,res1=0;
int prime[]={0,2,3,5,7,11,13,17,19,23,29};
void dfs(int now,LL res,LL num,int up){ //now是当前是那个素数,res是当前的约数个数,num是当前的数大小,up是位数上限(为什么要这个?
if(res>res1){
num1=num;
res1=res;
}
else if(res==res1&&num<num1){
num1=num;
}
for(int i=1;i<=up;i++){
num*=prime[now];
if(num>n) return;
dfs(now+1,res*(i+1),num,i);
}
}
int main(){
cin>>n;
dfs(1,1,1,31);
cout<<num1<<endl;
return 0;
}
1626:【例 2】Hankson 的趣味题

https://www.cnblogs.com/gaojunonly1/p/10428522.html

a=p1^a1*p2^a2*p3^a3.....*pn^an
b=p1^b1*p2^b2*p3^b3....*pn^bn(p1,p2,p3..pn都是质数)
那么gcd(a,b)=p1^min(a1,b1)*p2^min(a2,b2)*p3^min(a3,b3)....*pn^min(an,bn)
lcm(a,b)=p1^max(a1,b1)*p2^max(a2,b2)*p3^max(a3,b3)....*pn^max(an,bn)
那么根据题意就得出:
min(r,t1)=t2 如果t1<t2 无解, 如果t1=t2 r<=t2 ,如果t1>t2 r=t2
max(r,t3)=t4 如果t3<t4 r=t4, 如果t3=t4 r<=t4 ,如果t3>t4 无解
最后可能有一个大于sqrt(b0)的质数因子,没有处理过,所以要特殊判断
/*
原式 b0*x/gcd(b0,x) = b1
-->b0*x = gcd(b0,x)*b1
-->b0*x/b1 = gcd(b0,x)
-->gcd(b0,x) = b0*x/b1
-->gcd(b1/x,b1/b0) = 1
gcd(x,a0)==a1
lcm(x,b0)==b1
//b1一定是x的整倍数,而x一定是a1的整倍数
*/
#include <bits/stdc++.h>
using namespace std;
typedef int ll;
inline ll read()
{
ll s=0;
bool f=0;
char ch=' ';
while(!isdigit(ch))
{
f|=(ch=='-'); ch=getchar();
}
while(isdigit(ch))
{
s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
}
return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
if(x<0)
{
putchar('-'); x=-x;
}
if(x<10)
{
putchar(x+'0'); return;
}
write(x/10);
putchar((x%10)+'0');
return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=50005;
int a0,a1,b0,b1,ans;
bool Bo[N];
int Prim[N];
inline void Pre_Prime()
{
int i,j;
for(i=2;i<=50000;i++)
{
if(!Bo[i]) Prim[++*Prim]=i;
for(j=1;j<=*Prim&&Prim[j]*i<=50000;j++)
{
Bo[Prim[j]*i]=1;
if(i%Prim[j]==0) break;
}
}
return;
}
inline void Solve(int x)
{
int c0=0,c1=0,c2=0,c3=0;
while(a0%x==0){a0/=x; c0++;}
while(a1%x==0){a1/=x; c1++;}
while(b0%x==0){b0/=x; c2++;}
while(b1%x==0){b1/=x; c3++;}
if(c0<c1||c2>c3)
{
ans=0;
return;
}
if(c0==c1&&c2==c3)
{
if(c1<=c3) ans*=c3-c1+1;
else ans=0;
}
else if(c0>c1&&c2<c3&&c1!=c3)
{
ans=0;
}
return;
}
int main()
{
// freopen("son9.in","r",stdin);
// freopen("my.out","w",stdout);
int i,T;
Pre_Prime();
R(T);
while(T--)
{
R(a0); R(a1); R(b0); R(b1);
ans=1;
for(i=1;i<=*Prim&&Prim[i]<b1&&ans;i++)
{
Solve(Prim[i]);
}
if(b1>1) Solve(b1);
Wl(ans);
}
return 0;
}
方法2:
gcd(x,a0)=a1 lcm(x,b0)=b1
则b0*x = b1*gcd(x,b0)
x=b1/b0*gcd(x,b0) 令i=gcd(x,b0) 范围为[1,sqrt(b0)]
判断x=b1/b0*i 和 x=b1/b0*(b0/i)是否满足条件
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
//gcd(x,a0)=a1 lcm(x,b0)=b1
//则b0*x = b1*gcd(x,b0)
//x=b1/b0*gcd(x,b0) 令i=gcd(x,b0) 范围为[1,sqrt(b0)]
//判断x=b1/b0*i 和 x=b1/b0*(b0/i)是否满足条件
int main(){
int n;
int a0,a1,b1,b0;
int ans,x;
cin>>n;
while(n--){
cin>>a0>>a1>>b0>>b1;
ans=0;
for(int i=1;i<sqrt(b0);i++){
if(b0%i==0){
x=b1/b0*i;
if(gcd(x,b0)==i&&gcd(x,a0)==a1) ans++;
x=b1/b0*(b0/i);
if(gcd(x,b0)==b0/i&&gcd(x,a0)==a1) ans++;
}
}
int k=int(sqrt(b0));
if(k*k==b0&&b0%k==0){
x=b1/b0*k;
if(gcd(x,b0)==k&&gcd(x,a0)==a1) ans++;
}
cout<<ans<<endl;
}
return 0;
}
1627:【例 3】最大公约数
![]()
需要用到高精度,另外最大公约数----减法
二进制算法:大整数a,b
如果a,b都是偶数那么为:gcd(a/2,b/2)
如果a,b当中有一个为偶数:gcd(a/2,b)
如果a,b都是奇数:gcd(a-b,b)
对于辗转相减有一个优化,就是对于当前两个数,如果一奇一偶,就把偶数除以2,如果两个偶,就都除以2,把答案*2,如果两奇就辗转相减。
另外有很多重载函数的写法,注意高精度的书写!!
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=3010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//对于辗转相减有一个优化,就是对于当前两个数,如果一奇一偶,就把偶数除以2,如果两个偶,就都除以2,把答案*2,如果两奇就辗转相减。
//https://www.cnblogs.com/gaojunonly1/p/10433546.html
void read_s(char *s){
int len=0;
char ch=' ';
while(!isdigit(ch)) ch=getchar();
while(ch=='0') ch=getchar();
while(isdigit(ch)){
s[++len]=ch;
ch=getchar();
}
return ;
}
char sx[maxn],sy[maxn];
int base=10000,power=4; //倍增?
struct bignum{ //用高精度
int a[maxn];
bignum(){
memset(a,0,sizeof(a));
}
bignum(char *s){
memset(a,0,sizeof(a));
//其实就是1位不存一位数,而是存4位数
int i,bb,pos=0,len=strlen(s+1);
a[0]=(len-1)/power+1;
for(int i=1;i<=len;i++){
if((i-1)%power==0){
//可以存下一位了
bb=1;
pos++;
}
a[pos]+=bb*(s[i]-'0');
bb*=10;
}
}
inline void print(){
printf("%d",a[a[0]]);
int i=1;
for(i=a[0]-1;i>=1;i--){
if(a[i]<1000) printf("0");
if(a[i]<100) printf("0");
if(a[i]<10) printf("0");
printf("%d",a[i]);
}
}
}X,Y;
inline bool operator <(const bignum &p,const bignum &q){
if(p.a[0]!=q.a[0]) return p.a[0]<q.a[0];
for(int i=p.a[0];i>=1;i--){
if(p.a[i]!=q.a[i]) return p.a[i]<q.a[i];
}
return false;
}
inline bool operator ==(const bignum &p,const bignum& q){
if(q.a[0]!=p.a[0]) return false;
for(int i=q.a[0];i>=1;i--){
if(p.a[i]!=q.a[i]) return false;
}
return true;
}
inline bignum operator -(const bignum &p,const bignum &q){
bignum ans=p;
for(int i=1;i<=q.a[0];i++){
ans.a[i]-=q.a[i];
if(ans.a[i]<0){
ans.a[i]+=base;
ans.a[i+1]--;
}
}
//去除开头的0
while((!ans.a[ans.a[0]])&&ans.a[0]) ans.a[0]--;
return ans;
}
inline bignum operator *(const bignum &p,const bignum &q){
bignum ans;
ans.a[0]=max(p.a[0],q.a[0]);
for(int i=1;i<=p.a[0];i++){
for(int j=1;j<=q.a[0];j++){
ans.a[i+j-1]+=p.a[i]*q.a[j];
ans.a[i+j]+=ans.a[i+j-1]/base;
ans.a[i+j-1]%=base;
}
}
while(ans.a[ans.a[0]+1]) ans.a[0]++; //有进位
while(!ans.a[ans.a[0]]) ans.a[0]--; //有前导0
return ans;
}
inline bool judge(bignum p){
if(!p.a[0]) return 1;
return (p.a[1]&1)? 0:1;
}
inline bignum div2(bignum p){
bignum ans;
ans.a[0]=p.a[0];
for(int i=p.a[0];i>=1;i--){
ans.a[i]+=(p.a[i]>>1);
if(p.a[i]&1) p.a[i-1]+=base; //给下一位1个
}
while(!ans.a[ans.a[0]]) ans.a[0]--;
return ans;
}
inline bignum mul2(bignum p){
bignum ans;
ans.a[0]=p.a[0];
for(int i=1;i<=p.a[0];i++){
p.a[i]<<=1;
if(p.a[i]>base){
ans.a[i+1]+=p.a[i]/base;
p.a[i]%=base;
}
ans.a[i]+=p.a[i];
}
while(ans.a[ans.a[0]+1]) ans.a[0]++;
return ans;
}
int main(){
read_s(sx);
reverse(sx+1,sx+strlen(sx+1)+1); //反转这个字符串
X=bignum(sx);
read_s(sy);
reverse(sy+1,sy+strlen(sy+1)+1);
Y=bignum(sy);
bignum ans;
ans.a[0]=ans.a[1]=1;
while(!(X==Y)){
bool is1=judge(X);
bool is2=judge(Y);
if(is1){
if(is2){
X=div2(X);
Y=div2(Y);
ans=mul2(ans);
}
else X=div2(X);
}
else{
if(is2){
Y=div2(Y);
}
else{
bignum p,q;
if(X<Y) p=Y,q=X;
else p=X,q=Y;
X=p-q;
Y=q;
}
}
}
ans=ans*X;
ans.print();
return 0;
}
1628:X-factor Chain
输入正整数 x,x的因子组成的满足任意前一项都能整除后一项的序列的最大长度,以及满足最大长度的序列的个数。
列的最大长度即x的质因子的总个数,而满足最大长度的序列的个数即x的所有质因子的全排列数
//http://www.manongjc.com/detail/11-lbuylmsmdpkiqtd.html
//其实完全可以将这个最长序列的每一项都看成是它的前一项所乘的质数(第一项的前一项可看作是1),那么这样,满足最大长度的序列个数,就是这些质数的不同排列方式的个数,
//即组合数学当中的“不全相异元素的排列”。所以排列数公式为:ans!/(c1!+c2!......+ck!)
前一项能整除后一项, 说明前一项是后一项的因子, 前一项乘以一个数 temp 等于后一项。为了让这个数列尽可能长, 应该让这个 temp 小到不能分解因子。 也就是说, temp是个素数。 因此, 这个题目就转化成了 X 的素因子分解。
数列的不同其实就是乘以各因子的先后顺序不同, 因此最长数列的数量问题就转化成了排列组合问题。注意相同因子的前后顺序不影响数列
首先对X进行素因子分解, 然后求因子全排列的种数, 注意去掉相同因子的干扰。

#include<bits/stdc++.h> using namespace std; #define ll long long const int N=22; ll n,jc[N+1]={1}; inline void solve(int x) { ll ans=0,cnt,k=1; for(ll i=2;i*i<=x;i++) { if(x%i==0) { cnt=0; while(x%i==0) { cnt++; x/=i; }ans+=cnt; k*=jc[cnt]; } } if(x>1) ans++; printf("%lld %lld\n",ans,jc[ans]/k); } int main() { for(int i=1;i<=N;i++) jc[i]=jc[i-1]*i; while(~scanf("%d",&n)) { solve(n); } return 0; }
1629:聪明的燕姿(还是不是很懂)

对于一个数
如果他是p1a1*p1a2*p3a3*~~*pnan
那么他的因数和就是 (p10+p11+p12+...+p1a1)*(p20+p21+...+p2a2)*...*(pn1+pn2+...+pnan)
于是可以爆搜p1~pn及其系数a1~an,随便弄点小剪枝居然就能过了,而且还飞快
剪枝(1),令当前的因数和为S,若(S-1)为质数,那么(S-1)*之前的几个系数显然是一种答案
剪枝(2),令当前的因数和为S,枚举质因数p,若p2>=S,这个p就是非法的,因为就算系数a是1, S除以(p+1)后S也小于p,而之后出现的质因数必须严格大于上一个(没有这个剪枝会T的很惨)
https://www.cnblogs.com/ZH-comld/p/9596448.html
#include<algorithm>
#include<cstring>
#include<iostream>
#include<queue>
typedef long long LL;
using namespace std;
const int maxn=1e5+10; //我们先定p的范围是根号1e5.
int prim[maxn],vis[maxn],s,ans,k,st[maxn],tot;
bool check(int x){
if(x==1) return false;
if(x<=1e5) return !vis[x];
for(int i=1;i<=tot&&(1ll)*prim[i]*prim[i]<=x;i++) if(x%prim[i]==0) return false;
return true;
}
void dfs(int last,int num,int num1){
//last表示搜索到第几个质数,num表示质数和(慢慢变小),num1表示就是最后的结果那个数字
//(p1^0+p1^1+...+p1^a1)*(p2^0+p2^1+...+p2^a2)*...*(pn^0+pn^1+...+pn^an)
if(num==1) {
st[++ans]=num1;return; //搜索到头了
}
if(num-1>prim[last]&&check(num-1)) st[++ans]=(num-1)*num1; //num-1本身就可以
for(int i=last+1;i<=tot&&prim[i]*prim[i]<=num;i++){
for(LL j=prim[i],t=prim[i]+1;t<=num;j*=prim[i],t+=j){
//t 表示就是 p1^0+p1^1+...+p1^a1 这样的式子
if(num%t==0 ) dfs(i,num/t,num1*j);
}
}
}
int main(){
for(int i=2;i<=1e5;i++){
if(!vis[i]){
prim[++tot]=i;
}
for(int j=1;j<=tot&&(k=i*prim[j])<=1e5;j++){
vis[k]=1;
if(i%prim[j]==0) break;
}
}
while(scanf("%d",&s)!=EOF){
ans=0;
dfs(0,s,1);
printf("%d\n",ans);
sort(st+1,st+ans+1);
if(ans){
for(int i=1;i<=ans;i++) printf("%d ",st[i]);
printf("\n");
}
}
return 0;
}
1630:SuperGCD
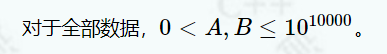
这么大两个数的公约数
于辗转相减有一个优化,就是对于当前两个数,如果一奇一偶,就把偶数除以2,如果两个偶,就都除以2,把答案*2,如果两奇就辗转相减。
//https://www.cnblogs.com/gaojunonly1/p/10433546.html
//方法几乎一样,只是压4位过不去,要压八位,但是最后涉及到乘法需要long long,又会变慢,所以要记录要乘的 2 的个数,在最后统计答案的时候一个个乘进去

#include<iostream> #include<cstring> #include<cmath> #include<algorithm> #include<stack> #include<cstdio> #include<queue> #include<map> #include<vector> #include<set> using namespace std; const int maxn=10010; const int INF=0x3fffffff; typedef long long LL; typedef unsigned long long ull; //对于辗转相减有一个优化,就是对于当前两个数,如果一奇一偶,就把偶数除以2,如果两个偶,就都除以2,把答案*2,如果两奇就辗转相减。 //https://www.cnblogs.com/gaojunonly1/p/10433546.html //方法几乎一样,只是压4位过不去,要压八位,但是最后涉及到乘法需要long long,又会变慢,所以要记录要乘的 2 的个数,在最后统计答案的时候一个个乘进去 void read_s(char *s){ int len=0; char ch=' '; while(!isdigit(ch)) ch=getchar(); while(ch=='0') ch=getchar(); while(isdigit(ch)){ s[++len]=ch; ch=getchar(); } return ; } char sx[maxn],sy[maxn]; int base=100000000,power=8; //倍增? 扩展到8位 struct bignum{ //用高精度 int a[maxn]; bignum(){ memset(a,0,sizeof(a)); } bignum(char *s){ memset(a,0,sizeof(a)); //其实就是1位不存一位数,而是存4位数 int i,bb,pos=0,len=strlen(s+1); a[0]=(len-1)/power+1; for(int i=1;i<=len;i++){ if((i-1)%power==0){ //可以存下一位了 bb=1; pos++; } a[pos]+=bb*(s[i]-'0'); bb*=10; } } inline void print(){ printf("%d",a[a[0]]); int i=1; for(i=a[0]-1;i>=1;i--){ if(a[i]<10000000) printf("0"); if(a[i]<1000000) printf("0"); if(a[i]<100000) printf("0"); if(a[i]<10000) printf("0"); if(a[i]<1000) printf("0"); if(a[i]<100) printf("0"); if(a[i]<10) printf("0"); printf("%d",a[i]); } } }X,Y; inline bool operator <(const bignum &p,const bignum &q){ if(p.a[0]!=q.a[0]) return p.a[0]<q.a[0]; for(int i=p.a[0];i>=1;i--){ if(p.a[i]!=q.a[i]) return p.a[i]<q.a[i]; } return false; } inline bool operator ==(const bignum &p,const bignum& q){ if(q.a[0]!=p.a[0]) return false; for(int i=q.a[0];i>=1;i--){ if(p.a[i]!=q.a[i]) return false; } return true; } inline bignum operator -(const bignum &p,const bignum &q){ bignum ans=p; for(int i=1;i<=q.a[0];i++){ ans.a[i]-=q.a[i]; if(ans.a[i]<0){ ans.a[i]+=base; ans.a[i+1]--; } } //去除开头的0 while((!ans.a[ans.a[0]])&&ans.a[0]) ans.a[0]--; return ans; } inline bignum operator *(const bignum &p,const bignum &q){ bignum ans; ans.a[0]=max(p.a[0],q.a[0]); for(int i=1;i<=p.a[0];i++){ for(int j=1;j<=q.a[0];j++){ ans.a[i+j-1]+=p.a[i]*q.a[j]; ans.a[i+j]+=ans.a[i+j-1]/base; ans.a[i+j-1]%=base; } } while(ans.a[ans.a[0]+1]) ans.a[0]++; //有进位 while(!ans.a[ans.a[0]]) ans.a[0]--; //有前导0 return ans; } inline bool judge(bignum p){ //判断奇偶性 if(!p.a[0]) return 1; return (p.a[1]&1)? 0:1; } inline bignum div2(bignum p){ bignum ans; ans.a[0]=p.a[0]; for(int i=p.a[0];i>=1;i--){ ans.a[i]+=(p.a[i]>>1); if(p.a[i]&1) p.a[i-1]+=base; //给下一位1个 } while(!ans.a[ans.a[0]]) ans.a[0]--; return ans; } inline bignum mul2(bignum p){ bignum ans; ans.a[0]=p.a[0]; for(int i=1;i<=p.a[0];i++){ p.a[i]<<=1; if(p.a[i]>base){ ans.a[i+1]+=p.a[i]/base; p.a[i]%=base; } ans.a[i]+=p.a[i]; } while(ans.a[ans.a[0]+1]) ans.a[0]++; return ans; } int main(){ read_s(sx); reverse(sx+1,sx+strlen(sx+1)+1); //反转这个字符串 X=bignum(sx); read_s(sy); reverse(sy+1,sy+strlen(sy+1)+1); Y=bignum(sy); bignum ans; ans.a[0]=ans.a[1]=1; int op=0; while(!(X==Y)){ bool is1=judge(X); bool is2=judge(Y); if(is1){ if(is2){ X=div2(X); Y=div2(Y); //ans=mul2(ans); op++; } else X=div2(X); } else{ if(is2){ Y=div2(Y); } else{ bignum p,q; if(X<Y) p=Y,q=X; else p=X,q=Y; X=p-q; Y=q; } } } //最后来连乘 for(int i=1;i<=op;i++) X=mul2(X); //ans=ans*X; //ans.print(); X.print(); return 0; }



 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号