1471:【例题1】Phone List
这道题哪里用得着字典树嘛,直接判断,用string的函数不香嘛
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
/*
int t,n,tot;
int tri[maxn][12];
int isend[maxn];
char a[11];
bool insr(char *s){
int now=0,len=strlen(s);
bool xx=0;
for(int i=0;i<len;i++){
int x=s[i]-'0';
if(!tri[now][x]) tri[now][x]=++tot;
now=tri[now][x];
//cout<<now<<" ";
if(isend[now]) xx=1;
}
isend[now]++;
// cout<<endl;
if(xx) return 1;
return 0;
}
bool flag;
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
memset(tri,0,sizeof(tri));
memset(isend,0,sizeof(isend));
flag=0;
while(n--){
scanf("%s",a);
if(insr(a)) flag=1;
}
if(flag) printf("NO\n");
else printf("YES\n");
}
return 0;
}
*/
//我的字典树为什么运行错误!!!!
//不过这道题更见到的做法也很简单了
string ss[10010];
int t,n;
bool flag;
int main(){
cin>>t;
while(t--){
cin>>n;
for(int i=0;i<n;i++) cin>>ss[i];
sort(ss,ss+n);
flag=0;
for(int i=0;i<n-1;i++){
if(ss[i]==ss[i+1].substr(0,ss[i].length())) {
flag=1;
break;
}
}
if(flag) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
1472:【例题2】The XOR Largest Pair
异或的运算、01字典树,学会这类题目
//思路:把每一个数字 x 转化为31位的二进制数,不够的前面补0,并插入到字典树中(最低为二进制位为叶节点);
//接下来对每一个数字 x 的二进制位进行查找,每一步都尽量找与当前位置相反的数字进行访问,入如果有相反的数字,根据xor运算这一位就会留下一个 1 ,最后找出最大值就行。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//思路:把每一个数字 x 转化为31位的二进制数,不够的前面补0,并插入到字典树中(最低为二进制位为叶节点);
//接下来对每一个数字 x 的二进制位进行查找,每一步都尽量找与当前位置相反的数字进行访问,入如果有相反的数字,根据xor运算这一位就会留下一个 1 ,最后找出最大值就行。
int trie[maxn*32][2];
int n,ans;
void inti(){
memset(trie,0,sizeof(trie));
ans=1;
}
void inse(int x){
int now=1;
for(int i=30;i>=0;i--){
int c=x&(1<<i)?1:0;
if(!trie[now][c]){
trie[now][c]=++ans;
}
now=trie[now][c];
}
}
int que(int x){
int now=1;
int tot=0;
for(int i=30;i>=0;i--){
int c=x&(1<<i)?1:0;
if(trie[now][!c]){
now=trie[now][!c];
tot|=(1<<i);
}
else now=trie[now][c];
}
return tot;
}
int main(){
inti();
scanf("%d",&n);
int x,maxx=0;
for(int i=0;i<n;i++){
scanf("%d",&x);
inse(x);
maxx=max(maxx,que(x));
}
printf("%d\n",maxx);
return 0;
}
1473:【例题3】Codechef REBXOR
求两段不相交的连续异或和最大值,就是要处理出异或前缀和,不断加入01Trie树求解即可。
虑到要求两个子段,用ls[i],rs[i分别表示1~i、i~n的最大异或子段,最后扫一遍取max即可。
//原文链接:https://blog.csdn.net/Jason_lxy/article/details/88855100
//重点就是要枚举每一个点左右边的最大异或和
//另一种做法:不太懂 https://blog.csdn.net/bao___zi/article/details/83092217,过不了两个点》。。。。y一个是内存超限,一个是运行错误
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=4e5+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//所以处理出异或前缀和,不断加入01Trie树求解即可。
//考虑到要求两个子段,用ls[i],rs[i分别表示1~i、i~n的最大异或子段,最后扫一遍取max即可。
//原文链接:https://blog.csdn.net/Jason_lxy/article/details/88855100
//重点就是要枚举每一个点左右边的最大异或和
//另一种做法:不太懂 https://blog.csdn.net/bao___zi/article/details/83092217
//过不了两个点》。。。。y一个是内存超限,一个是运行错误
int ch[12500000][2];
int lf[maxn],ri[maxn];
int n,a[maxn];
int tot=1;
inline int read(){
int ret=0,ff=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)){ret=(ret<<3)+(ret<<1)+(ch^48);ch=getchar();}
return ret*ff;
}
inline void inti(){
memset(ch,0,sizeof(ch));
tot=1;
}
inline void inse(int x){
int now=1;
for(int i=30;i>=0;i--){
int c=x&(1<<i)?1:0;
if(!ch[now][c]) ch[now][c]=++tot;
now=ch[now][c];
}
}
inline int fin(int x){
int now=1,ans=0;
for(int i=30;i>=0;i--){
int c=x&(1<<i)?1:0;
if(ch[now][!c]){
now=ch[now][!c];
ans|=(1<<i);
}
else now=ch[now][c];
}
return ans;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
lf[1]=a[1];
inse(a[1]);
for(int i=2;i<=n;i++){
lf[i]=max(lf[i-1],fin(a[i])); //前缀异或和
inse(a[i]);
}
inti();
ri[n]=a[n];
inse(a[n]);
for(int i=n-1;i>=2;i--){
ri[i]=max(ri[i+1],fin(a[i]));
//fin(a[i])表示的其实是通过a[i]异或能够得到的最大值
//而ri[i+1]就是表示不需要用a[i] 去异或
inse(a[i]);
}
int maxx=0;
for(int i=1;i<=n-1;i++){
maxx=max(maxx,lf[i]+ri[i+1]);
}
printf("%d\n",maxx);
return 0;
}
1474:Immediate Decodability
给出一些数字串,判断是否有一个数字串是另一个串的前缀。数字串只包含 0,1,记每个数字串长度为 l,则 1≤l≤10。每组数据至少有 2 个数字串,至多有 8 个数字串。
非常简单,直接和第一问一样,用匹配子串的函数substr就可以了
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
string a[20];
int num;
int main(){
int op=0;
string tmp;
//开始出现的问题是输出超限 因为用了while(1)
while(cin>>tmp){
if(tmp[0]!='9'){
a[++num]=tmp;
continue;
}
if(tmp[0]=='9'){
sort(a+1,a+1+num);
bool flag=0;
for(int i=1;i<=num-1;i++){
if(a[i]==a[i+1].substr(0,a[i].length())) {
flag=1;break;
}
}
if(flag) printf("Set %d is not immediately decodable\n",++op);
else printf("Set %d is immediately decodable\n",++op);
num=0;
}
}
return 0;
}
1475:L语言

【DP】:
首先令f[i]表示到i的前缀能否被理解,那么答案就是f[i]==1时最大的i。
转移也很简单,如果f[i]==1,这个串就可以从i+1开始匹配一个新单词。
f[i+1]|=f[i-len[pos[j]]+1];{f[0]=1;}
【算法】:
1、暴力trie+hash
2、Aho-Corasick Automata(AC自动机全名)
【实现】:
把读入的单词建成一棵Trie树,然后算匹配(可以不用Aho-Corasick,把Trie的查询修改一下也能算),保留从每一个字符开始被匹配的单词长度,然后挨着跑一遍,如果某个字符的前一个字符能够到达,那就把这个字符加上其对应被匹配的长度的位置也标记为能够到达,最后看最末尾的标记就是答案。
https://www.cnblogs.com/shenben/p/6548382.html
还是不太理解
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int N=210;
const int M=1.1e6+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//这个应该是AC字典树??
//https://www.cnblogs.com/shenben/p/6548382.html
/*
把读入的单词建成一棵Trie树,然后算匹配(可以不用Aho-Corasick,把Trie的查询修改一下也能算),保留从每一个字符开始被匹配的单词长度,然后挨着跑一遍
,如果某个字符的前一个字符能够到达,那就把这个字符加上其对应被匹配的长度的位置也标记为能够到达,最后看最末尾的标记就是答案。
*/
int ch[N][27];
int fail[N];
int len[N];
int f[M],q[N];
int pos[N];
int n,m,tot=1;
void insr(string s,int index){
int now=1;
for(int i=0;i<s.length();i++){
int x=s[i]-'a';
if(!ch[now][x]){
ch[now][x]=++tot;
}
now=ch[now][x];
}
pos[now]=index; //这个是在输入的字典中的下标
}
void getfail(){
for(int i=0;i<26;i++) ch[0][i]=1;
int head=0,tail=1,now,p;
q[tail]=1;fail[1]=0;
while(head!=tail){
now=q[++head];
for(int i=0;i<26;i++){
if(!ch[now][i]) continue;
p=fail[now];
while(!ch[p][i]) p=fail[p]; //一直往上,知道找到有这个儿子为止
p=ch[p][i];
fail[ch[now][i]]=p;
q[++tail]=ch[now][i];
}
}
}
int getres(string s){
memset(f,0,sizeof(f));
f[0]=1;
int ans=0;
int now=1;
for(int i=0;i<s.length();i++){
int x=s[i]-'a';
while(!ch[now][x]) now=fail[now];
now=ch[now][x];
//到能够匹配的那一位上去
for(int j=now;j;j=fail[j]){
f[i+1]|=f[i-len[pos[j]]+1];
}
}
for(int i=s.length();~i;i--) {
if(f[i]) {
printf("%d\n",i);break;
}
}
}
int main(){
scanf("%d %d",&n,&m);
string ss;
for(int i=1;i<=n;i++){
cin>>ss;
len[i]=ss.length();
insr(ss,i);
}
fail[0]=0;
getfail();
for(int i=0;i<m;i++){
cin>>ss;
getres(ss);
}
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 20*10+10
#define MAXN 1024*1024+10
using namespace std;
char ch[MAXN];
int n,m,rt=1,cnt=1,trie[maxn][26];
bool use[MAXN],mark[maxn];
inline void insert(int &x,int now,int l)
{
if(!x) x=++cnt;
if(now==l) mark[x]=1;
else insert(trie[x][ch[now]-'a'],now+1,l);
}
inline void find(int x,int now,int l)
{
if(mark[x] && x) use[now]=1; //是单词的结尾
if(!x || now==l) return; //找不到或者是已经找到了
find(trie[x][ch[now]-'a'],now+1,l);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",ch); int l=strlen(ch);
insert(rt,0,l);
}
for(int i=1;i<=m;i++)
{
scanf("%s",ch); int l=strlen(ch);
int ans=0;
memset(use,0,sizeof(use));
use[0]=1;
for(int j=0;j<=l;j++)
if(use[j]) //标记上一位能不能使用过
{
find(rt,j,l);
ans=j;
}
printf("%d\n",ans);
}
}
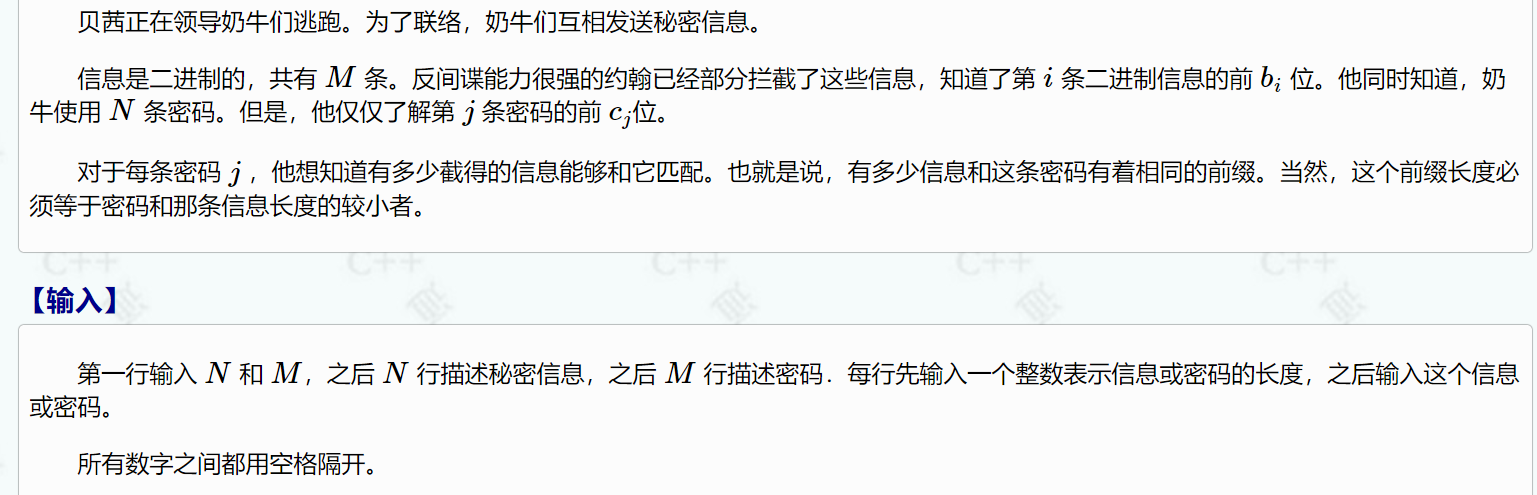
1476:Secret Message 秘密信息
![]()
注意数据范围
这道题也还是AC自动机的问题,但是不用求fail数组,先建立字典树,在建立的过程中维护另一个数组num[maxn][2],其中0表示结尾,1表示有多少个经过
然后再查找每一条密码,在找的过程中加上以当前字符结尾的,找到一半完了直接返回,否则找完了的话再加上(经过的-结尾的)
看代码
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=50010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int ch[maxn*30][2]; //主要是数据开多大的问题
int tot;
int num[maxn*30][2]; //0表示结尾,1表示有多少个经过
//int s[maxn*30];
void inse(string s){
int now=0;
for(int i=0;i<s.length();i++){
int x=s[i]-'0';
if(!ch[now][x]) ch[now][x]=++tot;
now=ch[now][x];
num[now][1]++;
}
num[now][0]++;
}
LL fin(string s){
int now=0;
LL ans=0;
for(int i=0;i<s.length();i++){
int x=s[i]-'0';
if(ch[now][x]==0) return ans; ///如果已经找不到,就返回
//if(i!=s.length()-1) ans+=num[ch[now][x]][0];
//if(i==s.length()-1) ans+=num[ch[now][x]][1];
//cout<<ans<<" ";
now=ch[now][x];
ans+=num[now][0]; //加的是结尾的
}
//cout<<endl;
ans=ans-num[now][0]+num[now][1]; //加上经过的,但是经过的里面多了一个结尾的
return ans;
}
int n,m;
int main(){
scanf("%d %d",&n,&m);
int an,x;
string tmp;
for(int i=0;i<n;i++){
scanf("%d",&an);
tmp="";
while(an--) {
scanf(" %d",&x);tmp+=char(x+'0');
}
inse(tmp);
}
while(m--){
scanf("%d",&an);
tmp="";
while(an--){
scanf("%d",&x);tmp+=char(x+'0');
}
printf("%lld\n",fin(tmp));
}
return 0;
}
1477:【SCOI2016】背单词

贪心+字典树
需要处理以i为跟的子树有多少字符串
后缀比较难处理,那么把 n个单词倒过来,就变成了前缀,所以显然可以把它们倒过来放到trie里。
最优方案一定不能触发第一个条件,因为其它条件的费用加起来一定不会超过n*n。
所以对于一个字符串,如果存在另一个是它的后缀,一定要放在它的前面。
接着考虑按什么顺序放字符串。对于trie上的一条路径,它经过了若干个字符串,这些字符串放的顺序一定是按深度从小到大放的。
然后考虑trie上的一个节点,它可能有多个儿子,那么设size[i]为以i为根的子树有多少个字符串,那么这个先后顺序显然是先把size最小的子树放完,
再放第二小的,一次类推。证明相当于贪心算法的接水问题。
原文链接:https://blog.csdn.net/worldwide_d/article/details/51920189
理解!!
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=510010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//贪心+字典树
/*
需要处理以i为跟的子树有多少字符串
后缀比较难处理,那么把 n个单词倒过来,就变成了前缀,所以显然可以把它们倒过来放到trie里。
最优方案一定不能触发第一个条件,因为其它条件的费用加起来一定不会超过n*n。
所以对于一个字符串,如果存在另一个是它的后缀,一定要放在它的前面。
接着考虑按什么顺序放字符串。对于trie上的一条路径,它经过了若干个字符串,这些字符串放的顺序一定是按深度从小到大放的。
然后考虑trie上的一个节点,它可能有多个儿子,那么设size[i]为以i为根的子树有多少个字符串,那么这个先后顺序显然是先把size最小的子树放完,
再放第二小的,一次类推。证明相当于贪心算法的接水问题。
原文链接:https://blog.csdn.net/worldwide_d/article/details/51920189
*/
int n;
int ch[maxn][26],val[maxn];//以这个为结尾的
int size[maxn]; //下面的字符串个数
int id[maxn]; //dfs序
vector<int> son[maxn];
int dfn,tot=1;
void inse(string s){
int now=1;
int len=s.length();
for(int i=len-1;i>=0;i--){
int x=s[i]-'a';
if(!ch[now][x]) ch[now][x]=++tot;
now=ch[now][x];
}
val[now]++;
}
void build(int fa,int u){ //建树
for(int i=0;i<26;i++){
int pos=ch[u][i];
if(!pos) continue;
if(!val[pos]) build(fa,pos); //如果不是字符串终点
else{
son[fa].push_back(pos);
build(pos,pos);
}
}
}
bool cmp(int x,int y){
return size[x]<size[y];
}
void dfs(int u){ //确定size的值
size[u]=1;
int num=son[u].size();
for(int i=0;i<num;i++){
int t=son[u][i];
dfs(t);
size[u]+=size[t];
}
sort(son[u].begin(),son[u].end(),cmp);
}
LL ans=0;
void solve(int u,int fa){
id[u]=++dfn;
int num=son[u].size();
for(int i=0;i<num;i++){
int t=son[u][i];
solve(t,u);
}
ans+=(LL)id[u]-id[fa];//之间相差的个数
return;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
string s;
cin>>s;
inse(s);
}
build(1,1);
dfs(1);
solve(1,1);
printf("%lld\n",ans);
return 0;
}
1478:The xor-longest Path
给定一棵 n 个点的带权树,求树上最长的异或和路径。
第一行一个整数 n,接下来 n−1 行每行三个整数 u,v,w,表示 u,v 之间有一条长度为 w 的边。

这样的转变就能让解题变得很简单
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#define MAXN 112222
#define MAXM 3122222 //QAQ!!!!
using namespace std;
int tot,s,head[MAXN];
struct node1{
int v,w,next;
}edge[MAXN*2];//因为双向边,所以*2
struct node2{
int ch[3];
}tr[MAXM];//字典树
void addedge(int ui,int vi,int wi)//邻接表加边
{
edge[tot].v=vi;
edge[tot].w=wi;
edge[tot].next=head[ui];
head[ui]=tot++;
edge[tot].v=ui;
edge[tot].w=wi;
edge[tot].next=head[vi];
head[vi]=tot++;
}
int n,ans,flag[MAXN],val[MAXN];
void dfs(int x,int l)//dfs求出val[i]
{
val[x]=l;
flag[x]=1;
for (int i=head[x];i!=0;i=edge[i].next)
{
int vv=edge[i].v;
int ww=edge[i].w;
if (flag[vv]!=1)
dfs(vv,l^ww);
}
}
void newnode(int x,int tmp)
//在字典树上开新点,这是种比较麻烦的写法,还有一种更加简捷的方法自行查询
{
s++;
tr[x].ch[tmp]=s;
tr[s].ch[0]=0;
tr[s].ch[1]=0;
}
void add(int x)//在字典树上加值
{
int now=0;
for (int i=30;i>=0;i--)
{
int p;
if ((1<<i)&x) p=1;
else p=0;
if (!tr[now].ch[p]) newnode(now,p);
now=tr[now].ch[p];
}
}
int solve(int x)//贪心的找最优序列
{
int now=0,tmp=0;
for (int i=30;i>=0;i--)
{
int p;
if ((1<<i)&x) p=0;
else p=1;
if (tr[now].ch[p]) tmp+=(1<<i);
else p^=1;
now=tr[now].ch[p];
}
return tmp;
}
int main()
{
scanf("%d",&n);
tot=1,ans=0,s=0;
tr[s].ch[0]=0;
tr[s].ch[1]=0;
for (int i=1;i<=n-1;i++)
{
int ui,vi,wi;
scanf("%d%d%d",&ui,&vi,&wi);
ui-=1;
vi-=1;
addedge(ui,vi,wi);
}
dfs(0,0);
for (int i=0;i<n;i++)
{
ans=max(ans,solve(val[i]));
add(val[i]);
}
printf("%d\n",ans);
}
#include <cstdio>
#include <cstring>
#define maxn 100010
struct node{
node *son[2];
node(){son[0]=son[1]=NULL;}
};
node *root=new node();
int n;
struct edge{int y,z,next;};
edge e[maxn*2];
int first[maxn];
void buildroad(int x,int y,int z)
{
static int len=0;
e[++len]=(edge){y,z,first[x]};
first[x]=len;
}
int ans=0;
void check(int x)
{
node *now=root;int sum=0;
if(root->son[0]==NULL&&root->son[1]==NULL)return;
for(int i=30;i>=0;i--)
{
int p=1;
if((x&(1<<i))>0)p=0;
if(now->son[p]!=NULL)sum^=(1<<i),now=now->son[p];
else now=now->son[p^1];
}
if(sum>ans)ans=sum;
}
void add(int x)
{
node *now=root;
for(int i=30;i>=0;i--)
{
int p=0;
if((x&(1<<i))>0)p=1;
if(now->son[p]==NULL)now->son[p]=new node();
now=now->son[p];
}
}
void dfs(int x,int fa,int dis)
{
for(int i=first[x];i;i=e[i].next)
{
int y=e[i].y;
if(y==fa)continue;
check(dis^e[i].z);add(dis^e[i].z);
dfs(y,x,dis^e[i].z);
}
}
int main()
{
scanf("%d",&n);
for(int i=1,x,y,z;i<n;i++)
scanf("%d %d %d",&x,&y,&z),buildroad(x,y,z),buildroad(y,x,z);
dfs(1,0,0);
printf("%d",ans);
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号