栈与catalan数

组合数学Catalan数

http://www.cppblog.com/MiYu/archive/2010/08/07/122573.html  这个讲的很清楚（catalan数的应用）

(1)定义：

Cn=1/n+1 (2n n)----->组合计数，catalan数是很多组合计数应用问题的数学模型

模型1：Cn=1/(n+1)(2n n)=(2n n)-(2n n+1)=(2n n)-(2n n-1)----->把n个1和n个0排成一行，使这一行的任意前k个数中1的数量总是大于等于0的数量，这样的排列一共有多少个？---->Cn个

模型2：Cn=C0Cn-1+C1Cn-2+......+Cn-1C0,  C0=1

其实，许多看似不相关的问题都和Catalan数有密切关系。

1）n个节点构成的二叉树共有多少种情况---对应模型2。

2）栈的计数：一共n个数通过一个栈，能够产生多少个序列----对应模型1

3）棋盘问题：hdu2067  n行n列的棋盘，从左下角走到右上角，一直在对角线右下方走，不穿过主对角线，共有多少种走法---对应模型1

4）括号问题：用n个左括号和n个右括号组成的括号字符串一共有多少种组合？----对应模型2

5）买票找零问题，三角剖分问题

6）类似的利用Catalan数求解的问题有NOI2001福建组队赛《球迷购票问题》等，类似的递推问题还有NOI2000福建组队赛《车皮排序问题》等

（2）计算

1）Cn=C0Cn-1+C1Cn-2+......+Cn-1C0,  C0=1     --->n<=100，一般用于需要输出catalan数的数值  int64

2）Cn=4n-2/n+1 Cn-1  C0=1     --->可以看出以4n的倍数增长

3）Cn=1/n+1 (2n n)=（2n)!/(n+1)/!n!

用公式2、3一般是需要进行取模，都有大整数除法，所以需要转换为逆元，然后再取模

NOIP 2003 普及组试题《栈的计数》

这道题的递归解法，以及推出来的Catalan解法

https://blog.csdn.net/ivy_uu/article/details/72835696

这个的解决方法其实就是这个规律

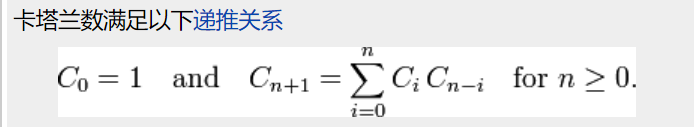
#include<cstdio>
#define maxn 20
using namespace std;
int n,f[maxn];

int main()
{
  int i,j,k;
  scanf("%d",&n);

  f[0]=f[1]=1;
  for(i=2;i<=n;i++)
    for(j=0;j<=i-1;j++)
      f[i]+=f[j]*f[i-j-1];
  printf("%d\n",f[n]);    
  return 0;
}

介绍了三种算法

算法一：（分治） 
我们不妨直接设n辆火车产生的排列总数为f(n)。看看能不能找到一些规律。 
如图,n列火车通过栈,起始车头在车列最前端。经过移动后,车头处在了第a+1位,车头前有a辆车,车头后有b辆车(a>=0,b>=0)。则n=a+b+1,b=n-a-1。

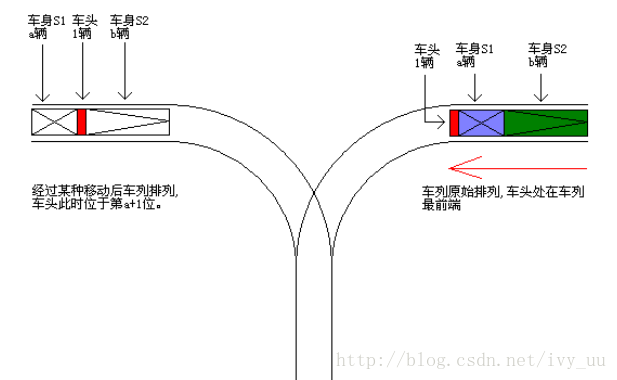
若要达到上述移动目的,步骤为:
(1)将车头进栈;
(2)将车头后a辆车依次通过栈，移至轨道另一端；
(3)将车头出栈，则车头恰好排在第a+1位；
(4)将轨道右端剩余b辆车依次通过栈，移至轨道另一端；
不难证明，移动方案仅此一种。问题是每个步骤又有许多种不同的移动方法。显然步骤
（1）（3）各只有一种移动方法。仔细观察步骤（2）（4）。我们前面定义了“n辆火
车依次通过栈产生的排列总数为f(n)”，而步骤（2）恰恰是这个问题的子问题。即步骤
二可写为“将a辆火车依次通过栈”，根据前面定义，其移动方案总数为f(a)。同理，步
骤(4)的移动方法总数为f(b)。

根据乘法原理，要完成上述工作：
总的方法数tot=步骤(1)的方法数步骤(2)的方法数步骤(3)的方法数*步骤(4)的方法数
=1* f(a) * 1* f(b)
=f(a) * f(b)
=f(a) * f(n-a-1) (因为b=n-a-1)

我们目前已求得将n列火车通过栈，且将位于原车列首位的车头经过移动后位于移动后的
车列第a+1位的方法总数, 即f(a)*f(n-a-1)。但是原火车头经过移动后可能处在移动后车
列的任意一个位置，即a的取值是任意的。由于共有n辆车，因此移动后原火车头前面的
车数可能有0~n-1辆，即0≤a≤n-1。

要完成某个特定的移动方法，a只能取某个特定的值。根据加法原理，将n辆火车依次通
过栈的移动总数为：
总的方法数 f(n) = 取a=0的方法数 + 取a=1的方法数 + … + 取a=n-1的方法数  ！！！！！！！是累加
= f(0)*f(n-0-1) + f(1)*f(n-1-1) + f(2)*f(n-2-1) + … + f(n-1)*f(n-(n-1)-1)
即f(n)= (n≥1)
边界值：f(0)=1;
有了以上递归公式，不难用递推的方法写出程序。

算法二(dp或者dfs)：

前面所说的搜索法虽行不通，但它也许能给我们一些提示。如果用深度优先搜索(DFS)，穷举所有可能的移动方法来做的话，当搜索到某个状态下，所能做的移动方法无非有两种：（1）将轨道右方的第一列火车进栈；（2）将栈顶的火车出栈，进入左边的轨道。
设此时轨道右方，栈，轨道左方的火车数分别为a,b,c。我们就能用(a,b,c)表示出当前的状态。显然n=a+b+c,则c=n-a-b。即已知a和b，c就被确定，所以我们可以用(a,b)来作为状态的表示方法。则起始状态为(n,0)，目标状态为(0,0)。又由上面的两种移动方法。我们可类似的得到两种状态转移方式：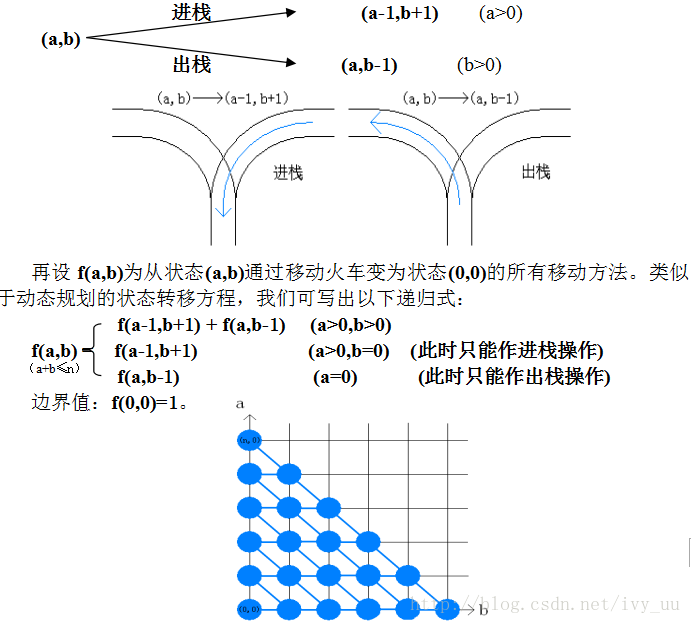

按a的值从0~n划分阶段，亦可通过递推求得f(n,0)的值，即为所求。如果只保存两个阶段进行递推，还可将空间复杂度降为O(n)。这个算法虽然不如算法一简洁，但对于本题来说已经很不错了。而且它在思维难度上要比算法一容易一些。

 

算法三：
对于算法一中的数列f(i)来说，每一项都是被唯一确定的。那么我们是否可以找到其通项
公式，从而直接算出f(i)呢？
答案是肯定的。本题实际是一个经典的Catalan数模型。有关Catalan数的详细解释请参
考《组合数学》等书。对于数列f(i)有公式可直接算出：

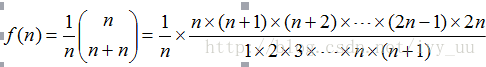
具体实现时，若直接用上述公式计算，对数字的精度要求较高。可将其化为递归式:

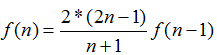
再进行递推计算，并且注意类型的定义要用comp型。
其实，许多看似不相关的问题都和Catalan数有密切关系。例如所有节点数为n的二叉树的个数就恰为上式中的f(n)。因此，Catalan数的应用范围很广。

 

我总结了一下，最典型的四类应用：（实质上却都一样，无非是递归等式的应用，就看你能不能分解问题写出递归式了）
1.括号化问题。

　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)
2.出栈次序问题。

　　一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
　　类似：
　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。

　　将一个凸多边形区域分成三角形区域的方法数?
　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
4.给顶节点组成二叉树的问题。
　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树!
　　先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +  + h(n-1)h(0)=h(n))
　　（能构成h（N）个）