二分的基本用途是在单调序列或单调函数中做查找操作
三分解决单调函数极值及相关问题,例如凸性函数,二次函数就是,利用函数的单峰性,如果函数不严格单调,那就不能适用
一本通题目
一、取余运算:输入b<span id="MathJax-Span-2" class="mrow"><span id="MathJax-Span-3" class="mi">,p,k 的值,求b^pmodk 的值。其中b、p、k长整型数。
就是快速幂
int modd(int x){ //代入的是次数
if(x==0) return 1; //这个一定的要
int tmp=modd(x/2)%k; //注意逻辑关系
tmp=tmp*tmp%k;
if(x%2==1) tmp=(tmp*b)%k;
return tmp;
}
快速幂的迭代写法
LL ans=1;
LL a,b,m;
while(b>0){
if(b&1){
ans=ans*a%m;
}
a=a*a%m;
b>>=1;
}
二、网线主管
给定N,K,为绳子的个数和需要的数量,然后在给定N个绳子的长度,求能够切割成K个,且切割后长度最大的长度为多少,这道题其实没有想象的复杂,分治就好了
,但是要注意对 细节的处理,double、int类型的处理
double a[10001];
int b[10001],n,m,l,r;
bool judge(int x){
int ans=0;
for(int i=1;i<=n;i++) ans+=b[i]/x; //都是转换为了整数进行运算
return ans>=m;
}
int main(){
cin>>n>>m;
l=r=0;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=(int)(a[i]*100+0.5); //写法!!!(int)(x+0.5)
if(b[i]>r) r=b[i];
}
r+=1; //用分治来选择,这里r+1!!!!
while(l+1<r){
int mid=(l+r)/2;
if(judge(mid)) l=mid;
else r=mid;
}
printf("%.2lf\n",l/100.0);
三、月度开销
int a[100001],n,m,sum=0;
int l,r ;
bool judge(int x){
int c=0,b=0,i;
for(i=1;i<=n;i++){
b+=a[i];
if(b>=x){
c++;
if(a[i]<x) b=a[i];
else return 1;//a[i]>=x左边界left=mid;嗯。。不太懂 ------其实是如果一个单个的天开销都比划定的月度开销大,那么肯定阅读开销应该更大才对
//所以返回1,然l改为mid,把月度开销调大(666)
}
}
return c>=m;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
sum+=a[i];
}
l=1;
r=sum; //注意这里的r选择,,,是选的月度开销
while(l+1<r){
int mid=(l+r)/2;
if(judge(mid)) l=mid;
else r=mid;
}
if(judge(l)) cout<<l<<endl;
else cout<<r<<endl;
return 0;
}
四、和为给定数,简单,two pointers
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int left=1,right=n;
cin>>m;
sort(a+1,a+n+1);
while(left<right){
if(a[left]+a[right]==m){
cout<<a[left]<<" "<<a[right]<<endl;//找到了就退出,这个其实就是two pointers的思想
break;
}
else if(a[left]+a[right]>m) right--;
else left++;
}
if(left==right) cout<<"No"<<endl;
return 0;
}
五、河中跳房子
cin>>s>>n>>m;
for(int i=1;i<=n;i++) cin>>dis[i];
dis[0]=0;
dis[n+1]=s;
int i=0,j,ans=0;
l=0;r=s+1;//左边右边赋值 //枚举的是距离!!只要超过这个距离就移除
while(l+1<r){
int mid=(l+r)/2;
ans=0;
i=0;
while(i<=n){
j=i+1;
while(j<=n+1&&dis[j]-dis[i]<mid) j++; //主义者里面的写法
ans+=j-i-1;//注意还要减一
i=j;//这里不能减了就移动i;
}
//上面这个while是用来计算这次的Mid能够移去多少块石头
if(ans<=m) l=mid; //如果少了,就说明mid太小了,不行就只能把left置为mid,让mid变大
else r=mid;
}
cout<<l<<endl;
六、2012,给定一个最多为200位的数N,求2012^N的最后四位
char a[N];
int main()
{
int k;
cin>>k;
while(k--)
{
cin>>a;
int len=strlen(a);
int B=0,C=2011;
int i;
for(i=len-4;i<len;i++)
if(i>=0)
B=B*10+a[i]-'0';
i=1;
do{
if(i*2<=B)
{
i*=2;
C=(C*C)%10000;
}
}while(i*2<=B);
for(;i<B;i++)
C=(C*2011)%10000;
cout<<C<<endl;
}
return 0;
}
一本通提高篇
1433:【例题1】愤怒的牛
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//排序之后,通过二分距离,找到距离最接近放下
int n,c;
int a[maxn];
bool check(int d){
int cow=1;
int now=a[1]+d;
for(int i=2;i<=n;i++){
if(a[i]<now) continue;
cow++;
now=a[i]+d;
}
return cow>=c;
}
int main(){
scanf("%d %d",&n,&c);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
int l=0,r=a[n]-a[1]; //!!!二分
while(l<=r){
int mid=(l+r)/2;
if(check(mid)) l=mid+1;
else r=mid-1;
}
printf("%d\n",r);
return 0;
}
1434:【例题2】Best Cow Fences
让序列每个值减去平均值(模拟的mid),判断这个长度不小于L的子序列和是否大于还是小于0,注意!! r-l>eps eps=1e-5
初始值也是 l=1e-6,r=1e6
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn= 100010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//1.是否存在一个长度不小于L的子段,子段序列和为非负。及二分查找
//2.子段序列和可以是后段减前段
double a[maxn],b[maxn],summ[maxn];
const double ex=1e-5;
int n,L;
int main(){
scanf("%d %d",&n,&L);
for(int i=1;i<=n;i++){
scanf("%lf",&a[i]);
}
double l=1e-6,r=1e6,mid;
while(r-l>ex){
mid=(l+r)/2;
for(int i=1;i<=n;i++) b[i]=a[i]-mid;
for(int i=1;i<=n;i++) summ[i]=(summ[i-1]+b[i]);
double ans=-INF;
double minn=INF;
for(int i=L;i<=n;i++){
minn=min(minn,summ[i-L]);
ans=max(ans,summ[i]-minn); //前缀和相减
}
if(ans>=0) l=mid;
else r=mid;
}
printf("%d\n",int(r*1000));
return 0;
}
1435:【例题3】曲线
二次函数求极值:三分
eps搞得很小,反正管的他的
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn= 1e5+100;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int t,n;
//三分,因为形成的是凸函数
double a[maxn],b[maxn],c[maxn];
double eps=1e-9;
double js(double x){
double maxx=-INF;
for(int i=0;i<n;i++){
maxx=max(maxx,a[i]*x*x+b[i]*x+c[i]);
}
return maxx;
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%lf %lf %lf",&a[i],&b[i],&c[i]);
}
double l=0,r=1000,lm,rm;
while(fabs(r-l)>eps){
lm=l+(r-l)/3.0;
rm=r-(r-l)/3.0;
if(js(lm)>js(rm)) l=lm;
else r=rm;
}
printf("%.4lf\n",js(r));
}
return 0;
}
1436:数列分段II
对于给定的一个长度为N的正整数数列A[i],现要将其分成M(M≤N)段,并要求每段连续,且每段和的最大值最小。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=100001;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int n,m;
int a[maxn];
/*
二分答案
我们最终答案的取值区间是[ max(a[i]) , ∑a[i] ]
设定 l=max(a[i]) , r=∑a[i] , mid不断二分
mid表示每段和的最大值,也就是每段和都不超过mid
放到check函数里,计算一下在mid为最大值的情况下可以分成多少段
如果段数 cnt > m ,说明这个mid小了,它还可以再大一点
如果段数 cnt <= m , 说明这个mid大了,那么它就要小一点了,由于此时cnt可能等于m,这个mid为候选答案,记录下来(如果他是真正答案,最后输出的就是他,否则他会被更新为一个更小的)
*/
int check(int x){
int ans=1;
int tmp=a[1];
for(int i=2;i<=n;i++){
if(tmp+a[i]<=x){
tmp+=a[i];
}
else{
ans++;
tmp=a[i];
}
}
return ans<=m;
}
int main(){
scanf("%d %d",&n,&m);
int l=-INF,r=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
l=max(l,a[i]);
r+=a[i];
}
int mid,ans;
while(l<=r){
mid=(l+r)/2;
//cout<<l<<" "<<r<<endl;
if(check(mid)){
ans=mid;
r=mid-1;
}
else l=mid+1;
}
printf("%d",ans);
return 0;
}
1437:扩散
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=52;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//没见过世面TATTAT。。。。。
//数学知识
/*
两个点a、b连通,记作e(a,b),当且仅当a、b的扩散区域有公共部分。
连通块的定义是块内的任意两个点u、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。
也就是说一个点扩散到另一个点的 时间 就是他们的横纵坐标差值的和(xi-xj)+ ( yi-yi )
如果 时间<mid2 就说明两个块连通(注意mid要2,因为两个点同时扩散)
然后用并查集储存连通块
*/
//https://blog.csdn.net/justidle/article/details/104355432
struct node{
int x,y;
}nodes[maxn];
int dis[maxn][maxn]; //曼哈顿距离
int spread[maxn]; //上一次的扩散位置
bool check(int x,int n){
//根据扩散时间x,遍历所有点,查找是否存在连通
bool vis[maxn]={};
int step=0;
int tim=1; //看在这前有没有交集
spread[1]=1;
vis[1]=1;
while(step!=tim){
step++;
for(int i=1;i<=n;i++){
if(vis[i]) continue; //已经访问,则跳过
//每次取中间点 mid 后,从任意一个点出发尝试遍历所有点。a 能达到 b 的条件一定是 a 到 b 的曼哈顿距离不超过 2 倍的 mid 值。如果能成功遍历所有点,说明当前 mid 符合条件;反之,则不符合条件。
if(dis[spread[step]][i]<=2*x) {
vis[i]=1;
spread[++tim]=i;
}
}
}
return tim==n;
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d %d",&nodes[i].x,&nodes[i].y) ;
}
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
dis[i][j]=dis[j][i]=abs(nodes[i].x-nodes[j].x)+abs(nodes[i].y-nodes[j].y);
}
}
int l=0,r=1e9,mid;
//符合条件,右边界移动,我们尝试更小 mid 的可能性。如果不符合条件,左边界移动,我们尝试更大 mid 的可能性。
//直到不符合二分查找条件,即 left ≤ right,不成立。right 就是我们需要的答案。
while(l<=r){
mid=(l+r)/2;
if(check(mid,n)) r=mid-1;
else l=mid+1;
}
printf("%d\n",l);
return 0;
}
1438:灯泡
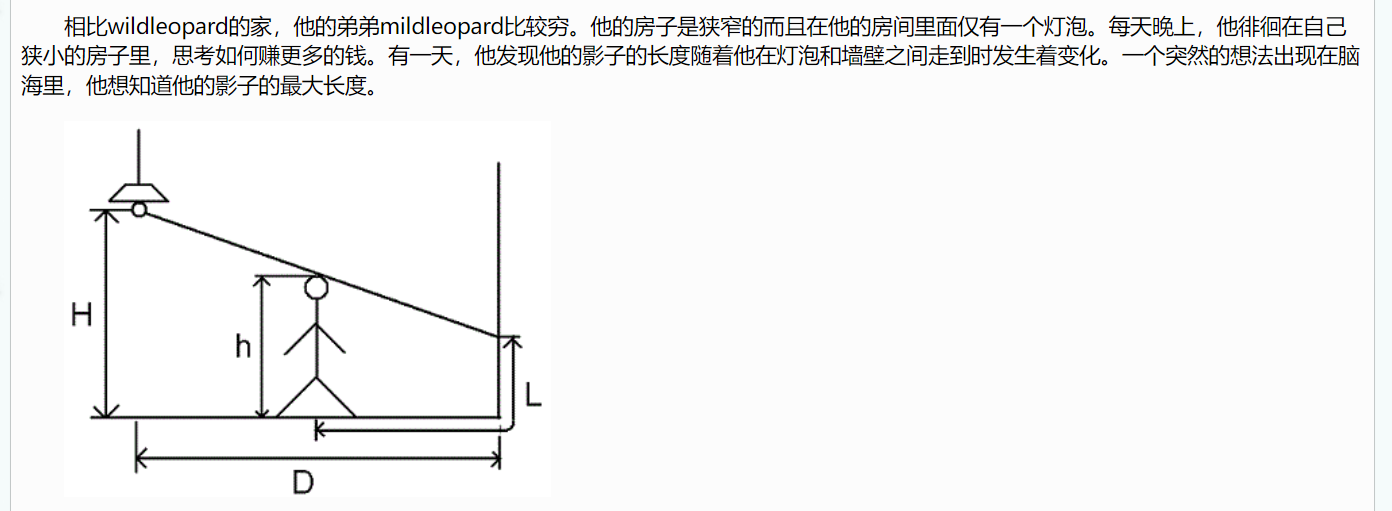
这道题都可以算是数学题了,主要用等比三角形算出表达式,然后根据式子单调用三分
(37条消息) 一本通题解——1438:灯泡_努力的老周的博客-CSDN博客
#include <bits/stdc++.h>
using namespace std;
double H, h, D;//由于check函数需要用的,就用全局变量吧
double check(double x) {
if ((H-h)/x*(D-x)>h) {
//灯的高度小于影子到墙底部距离。属于第二种情况
return x/(H-h)*h;
} else {
//属于第一种情况
return D-x+h-(H-h)/x*(D-x);
}
}
int main() {
int t;
cin>>t;
int i, j;
for (i=0; i<t; i++) {
cin >> H >> h >> D;
//三分查找
double eps = 1e-8;
double left=0;
double right=D;
double l_mid, r_mid;
while (left+eps<right) {
l_mid = left+(right-left)/3;
r_mid = right-(right-left)/3;
if (check(l_mid) > check(r_mid)) {
right = r_mid;
} else {
left = l_mid;
}
}
printf("%.3lf\n", check(left));
}
return 0;
}
1439:【SCOI2010】传送带

这个是两层三分
首先要假装确定E点位置,然后三分F点,然后再三分E点的时候就可以真的确定E点
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-8; //我一般喜欢把eps设为1e-8,当然对于这题1e-6足够了
double ax,ay,bx,by,cx,cy,dx,dy,p,q,r;
double dis(double x_1,double y_1,double x_2,double y_2){ //P1和P2的距离
double xdis=x_1-x_2,ydis=y_1-y_2;
return sqrt(xdis*xdis+ydis*ydis);
}
double f(double x_1,double y_1,double x_2,double y_2){ //上文中提到的f(P1)在当F是P2时的值
return dis(x_1,y_1,x_2,y_2)/r+dis(x_2,y_2,dx,dy)/q;
//第一个是dis(E,F)/r,第二个是dis(F,D)/q
}
double calc1(double x,double y){ //内层三分F(这个给定的参数是固定E是这个点)
double lx=cx,ly=cy,rx=dx,ry=dy; //在CD上三分
while(dis(lx,ly,rx,ry)>eps){ //还没有重合成一点
double tmpx=(rx-lx)/3,tmpy=(ry-ly)/3;
double lmidx=lx+tmpx,rmidx=rx-tmpx,lmidy=ly+tmpy,rmidy=ry-tmpy; //(lmidx,lmidy)是左等分点,(rmidx,rmidy)是右等分点
double ans1=f(x,y,lmidx,lmidy),ans2=f(x,y,rmidx,rmidy); //左等分点和右等分点的值
if(ans2-ans1>eps) rx=rmidx,ry=rmidy; //左边更小,舍弃右边
else lx=lmidx,ly=lmidy; //右边更小,舍弃左边
}
return f(x,y,lx,ly); //返回这个最小值
}
double calc(){ //外层三分E
double lx=ax,ly=ay,rx=bx,ry=by; //在AB上三分
while(dis(lx,ly,rx,ry)>eps){
double tmpx=(rx-lx)/3,tmpy=(ry-ly)/3;
double lmidx=lx+tmpx,rmidx=rx-tmpx,lmidy=ly+tmpy,rmidy=ry-tmpy; //以上同理
double ans1=calc1(lmidx,lmidy)+dis(ax,ay,lmidx,lmidy)/p,ans2=calc1(rmidx,rmidy)+dis(ax,ay,rmidx,rmidy)/p; //左等分点和右等分点的值(在这里套了内层三分)
if(ans2-ans1>eps) rx=rmidx,ry=rmidy;
else lx=lmidx,ly=lmidy; //同理
}
return calc1(lx,ly)+dis(ax,ay,lx,ly)/p; //返回最小值,也就是答案
}
int main(){
scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf",&ax,&ay,&bx,&by,&cx,&cy,&dx,&dy,&p,&q,&r);
printf("%.2lf\n",calc()); //这就是答案
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号