递归题目

一本通

递归太常用了，其实很多时候在复杂的代码里面理解起来还比较麻烦

在排序里面的应用：快速排序和归并排序

经典例题：汉诺塔

#include<bits/stdc++.h>
using namespace std;
int n,k;
void mov(int n,char a,char c,char b){ //借助b，将a上的n片移到c上 
	if(n==0) return;
	mov(n-1,a,b,c);
	k++;
	cout<<k<<":from  "<<a<<"-->"<<c<<endl;
	mov(n-1,b,c,a);
} 
int main()
{
    cout<<"n=";
    cin>>n;
    mov(n,'a','c','b');
    return 0;
}
 

　　

一、数的计数

//方法1 递归 
int dfs1(int n){
	int i;
	ans++;
	for(i=1;i<=n/2;i++) dfs1(i);//很简单但很强大！！注意逻辑 但是超时！ 
}
//方法2：记忆化搜索
int h[1001];
void dfs2(int n){
	if(h[n]!=-1) return ;
	h[n]=1;
	for(int i=1;i<=n/2;i++) {
		dfs2(i);
		h[n]+=h[i];
	} 
} 
//方法3：递推
int dfs3(int n){
	for(int i=1;i<=n;i++){
		h[i]=1;
		for(int j=1;j<=n/2;j++) h[i]+=h[j];
	}
	return h[n];
} 
//方法4：定义数组，将时间复杂度降低到O(n)
int s[1001];
void dfs4(int n){
	for(int i=1;i<=n;i++){
		h[i]=1+s[i/2];
		s[i]=s[i-1]+h[i];
	}
	cout<<h[n]<<endl;
}

1315：【例4.5】集合的划分

这个和分苹果不一样，不能有空的

但是注意是苹果是不一样的

#include<bits/stdc++.h>
using namespace std;
int s(int n,int k){
	if((n<k)||(k==0)) return 0;
	if((k==1)||(k==n)) return 1;
	return s(n-1,k-1)+k*s(n-1,k);
}
int main()
{
    int n,k;
    cin>>n>>k;
    cout<<s(n,k);
    return 0;
}
 

　　在这也放一下放苹果

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int get(int m,int n){
	if(m==0||n==1) return 1;
	if(m<n) return get(m,m);
	else return get(m,n-1)+get(m-n,n);
} 


int main(){
int sum;
int m,n;
cin>>sum;
while(sum--){
	cin>>m>>n;
	cout<<get(m,n)<<endl;
}

return 0;
}

　　

二、逆波兰表达式

逆波兰表达式是一种把运算符前置的算术表达式，例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系，也不必用括号改变运算次序，例如(2 + 3) * 4的逆波兰表示法为* + 2 3 4。本题求解逆波兰表达式的值，其中运算符包括+ - * /四个。

#include <stdio.h>
#include<stdlib.h>
double exp()
{
    char s[210];
    scanf("%s", s);
    switch(s[0])
    {
        case'+': return exp( ) + exp( );
        case'-': return exp( ) - exp( );
        case'*': return exp( ) * exp( );
        case'/': return exp( ) / exp( );
        default: return atof(s);
    }
}
int  main()
{
    double ans;
    ans = exp();
    printf("%lf", ans);
    return 0;
}

三、全排列

其实就算是深搜和回溯

void fs(int x){
	for(int i=0;i<len;i++){
		if(c[i]==0) {
			b[x]=i;
			c[i]=1;
			fs(x+1); //这里就算递归
			c[i]=0; //回溯一步 
		}
	}
	if(x==len-1){
	for(int i=0;i<len;i++) cout<<a[b[i]];
	cout<<endl; 
} 
}

四、分解因数

求一个数n被分解后有多少种情况

 

 

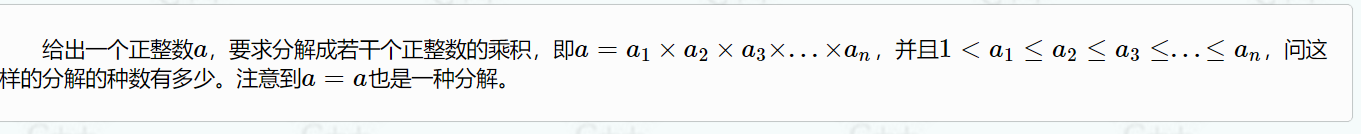
//方法1 
void js(int x,int y){
	if(x==1) ans++;
	for(int i=y;i<=x;i++){
		if(x%i==0) js(x/i,i);  //这里通过控制i的下限来避免的重复计算！！！注意技巧! 
	}
}
//方法2
int change(int n,int m){
	if(n==1) return 1;
	else if(n==0||m==1) return 0;
	else if(m>n) return change(n,n);
	else if(n%m==0) return change(n/m,m)+change(n,m-1); //分除与不除的情况
	else return change(n,m-1);
} 

五、括号匹配，有输出不对的情况下的字符串

stack<int> p;
//用来存储下标，不是char！！！ 
char a[101],b[101];
int len;
int main(){
	while(cin>>a){
		len=strlen(a);
		for(int i=0;i<len;i++){
			if(a[i]=='('){
				p.push(i); //存入下标
				b[i]=' ';  //先做空格处理，后面不能抵消的再换为错误标志 
			}
			else if(a[i]==')'){
				if(!p.empty()){
					p.pop();
					b[i]=' ';
				}
				else b[i]='?';
			
			}
			else b[i]=' ';
		}
		while(!p.empty()){
			b[p.top()]='$';
			p.pop();
		}
		
		b[len]='\0';
		//这句话！导致没有通过 
		cout<<a<<endl;
		cout<<b<<endl;
	}
return 0;
}

六、2的幂次方表示

137可表示为：

2(2(2)+2+2(0))+2(2+2(0))+2(0)

int get(int x){
	if(x==0){
		cout<<"0";
		return 0;
	}
	if(x==2){
		cout<<"2";
		return 0;
}
	while(1){
	int i;
	for(i=17;a[i]>x;i--) ;//寻找小于x的第一个下标i
	if(a[i]!=2) {
		cout<<"2(";
		get(i); //这里递归 
		cout<<")";
	}
	else cout<<"2";
	if(x-a[i]) {              //箭头向上！！还有剩的！！ 
		cout<<"+";
		x=x-a[i];//上面的处理完了后进行这一步,因为有while 
	}
	else return 0;
}
}
//这个为另外一种做法：递归 
void calculate(int n,int step)
{
    if(n==0)
        return;
    calculate(n/2,step+1);
    if(n%2)
    {
        if(n/2)
            cout<<"+";
        if(step==1)
            cout<<"2";
        else
        {
            cout<<"2(";
            if(step==0)
                cout<<"0";
            else
                calculate(step,0);
            cout<<")";
        }
    }
}

七、判断元素是否存在

bool get(int x){
	if(x>b) return 0; //注意这个条件直接判断 
	if(x==b) return 1;
	if(x<b) return get(2*x+1)||get(3*x+1); //从底层开始算 
}

　　

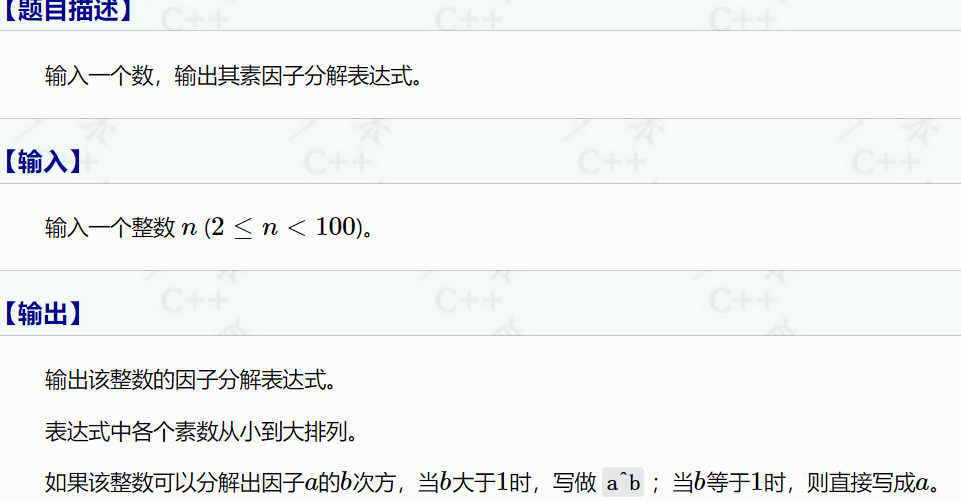
1210：因子分解

 

 

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
using namespace std;
int a[101];
int get(int x,int y){
	if(x==0||y>x) return 0;
	while(x%y==0){
		x/=y;
		a[y]++; //次数开始加 
	}
	get(x,y+1); //这里不用专门去算素数，因为不是素数的已经被除掉了 
}


int main(){
	int n;
	cin>>n;
	get(n,2); //从2开始计算
	bool ok=0;//标记是否是第一次除，因为不能多输出符号
	for(int i=2;i<=n;i++){
		if(ok&&a[i]) cout<<"*";
		if(a[i]) ok=1;//标记因为已经遇到第一个
		if(a[i]==1) cout<<i;
		else if(a[i]>1) cout<<i<<"^"<<a[i]; 
	} 
return 0;
}