一本通的题
一、昆虫繁殖
#include<iostream>
using namespace std;
//昆虫繁殖
int main(){
long long a[101]={0},b[101]={0},i,j,x,y,z;
cin>>x>>y>>z;
for(i=1;i<=x;i++) {a[i]=1;b[i]=0; //成虫和幼虫
}
for(i=x+1;i<=z+1;i++){ //注意下标,从x+1开始到第z+1个月
b[i]=y*a[i-x];//b[i]表示这个月的幼虫
a[i]=a[i-1]+b[i-2]; //表示成虫
}
cout<<a[z+1]<<endl;
return 0;
}
二、位数问题
n位数中,有偶数个3的个数
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
int n,a[1001][2];
//这道题的思想,用递推,从上一位数的结果退出这一位的结果
//
int f=9;
int main(){
cin>>n;
a[1][0]=9;//0也是偶数!!
a[1][1]=1;
for(int i=2;i<=n;i++){
if(i==n) f=8; //最后一位的取值再1-2, 4-9之间
a[i][0]=(a[i-1][0]*f+a[i-1][1])%12345; //注意f的位置 //偶数个
a[i][1]=(a[i-1][1]*f+a[i-1][0])%12345; //奇数个
}
cout<<a[n][0]<<endl;
return 0;
}
三、经典的放苹果问题
把n个同样的苹果放在m个同样的盘子里,允许有的盘子空着不放,有多少种方法?-------分为有无空盘
(1)边界条件:n=0或者m=1 一种方法
(2)没有空盘,那么先给每个盘子分配一个,所以有a[n-m][m]种,有一个空盘,有a[n][m-1]种
(3)ps.如果n<m 那个结果为a[n][n]
for(int n=0;n<=10;n++){//苹果
for(int m=0;m<=10;m++){//盘子
if(n==0||m==1) a[n][m]=1; //只有一个盘子或者0个苹果都是一种情况
else if(n>=m) a[n][m]=a[n][m-1]+a[n-m][m]; //分为有无空盘
else a[n][m]=a[n][n];
}
}
数的划分(其实就是n=m的放苹果问题)
可以递推,也可以动态规划,是十分经典的题
1、递推
用f[n][m]表示在值为n的情况,最大划分为m的值(每个盘子都放一个),根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2) 当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,…,1};
(3) 当n=m时,根据划分中是否包含n,可以分为两种情况:
(a). 划分中包含n的情况,只有一个即{n};
(b). 划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。 因此 f(n,n) =1 + f(n,n-1);
(4) 当n< m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5) 但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a). 划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,因此这种情况下为f(n-m,m)
(b). 划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);因此 f(n, m) = f(n-m, m)+f(n,m-1);
综上所述:
f(n,m)=1; (n=1 or m=1)
f(n,m)=f(n, n); (n<m)
f(n,m)=1+ f(n, m-1); (n=m)
f(n,m)=f(n-m,m)+f(n,m-1); (n>m)
二、动态规划
状态转移方程:
当 n == 1 || k == 1 时,f(n, k) == 1, n为1,那么只能为1; 而k为1,那么只能划分成n个1.
当 n < k 时,f(n, k) == f(n, n),因为n的划分中不可能出现比n大的数,所以可以将最大值从k降到n;
当 n >= k 时,f(n, k) = f(n-k, k) + f(n, k-1), 前半部分是划分中存在最大值k,所以可以在(n-k)中继续以最大值为k来划分,而后半部分则是划分中最大值不是k,那么其结果和以(k-1)为最大值的划分是一样的。在初始化中可以将f(0, k)初始化为1,及对应f(n, n)可能出现的情况。
综合来说,使用递归更加容易理解,不过使用动态规划时间消耗更小。
#include<iostream>
using namespace std;
long long d[125][125];
void dp()
{
for(int i=1;i<=120;i++)
d[i][1]=d[1][i]=d[0][i]=1;
for(int i=2;i<=120;i++)
for(int j=2;j<=120;j++)
{
if(i<j)
d[i][j]=d[i][i];
else
d[i][j]=d[i-j][j]+d[i][j-1];
}
}
int main()
{
int n;
dp();
while(cin>>n)
cout<<d[n][n]<<endl;
return 0;
}
四、 判断整除
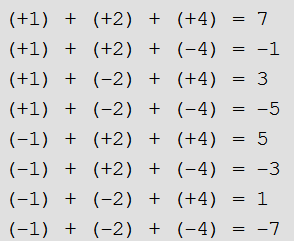
将前n-1个数看成一个整体序列,则n个数可能产生的结果就等于“前n-1个数产生的所有结果分别加上第n个数或分别减去第n个数”
n-2也同理……直到1为止。
由于是判断有无结果能被k整除,所以所有的中间结果都可以取余k,从而使所有可能的结果保持在一个不大的范围,用数组进行存储。
下面代码中的ans[i][j]表示i个数的序列有没有取余k后为j的结果,0表示没有,1表示有。
这道题不如过说是逻辑和取余运算的例题了。。。。
//判断整除
//哎
int a[10001][101]; //记录计算结果和过程的
int n,k;
int b[10001];//记录数组的
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>b[i];
b[i]%=k; //这一步!!!
}
//初始化
memset(a,0,sizeof(a));
a[1][b[1]]=1;
a[1][-b[1]+k]=1;
for(int i=1;i<n;i++){ //小于n,因为最后会算到n
for(int j=0;j<k;j++){
if(a[i][j]){
a[i+1][(j+b[i+1])%k]=1; //注意这里都是a[i+1] 还有 b[i+1]
a[i+1][(j+(-b[i+1]+k))%k]=1;
}
}
}
if(a[n][0]==1) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
五、山区建小学
cin>>n>>m;
memset(a,0,sizeof(a));
for(int i=1;i<n;i++){ //注意次数是输入n-1个数
cin>>dis[i][i+1];
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
dis[i][j]=dis[j-1][j]+dis[i][j-1]; //
dis[j][i]=dis[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
int mid=(i+j)/2;
a[i][j]=0;
for(int k=i;k<=j;k++) a[i][j]+=dis[k][mid]; //在两地间建小学最近,然后用a[i][j]存储在i和j中间建小学的最短距离
}
}
for(int i=1;i<=n;i++) dp[i][1]=a[1][i];
//注意理解这段话的意思,前i个村庄建1个学校和在1和村庄i中间建一个是等价的
for(int i=1;i<=n;i++){
for(int j=2;j<=m;j++){ //注意j从多少开始
dp[i][j]=0xf7fffffff;
for(int k=j-1;k<=i;k++){ //a[][]数组其实用了贪心的思想
//再前k个村庄里面建j-1个学校,再k+1--i之间再建一所学校,建在“中间”
dp[i][j]=min(dp[i][j],dp[k][j-1]+a[k+1][i]); //k在枚举i与j之间的村庄
}
}
}
cout<<dp[n][m]<<endl;
六、流感传染,这道题需要用两个数组,保存,一个保存今天的,昨天的,因为今天被感染的只能从明天开始感染别人
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) {
cin>>a[i][j];
aa[i][j]=a[i][j];
}
int m;cin>>m;
for(int day=1;day<=m;day++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
if(a[i][j]=='@') bf(i,j);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) a[i][j]=aa[i][j]; //注意这里的赋值顺寻
P2696 慈善的约瑟夫
实在是看不懂递推。。。用模拟做的
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
//新约瑟夫问题,真的看不懂递推,只懂模拟、、、
int a[100005];
int num,f,n,s,x;
int main(){
cin>>n;
while(1){ //一直算到最后的胜利者就是编号最大的
num=n;
x=f=0;
memset(a,0,sizeof(a)); //表示有没有出队
while(num!=1){
x++;
if(x>n) x-=n;
if(a[x]!=0) continue;
f++;
if(f==2){ //交替出队
f=0;
a[x]=1;//出队了
num--;
}
}
for(int i=1;i<=n;i++){
if(a[i]==0){
if(i==n){
cout<<s+2*i<<endl;
return 0;
}
//如果不是的话,就处理这一轮的结果,把编号大于胜利者的 都踢出去
s=s+n-i; //出队的给一块
n=i; //剩下的人就只剩i个
break;
}
}
}
return 0;
}
【典型的递推关系】
1、Fibonacci数列
2、汉诺塔问题: hn=2*h(n-1)+1
3、平面分割问题:设有n条封闭曲线画在平面上,任何两条封闭曲线恰好交于两点,且任何三条封闭曲线不相交于同一点,问把平面分隔成多少个
h(n)-h(n-1)=2*(n-1)
4、catalan数:凸多边形的对角三角形剖分的个数 :组合数学
5、第二类stirling数:n个有区别的球放到m个没区别的盒子里,求放法
考虑第n个球:单独放一个盒子:S(n-1,m-1)
与别的球共占一个盒子:m*S(n-1,m)
所以方法是S(n,m)=S(n-1,m-1)+m*S(n-1,m) n>1,m>=1 边界条件为S(n,0)=0 S(n,1)=1 S(n,n)=1 S(n,k) =0(k>n)


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号