[斯坦福大学2014机器学习教程笔记]第五章-矢量
在这节中,我们将学习有关向量化的内容。无论你是用Ocatve,还是别的语言,比如MATLAB或者你正在用Python、NumPy 或Java、C、C++,所有这些语言都具有内置的,容易阅读和获取的各种线性代数库,它们通常写得很好,已经经过高度优化,通常是数值计算方面的博士或者专业人士开发的。而当你实现机器学习算法时,如果你能好好利用这些线性代数库,或者数值线性代数库,并联合调用它们,而不是自己去做那些函数库可以做的事情。如果是这样的话,那么通常你会发现:首先,这样更有效,也就是说运行速度更快,并且更好地利用你的计算机里可能有的一些并行硬件系统等等;其次,这也意味着你可以用更少的代码来实现你需要的功能。因此,实现的方式更简单,出错的可能性也就越小。举个具体的例子:与其自己写代码做矩阵乘法。如果你只在Octave中输入a乘以b,它会利用一个非常有效的做法,计算两个矩阵相乘。有很多例子可以说明,如果你用合适的向量化方法来实现,你的代码就会简单得多,也有效得多。
让我们来看一些例子:这是一个常见的线性回归假设函数:hθ(x) = Σθjxj。如果你想要计算hθ(x),注意到右边是求和,那么你可以自己计算 j=0 到 j=n 的和。但换另一种方式来想想,把hθ(x)看作θTX,那么你就可以写成两个向量的内积,其中θ就是θ0,θ1,θ2。如果你有两个特征量,如果n=2,并且如果你把x看作x0、x1、x2,这两种思考角度,会给你两种不同的实现方式。
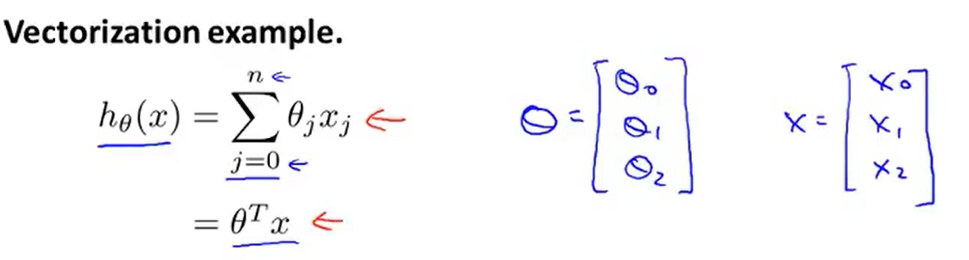 下面是未向量化的代码。未向量化的意思是没有向量化。
下面是未向量化的代码。未向量化的意思是没有向量化。

首先,我们初始化变量prediction的值为0.0,而这个变量prediction的最终结果就是hθ(x),然后我要用一个for 循环,j 从1取值到n+1,变量prediction每次就通过自身加上θjxj的值,这个就是算法的代码实现。顺便我要提醒一下,之前的向量我用的下标是0,所以我有θ0,θ1,θ2,但因为MATLAB的下标从1开始,在MATLAB 中θ0可能会用θ1 来表示,这些元素最后就会变成θ1,θ2,θ3表示,因为MATLAB中的下标从1开始,这就是为什么这里我的for循环,j从1取值到n+1,而不是从0取值到n。这是一个未向量化的代码实现方式,我们用一个for循环对n个元素进行加和。
作为比较,接下来是向量化的代码实现:
 你把x和θ看作向量,而你只需要令变量prediction等于θTX,你就可以这样计算。与其写所有这些for循环的代码,你只需要一行代码,这行代码就是利用Octave 的高度优化的数值线性代数算法来计算x和θ这两个向量的内积,这样会使代码更简单,运行起来也将更加高效。这就是Octave 所做的而向量化的方法,在其他编程语言中同样可以实现。
你把x和θ看作向量,而你只需要令变量prediction等于θTX,你就可以这样计算。与其写所有这些for循环的代码,你只需要一行代码,这行代码就是利用Octave 的高度优化的数值线性代数算法来计算x和θ这两个向量的内积,这样会使代码更简单,运行起来也将更加高效。这就是Octave 所做的而向量化的方法,在其他编程语言中同样可以实现。
让我们来看一个C++ 的例子:
 这是未向量化的代码。同样地,也是先初始化一个变量,然后再利用for循环。
这是未向量化的代码。同样地,也是先初始化一个变量,然后再利用for循环。
下面是向量化的代码实现:
 与此相反,使用较好的C++数值线性代数库,你可以写出像这样的代码,因此取决于你的数值线性代数库的内容。你或许有个C++对象:向量θ和一个C++对象:向量x。你只需要在C++中将两个向量相乘。根据你所使用的数值和线性代数库的使用细节的不同,你最终使用的代码表达方式可能会有些许不同,但是通过一个库来计算内积,你可以得到一段更简单、更有效的代码。
与此相反,使用较好的C++数值线性代数库,你可以写出像这样的代码,因此取决于你的数值线性代数库的内容。你或许有个C++对象:向量θ和一个C++对象:向量x。你只需要在C++中将两个向量相乘。根据你所使用的数值和线性代数库的使用细节的不同,你最终使用的代码表达方式可能会有些许不同,但是通过一个库来计算内积,你可以得到一段更简单、更有效的代码。
现在,让我们来看一个更为复杂的例子,这是线性回归算法梯度下降的更新规则: 我只是用θ0,θ1,θ2来写方程,假设我们有两个特征量,所以n=2,这些都是我们需要对θ0,θ1,θ2来进行更新,这些都应该是同步更新。
我只是用θ0,θ1,θ2来写方程,假设我们有两个特征量,所以n=2,这些都是我们需要对θ0,θ1,θ2来进行更新,这些都应该是同步更新。
实现这三个方程的方法就是使用一个for循环,让 j 等于0、1、2来更新对象θj。
但让我们用向量化的方式来实现,看看我们是否能够有一个更简单的方法,看看能不能一次实现这三个方程。让我们来看看怎样能压缩成一行向量化的代码来实现。思路如下:我打算把θ看做一个向量,然后我用θ-α 乘以某个别的向量δ 来更新θ。这里的δ等于(1/m)Σ(hθ(xi)-yi)xi。
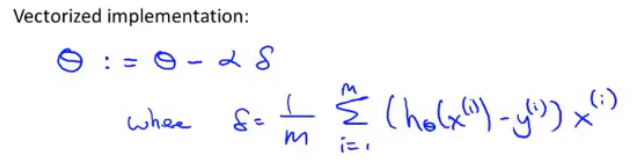 让我解释一下是怎么回事:我要把θ看做一个n+1维向量,α是一个实数,δ是一个向量。
让我解释一下是怎么回事:我要把θ看做一个n+1维向量,α是一个实数,δ是一个向量。
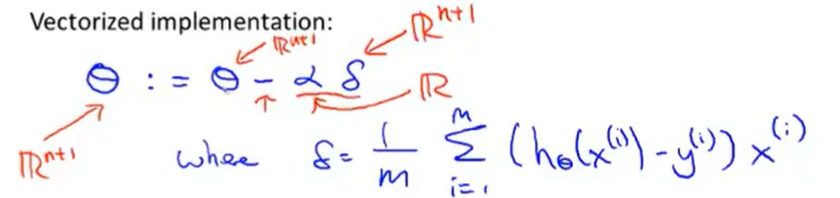 所以这个减法运算是一个向量减法,因为αδ是一个向量,所以θ更新为θ-αδ。那么向量δ是什么呢?
所以这个减法运算是一个向量减法,因为αδ是一个向量,所以θ更新为θ-αδ。那么向量δ是什么呢?
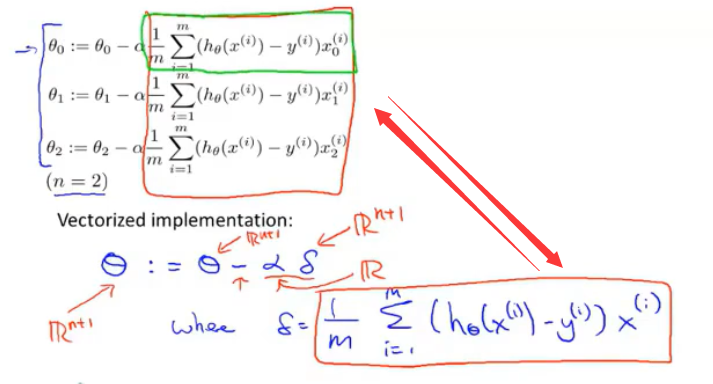 其实δ代表的就是红框框起来的内容。具体地说,δ是一个n+1维向量。向量δ的第一个元素就等于绿框框起来的内容。
其实δ代表的就是红框框起来的内容。具体地说,δ是一个n+1维向量。向量δ的第一个元素就等于绿框框起来的内容。
 认真看一下计算δ的正确方式。
认真看一下计算δ的正确方式。
 前面是一个实数,后面是一个n+1维向量。然后再求和。
前面是一个实数,后面是一个n+1维向量。然后再求和。
实际上,如果你要解下面这个方程,我们为了向量化这段代码,我们会令u = 2v +5w因此,我们说向量u等于2乘以向量v加上5乘以向量w。
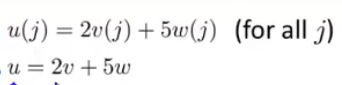
用这个例子说明,如何对不同的向量进行相加,这里的求和是同样的道理。在这个求和公式中,只是一个实数乘以一个向量x1,就像上面的2乘以向量v。然后再加上实数乘以一个向量x2,就像上面的5乘以向量w。以此类推,再加上许多项实数乘以向量。这就是为什么这一整个是一个向量δ的原因。具体而言,如果n=2,那么δ就由三项相加而组成。这就是为什么根据θ-αδ更新θ的时候可以实现同步更新。
这就是为什么我们能够向量化地实现线性回归。所以,保证你确实能理解上面的步骤。如果你实在不能理解它们数学上等价的原因,你就直接实现这个算法,也是能得到正确答案的,你仍然能实现线性回归算法。如果你能弄清楚为什么这两个步骤是等价的,那我希望你可以对向量化有一个更好的理解。
如果你在实现线性回归的时候,使用一个或两个以上的特征量。有时我们使用几十或几百个特征量来计算线性回归,当你使用向量化地实现线性回归时,通常运行速度就会比你以前用你的for循环快的多。因此使用向量化实现方式,你应该是能够得到一个高效得多的线性回归算法。而当你向量化我们将在之后的课程里面学到的算法,这会是一个很好的技巧,无论是对于Octave 或者一些其他的语言,如C++、Java 来让你的代码运行得更高效。
最后附上有中文字幕视频的链接:https://www.bilibili.com/video/BV164411b7dx/?p=31



 浙公网安备 33010602011771号
浙公网安备 33010602011771号