[斯坦福大学2014机器学习教程笔记]第二章-代价函数的数学定义
在这节,我们将定义代价函数的概念,这有助于我们弄清楚怎么样将最有可能的直线与数据相拟合。
下面我们看一个例子。

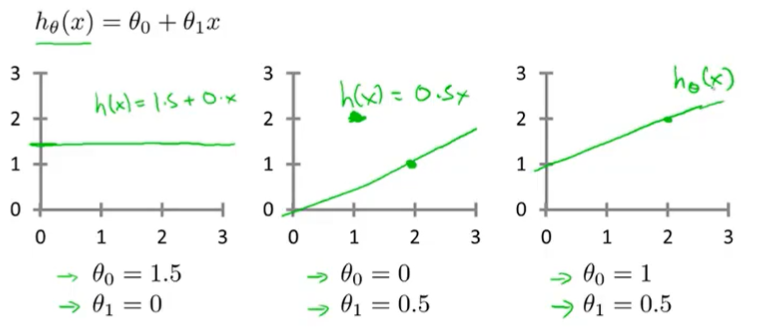
在线性回归中,我们有这样一个训练集。根据上一节的定义,我们知道m=47,而我们的假设函数的函数形式为 hθ(x)=θ0+θ1x。这些θi被称为模型参数。而我们要做的就是如何选择这两个参数值θ0和θ1。选择不同的θ0和θ1,我们会得到不同的假设函数(如下图)。
在线性回归中,我们有一个训练集,我们要得出θ0和θ1这两个参数值,来得出假设函数所表示的直线,这个直线要尽量地与这些数据点很好的拟合,也许如下图这条直线一样。
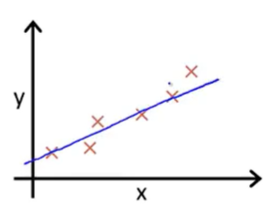
那么,我们怎么得出θ0和θ1的值呢?怎么使得出的直线很好地拟合数据呢?
我们的想法是:我们要选择输入x时我们预测的值最接近该样本对应的y值的参数θ0和θ1。所以,在我们的训练集中我们会得到一定数量的样本。在之前的例子中,我们知道x表示卖出那所房子并知道这所房子的实际卖出价格。所以我们要尽量选择参数值使得我们能够合理准确预测y的值。
在线性回归中,我们要解决的是一个最小化的问题。所以我要写出关于θ0和θ1的最小化,而且我希望h(x)-y这个式子的值要尽量小,即我要做的事情就是尽量减少假设输出的价格与房子真实的价格之间的差的平方。
我想要做的事是对i=1到i=m的样本,将对假设进行预测得到的结果减去实际价格所得到的差的平方相加(即Σ(hθ(xi)-yi)2)。也就是预测值和实际值的差的平方误差和或者说预测价格和。我希望尽量减少这个值。实际上我们考虑的是(1/m)Σ(hθ(xi)-yi)2即平均误差。前面这些只是为了是数学更直白一些,因此对这个求和值的二分之一求最小值。
实际上,我们的目标是求出θ0和θ1的值使(1/2m)Σ(hθ(xi)-yi)2最小。因此,我们线性回归的代价函数为J(θ0,θ1)=(1/2m)Σ(hθ(xi)-yi)2。我们想要做的就是关于θ0和θ1对函数J(θ0,θ1)求最小值。
代价函数也被称为平方误差函数,有时也被称为平方误差代价函数。事实上我们之所以要求出误差的平方和,是因为误差平方代价函数对大多数问题,特别是回归问题都是一个合理的选择。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号