OO第三次单元总结

一：JML的理论基础

1.基本概念

JML(Java Modeling Language)是用于对Java程序进行规格化设计的一种表示语言。JML是一种行为接口规格语言 （Behavior Interface Specification Language，BISL），基于Larch方法构建。BISL提供了对方法和类型的规格定义 手段。所谓接口即一个方法或类型外部可见的内容。JML主要由Leavens教授在Larch上的工作，并融入了Betrand Meyer， John Guttag等人关于Design by Contract的研究成果。近年来，JML持续受到关注，为严格的程序设计提供 了一套行之有效的方法。通过JML及其支持工具，不仅可以基于规格自动构造测试用例，并整合了SMT Solver等工具 以静态方式来检查代码实现对规格的满足情况。

2.注释结构

JML以javadoc注释的方式来表示规格，每行都以@起头。有两种注释方式，行注释和块注释。其中行注释的表示方式 为 //@annotation ，块注释的方式为 /* @ annotation @*/ 。

3.JML表达式

2.1原子表达式

原子表达式包括以下几种：

\result表达式

\old（expr）表达式

\not_assigned(x,y,...)表达式

\not_modified(x,y,...)表达式

\nonnullelements( container )表达式

\type(type)表达式

\typeof(expr)表达式

2.2量化表达式

\forall表达式：全称量词修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。 (\forall int i,j; 0 <= i && i < j && j < 10; a[i] < a[j]) ，意思是针对任意 0<=i<j<10，a[i]<a[j] 。这个表达式如果 为真( true )，则表明数组a实际是升序排列的数组。

\exists表达式：存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。 (\exists int i; 0 <= i && i < 10; a[i] < 0) ，表示针对0<=i<10，至少存在一个a[i]<0。

\sum表达式：返回给定范围内的表达式的和。 (\sum int i; 0 <= i && i < 5; i) ，这个表达式的意思计算[0,5) 范围内的整数i的和，即0+1+2+3+4==10。注意中间的 0 <= i && i < 5 是对i范围的限制，求和表达式为最后面的 那个 i 。同理，我们构造表达式 (\sum int i; 0 <= i && i < 5; i*i) ，则返回的结果为1+4+9+16。

\product表达式：返回给定范围内的表达式的连乘结果。 (\product int i; 0 < i && i < 5; i) ，这个表达式的 意思是针对(0,5)范围的整数的连乘结果，即1* 2* 3 * 4==24。

 \max表达式：返回给定范围内的表达式的最大值。 (\max int i; 0 <= i && i < 5; i) ，这个表达式返回[0,5)中 的最大的整数，即4。

 \min表达式：返回给定范围内的表达式的最小值。 (\min int i; 0 <= i && i < 5; i) ，这个表达式返回[0,5)中 的最小的整数，即0。

 \num_of表达式：返回指定变量中满足相应条件的取值个数。 (\num_of int x; 0<=20;x%2==0) ，这个表 达式给出(0,20]以内能够被2整除的整数个数，得到的数目为10。一般的，\num_of表达式可以写成 (\num_of T x; R(x);P(x)) ，其中T为变量x的类型，R(x)为x的取值范围；P(x)定义了x需要满足的约束条件。从逻辑上来看，该表达 式也等价于 (\sum T x;R(x)&&P(x);1) 。

2.3集合表达式

集合构造表达式：可以在JML规格中构造一个局部的集合（容器），明确集合中可以包含的元素。 new JMLObjectSet {Integer i | s.contains(i) && 0 < i.intValue() } 表示构造一个JMLObjectSet对象，其中 包含的元素类型为Integer，该集合中的所有元素都在容器集合s中出现（注：该容器集合指Java程序中构建的容器， 比如ArrayList），且整数值大于0。集合构造表达式的一般形式为：new ST {T x|R(x)&&P(x)}，其中的R(x)对应集合 container != null && (\forall int i; 0 <= i && i < container.length; container[i] != null) 1 2 3 中x的范围，通常是来自于某个既有集合中的元素，如s.has(x)，P(x)对应x取值的约束。

2.4操作符

操作符包括

(1) 子类型关系操作符： E1<E2，如果类型E1是E2的子类型则表达式结果为真，否则为假。

(2) 等价关系操作符： b_expr1<==>b_expr2 或者 b_expr1<=!=>b_expr2 ，其中b_expr1和b_expr2都是布尔表达 式，这两个表达式的意思是 b_expr1==b_expr2 或者 b_expr1!=b_expr2 。

(3) 推理操作符： b_expr1==>b_expr2 或者 b_expr2<==b_expr1 。对于表达式 b_expr1==>b_expr2 而言，当 b_expr1==false ，或者 b_expr1==true 且 b_expr2==true 时，整个表达式的值为 true。

4.方法规格

方法规格的核心内容包括 三个方面，前置条件、后置条件和副作用约定。

JML一般都有requires子句作为前置条件、副作用范围限定nothing作为副作用和ensures子句作为后置条件。requires子句是定义该方法的前置条件，这是对调用者的一些要求，如果想要调用这个方法来得到预计的结果的话，那么需要满足requires子句中的条件才可以；副作用范围nothing，这个是列出这个方法执行后，会对哪些类成员进行修改，\nothing代表不会对任何成员进行修改，也表示是个pure方法；ensures子句定义后置条件，这是对方法实现的要求，这个方法要是的ensures后面的子句条件为真。需要注意的是，规格中的每个子句必须以分号结尾。

5.类型规格

不变式（invariant）是要求在所有可见状态下都必须满足的特性，语法上定义 invariant P ，其中 invariant 为关 键词， P 为谓词。对于类型规格而言，可见状态(visible state)是一个特别重要的概念。下面所述的几种时刻下对象 o的状态都是可见状态：

对象的有状态构造方法（用来初始化对象成员变量初值）的执行结束时刻

在调用一个对象回收方法(finalize方法)来释放相关资源开始的时刻

在调用对象o的非静态、有状态方法(non-helper)的开始和结束时刻

在调用对象o对应的类或父类的静态、有状态方法的开始和结束时刻

在未处于对象o的构造方法、回收方法、非静态方法被调用过程中的任意时刻

在未处于对象o对应类或者父类的静态方法被调用过程中的任意时刻

状态变化约束constraint

对象的状态在变化时往往也许满足一些约束，这种约束本质上也是一种不变式。JML为了简化使用规则，规定 invariant只针对可见状态(即当下可见状态)的取值进行约束，而是用constraint来对前序可见状态和当前可见状态的 关系进行约束。

 

二：JMLUnitNG测试：

我使用了JMLnitNG进行相关的形式化验证

 

 

三：作业架构：

第一次作业在一开始我并没有进行过多的关于数据结构的处理，仅仅是根据JML所进行的规格描述进行处理完成其所具备的最基础的功能，在都是使用Arratlist进行处理，这也导致了中测出现TLE的情况，而在认识到这个问题之后，我又使用了HAHSMAP进行处理，这样可以使得中测的点全过。但是在强测中，仍然出现了较多的TLE的情况，因此，我认识到这是重复处理点的情况，在每次addpath的时候都对每个path进行了重复处理，这样会导致超时的情况。因此，我引入了新的数据结构nodeall对点进行处理存储。

 

 

 

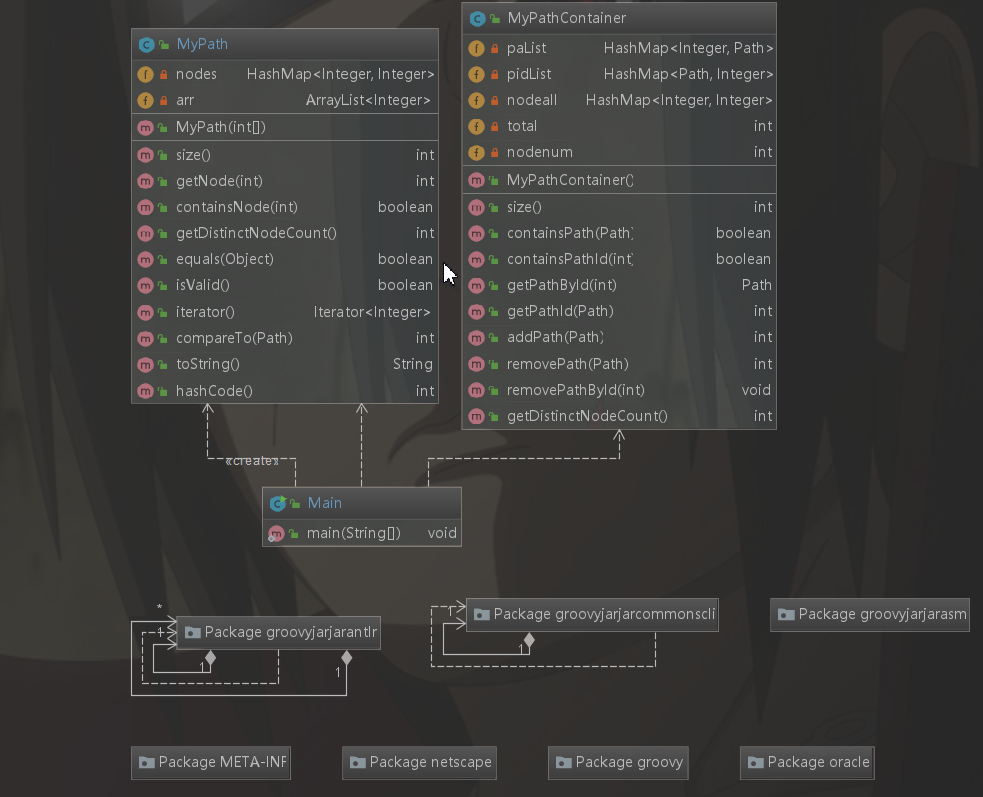
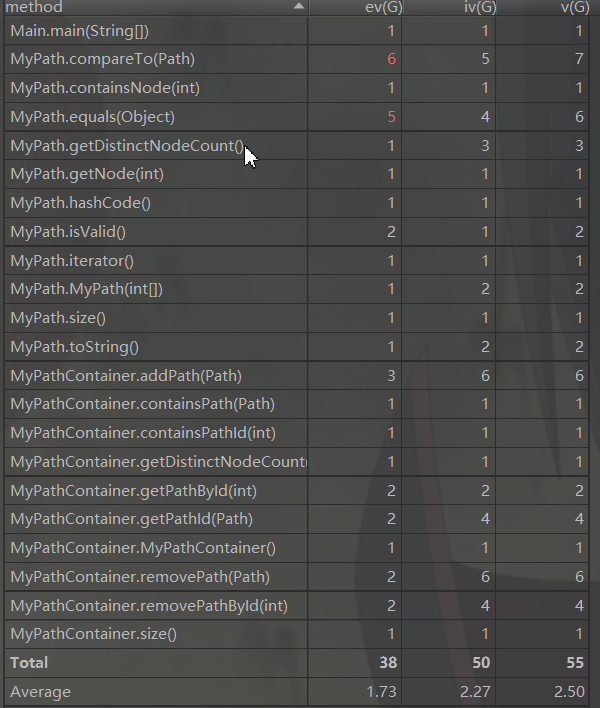
第二次作业中，我引入了一个map的二维数组图结构，用于存储每个节点之间的关系，又引入了dis的二维数组图结构，用于存储每个点之间的距离。同时nodetomap，存储每个出现过的点对应的图下标，从而将所有的映射到图上之后，之后使用了floyd算法求出了每个点之间的最短路径，从而完成了作业要求。

 

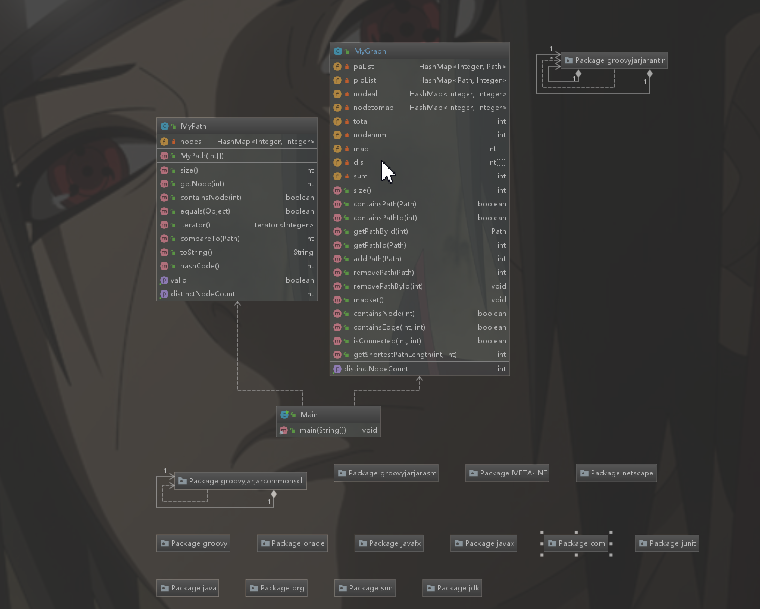
第三次作业中，我们使用了一种简化了的算法，避免了将每条路径中结点信息存入，而是将换乘每条路径的赋予其换乘的权重，在之后减去我们所赋予的权重。即例如，在计算最低票价时，对每条Path, 任意两个直接连边，边权x+2y，即在边权中直接加入换乘的钱，然后在运行floyd。对于每条边的信息收集，我们单独使用floyd运算，并将其结果存储在自己创建的类Pathdeal中以便重复使用，减少运算的复杂度。并我们分别对于每种需求单独开一个二维静态数组的图结构。

 

 

 

 

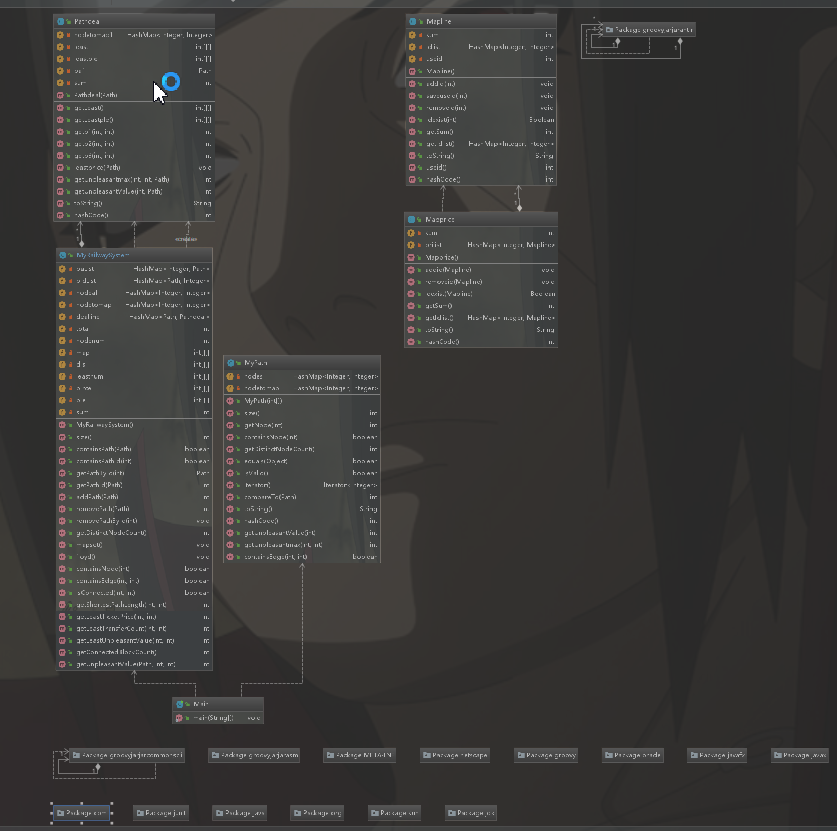
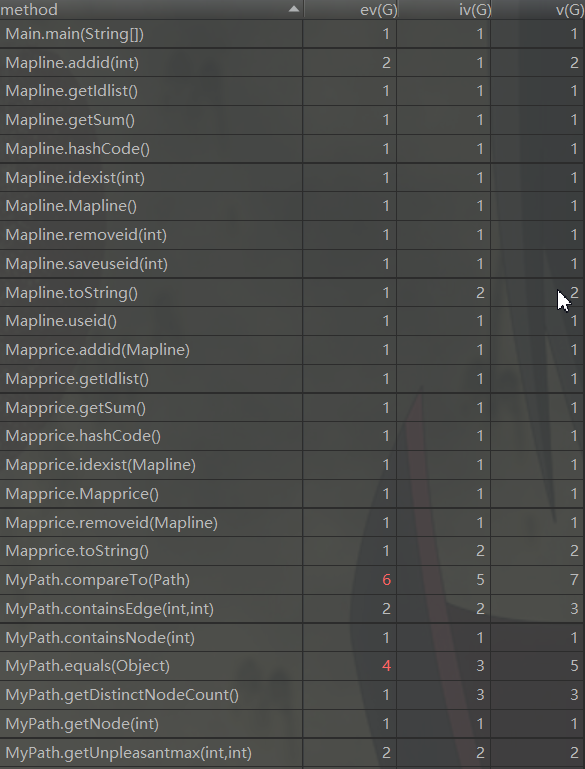
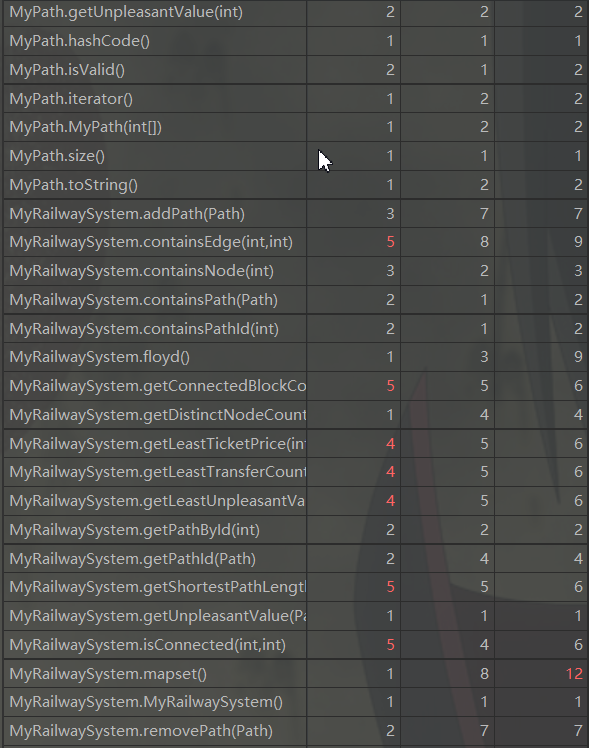
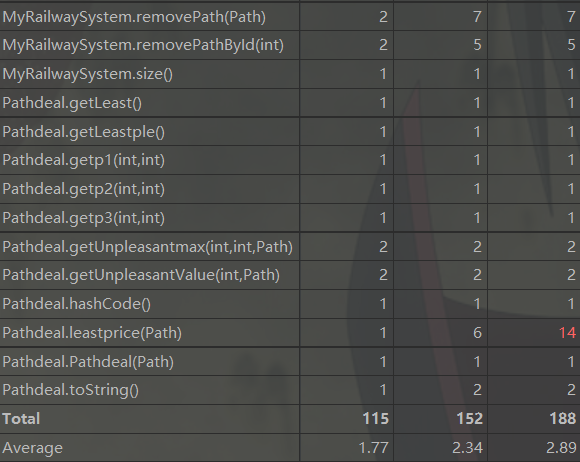
四：bug分析

在这几次的作业过程中，我的程序里面出现了很多的bug（尤其是在前两次）。在第一次作业中，我的compareto里面由于理解不是特别到位导致其中出现了bug，所使用的结构也导致了tle情况的出现。在第二次作业中，我出现了对于重复出现的点不能够重复利用所拥有的内存的情况，这直接导致了在remove之后添加path结点会出现数组越界的情况。在第三次作业中，还存在着对于静态数组把握不到位所导致了数组越界的情况的出现，这些bug数量之多是在之前几次作业中我没有出现过的。

 

 

五：思想感悟：

在这个单元的作业过程中，主要是让我们学会了如何使用JML这一规格工具的使用方法，让我们体会到规格这一程序设计的思想，同时在三次作业中加入了关于各种类型的数据结构的思想，必须要使用各种有关图的处理方法才能够较好的完成这三次作业，而这也极大的提升了我们的工程化能力。同时，我们在写作业的过程中也加入了各种工程化验证的方法，这也极大的提升了我们检验程序鲁棒性的能力。但是，我个人认为这个单元的规划化设计所占的比重并不是想象中的那么大，而是作业所要求实现的数据结构占着很大的比重，需要花很大的精力去实现所要求的复杂数据结构。