算法

递归算法

1. 调用本身
2. 结束条件

#递归循环

1. 正常顺序循环

#print在前,先print3然后开始递归,递归到最里层开始跳出,结束
def fun3(x):
    if x>0:
　　　　 print(x)
        fun3(x-1)
fun3(3)　　#3 2 1

1. 逆循环

#循环到最里层的1后，开始一步步向外层跳出,跳出一步执行一次print
def fun3(x):
    if x>0:
        fun3(x-1)
        print(x)
fun3(3)　　#1 2 3

 时间复杂度

 

 

二分查找

#顺序查找循环
def linear_search(data_set,value):
　　for i in range(range(data_set)):
　　　　if data_set[i]==value:
　　　　　　return i
　　return
#二分循环
def bin_search(data_set,value)
　　low=0
　　high=len(data_set)-1

 

 

 

方差标准差的意义是什么？它们有何特性？

一、标准差它反映组内个体间bai的离散程度。具有两种特性：
测量到分布程度的结果为非负数值，与测量资料具有相同单位。

一个总量的标准差或一个随机变量的标准差，及一个子集合样品数的标准差之间，有所差别。简单来说，标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。

标准差可以当作不确定性的一种测量。

例如在物理科学中，做重复性测量时，测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值，测量值的标准差占有决定性重要角色：

如果测量平均值与预测值相差太远（同时与标准差数值做比较），则认为测量值与预测值互相矛盾。这很容易理解，因为如果测量值都落在一定数值范围之外，可以合理推论预测值是否正确。

二、方差它反映用来度量随机变量和其数学期望（即均值）之间的偏离程度。具有特性如下
1、设C是常数，则D（C）=0

2、设X是随机变量，C是常数，则有 

 

 

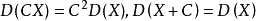
3、设 X 与 Y 是两个随机变量，则

 

 

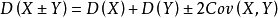
其中协方差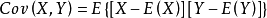 

 

特别的，当X，Y是两个不相关的随机变量则

 

 

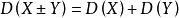
此性质可以推广到有限多个两两不相关的随机变量之和的情况。