机器学习数学基础 - 概率论

随机事件和概率

基础概念

░  随机试验

░  样本点和样本空间

░  随机事件

随机事件的概率

░  例子

条件概率

░  定义

P (B|A) 表示 在 A 条件下的 B 发生的概率

P (AB)  表示 AB 其实就是 A ∩ B  , 及 A B 同时发生的概率

如果 A , B 相互独立,  则 P(AB)=P(A) * P(B)

如果 A, B 不是相互独立,  则 P(AB)=P(B|A) * P(A) 即 全概率公式 

如果相互独立 , 则 P(B|A) = P(AB) / P(A) = P(A) * P(B) / P(A) = P(B) 

░  例子

事件的独立性

░  定义

░  例子

全概率公式和贝叶斯公式

全概率公式

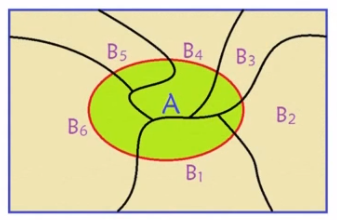
如图所示, 全绿色的区域可以理解为 A 于 B1-6 之间交叠部分的叠加, 及在A 条件下 B1-6 发生的可能性的集和

由此表示全概率公式

贝叶斯公式

在上图中的 P(x) 表示 任何一个样本发生的概率, 这里的 P(x) 和 期望求的参数 θ 是无关的,  即于这个系统是无关的, 当做是一个常数来处理

因此在上面的推导下,  P(θ|x) 于 P(θ|x) P(θ) 是一个正比的关系

而这样  P(θ) 是先验概率, P(θ|x) 是后验概率,  P(x|θ) 是似然函数

 实例

随机变量, 期望和方差

随机变量

░  定义

░  例子

概率分布

░  定义

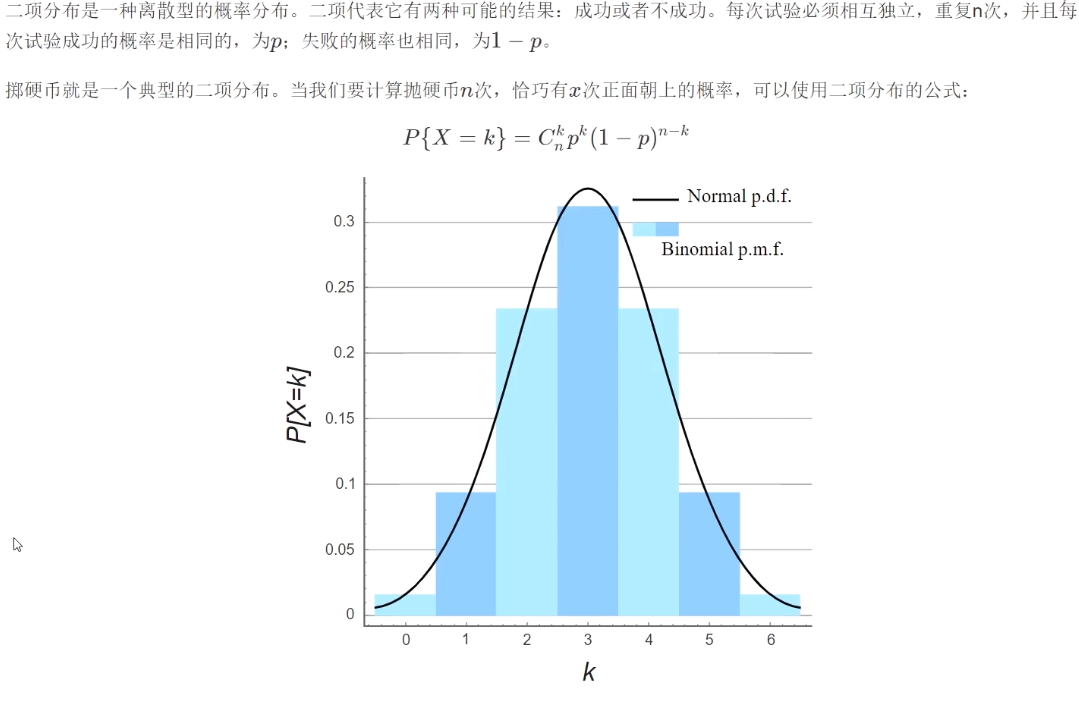
░  性质

 

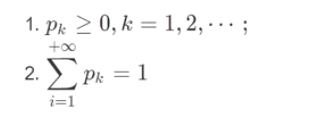
░  二项分布

░  负二项分布

 

 

负二项分布是基于二项分布的分支, 这里反着想, 持续实验直到 r次成功计算 试验次数x的概率

可以保证的是最后一次一定成功, 因此 r-1 以及 x-1 然后计算概率

由此的使用场景如下

░  泊松分布

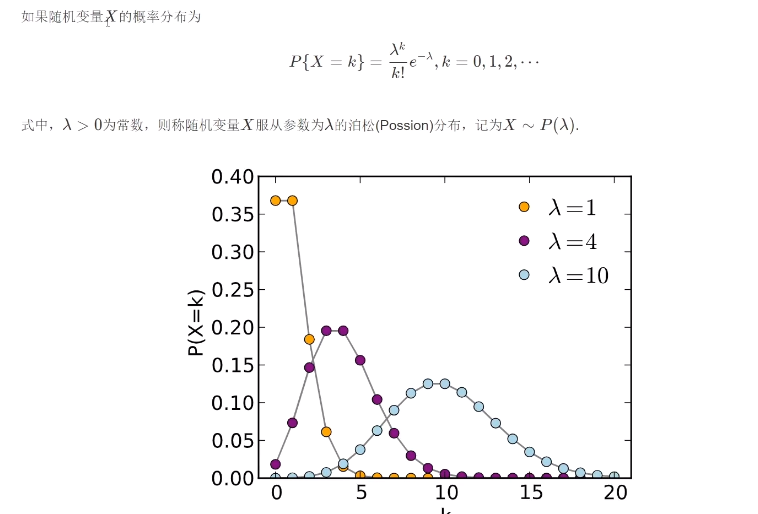
概率密度函数

░  定义

░  正态分布

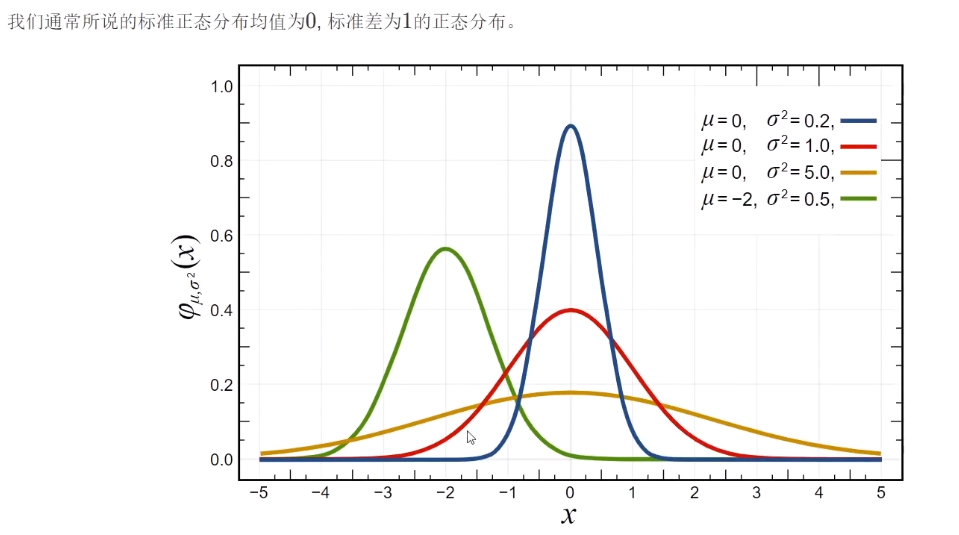
分布总结

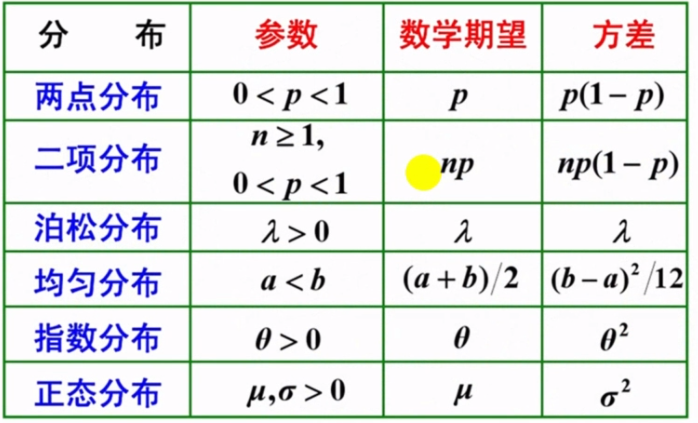
随机变量的期望

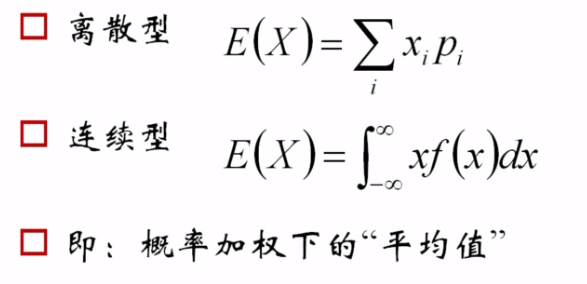
░  正态性质

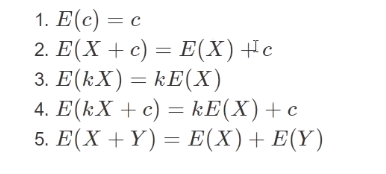
░  例子

随机变量的方差

░  定义

░  性质

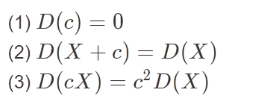
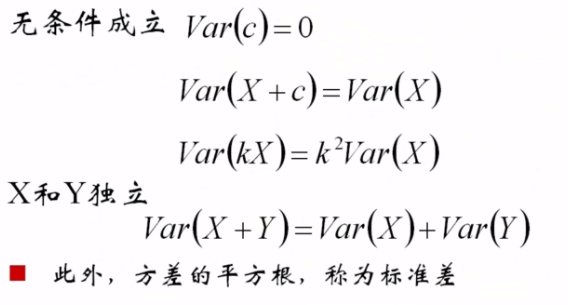
░  例子

协方差

░  定义

░  公式性质

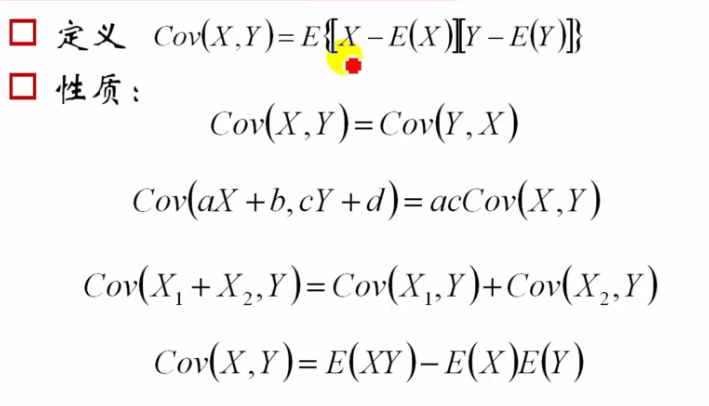
░  独立 / 不相干 定义

░  协方差的上界

░  协方差矩阵

最大似然估计

定义

概率 / 统计

最大似然估计

例子

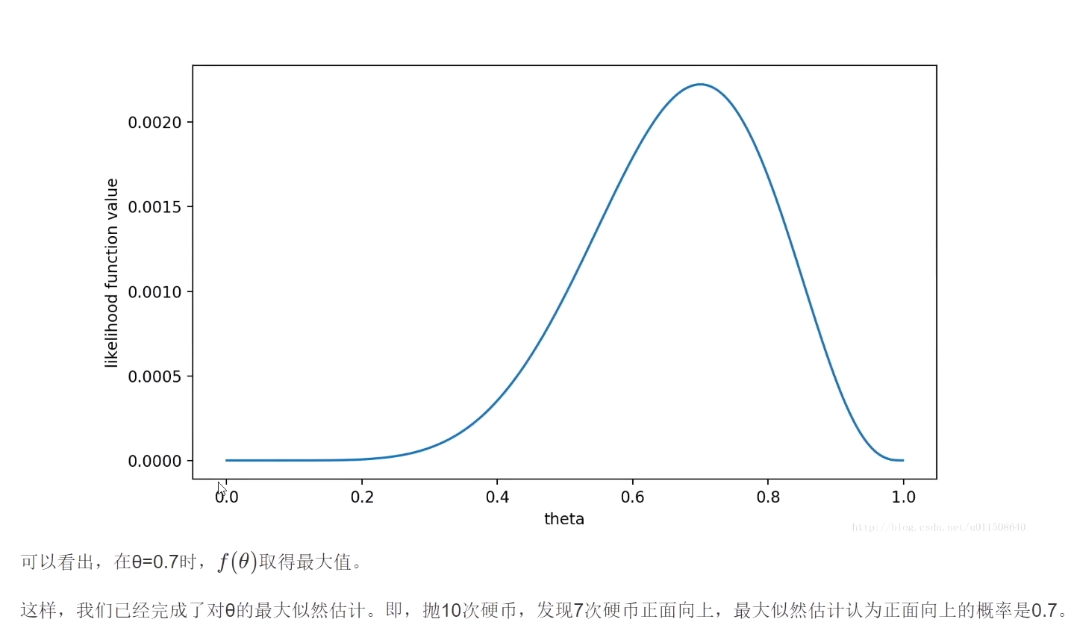
 总结