我的icpc模板(更新中)
是时候整点模板了
整数三分
int l = 1,r = 100; while(l < r) { int lmid = l + (r - l) / 3; // l + 1/3区间大小 int rmid = r - (r - l) / 3; // r - 1/3区间大小 lans = cal(lmid),rans = cal(rmid); // 求凹函数的极小值 if(lans <= rans) r = rmid - 1; else l = lmid + 1; // 求凸函数的极大值 if(lasn >= rans) l = lmid + 1; else r = rmid - 1; } // 求凹函数的极小值 cout << min(lans,rans) << endl; // 求凸函数的极大值 cout << max(lans,rans) << endl;
浮点数三分
const double EPS = 1e-9; while(r - l < EPS) { double lmid = l + (r - l) / 3; double rmid = r - (r - l) / 3; lans = cal(lmid),rans = cal(rmid); // 求凹函数的极小值 if(lans <= rans) r = rmid; else l = lmid; // 求凸函数的极大值 if(lans >= rans) l = lmid; else r = rmid; } // 输出 l 或 r 都可 cout << l << endl;
bsgs
ll BSGS(ll a, ll b, ll m) { static map<ll, ll> hs; hs.clear(); ll cur = 1, t = sqrt(m) + 1; for (int B = 1; B <= t; ++B) { (cur *= a) %= m; hs[b * cur % m] = B; // 哈希表中存B的值 } ll now = cur; // 此时cur = a^t for (int A = 1; A <= t; ++A) { auto it = hs.find(now); if (it != hs.end()) return A * t - it->second; (now *= cur) %= m; } return -1; // 没有找到,无解 }
字符串哈希
#include<bits/stdc++.h> #define fi first #define se second #define lowbit(x) (x&(-x)) using namespace std; typedef pair<int,int> pii; typedef long long ll; typedef unsigned long long ull; typedef pair<ull,ull> puu; const ull mod1=19260817; const ull mod2=19660813; const ull base=233; puu gethash(string &s){ ull ans1=0ll,ans2=0ll; for(auto i:s){ ans1=(ans1*base+ull(i))%mod1; ans2=(ans2*base+ull(i))%mod2; } return {ans1,ans2}; } void solve(){ int n;cin>>n;vector<puu>a(n+1); for(int i=1;i<=n;i++){ string s;cin>>s; a[i]=gethash(s); } int ans=1; sort(a.begin()+1,a.end()); for(int i=2;i<=n;i++) if(a[i]!=a[i-1])ans++; cout<<ans<<"\n"; } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); srand((unsigned)time(NULL)); //int t;std::cin>>t;while(t--) solve(); }
线段树维护字符串哈希,以及回文
#include<bits/stdc++.h> #define fi first #define se second #define lowbit(x) (x&(-x)) #define lson l,mid,k<<1 #define rson mid+1,r,k<<1|1 #define fa #define lt k<<1 #define rt k<<1|1 using namespace std; typedef pair<int,int> pii; typedef long long ll; typedef unsigned long long ull; typedef pair<ull,ull> puu; const ull mod1=19260817; const ull mod2=19660813; const ull base=233; const int N=1e6+10; typedef pair<int,int> pii; ull pw1[N],pw2[N]; void initpw(){ pw1[0]=pw2[0]=1; for(int i=1;i<=1e6;i++){ pw1[i]=pw1[i-1]*base%mod1; pw2[i]=pw2[i-1]*base%mod2; } } struct segtree{ puu hash1,hash2;//分别表示正与逆 ull len; char c; segtree operator +(const segtree &B){ segtree res; res.len=len+B.len; res.hash1={(hash1.fi*pw1[B.len]%mod1+B.hash1.fi)%mod1,(hash1.se*pw2[B.len]%mod2+B.hash1.se)%mod2}; res.hash2={(B.hash2.fi*pw1[len]%mod1+hash2.fi)%mod1,(B.hash2.se*pw2[len]%mod2+hash2.se)%mod2}; return res; } }seg[N<<2]; puu gethash(char c){ return {c*base%mod1,c*base%mod2}; } bool ispal(segtree B){ return B.hash1==B.hash2; } void build(int l,int r,int k){ if(l==r){ cin>>seg[k].c; seg[k].hash1=seg[k].hash2=gethash(seg[k].c); seg[k].len=1; return ; } int mid=l+r>>1; build(lson),build(rson); seg[k]=seg[lt]+seg[rt]; } void update(int l,int r,int k,int x,char z){ if(l==r){ seg[k].c=z; seg[k].hash1=seg[k].hash2=gethash(seg[k].c); return ; } int mid=l+r>>1; if(x<=mid)update(lson,x,z); if(x>mid)update(rson,x,z); seg[k]=seg[lt]+seg[rt]; } segtree query(int l,int r,int k,int x,int y){ if(x<=l&&r<=y)return seg[k]; segtree res;res.len=0;res.hash1={0ull,0ull};res.hash2={0ull,0ull}; int mid=l+r>>1; if(x<=mid)res=res+query(lson,x,y); if(y>mid)res=res+query(rson,x,y); return res; } void solve(){ int n,m;cin>>n>>m; build(1,n,1); while(m--){ int op;cin>>op; if(op==1){ int x;char z;cin>>x>>z; update(1,n,1,x,z); } else{ int x,y;cin>>x>>y; auto temp=query(1,n,1,x,y); if(ispal(query(1,n,1,x,y)))cout<<"Yes\n"; else cout<<"No\n"; } } } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); srand((unsigned)time(NULL)); initpw(); //int t;std::cin>>t;while(t--) solve(); }
图论 tarjan
求强连通分量。sccnt为强联通分量的数量。newe为缩点后的边。
#include<bits/stdc++.h> #define fi first #define se second #define lowbit(x) (x&(-x)) #define int long long #define ll long long using namespace std; void solve(){ int n,m;cin>>n>>m; vector<vector<int>>e(n+1); vector<int>dfsn(n+1),low(n+1),instk(n+1),scc(n+1); stack<int>stk; while(m--){ int u,v;cin>>u>>v; e[u].push_back(v); } int dfscnt=0,sccnt=0; function<void(int)>tarjan=[&](int u){ low[u]=dfsn[u]=++dfscnt; instk[u]=1; stk.push(u); for(auto v:e[u]){ if(!dfsn[v]){ tarjan(v); low[u]=min(low[u],low[v]); } else if(instk[v])low[u]=min(low[u],dfsn[v]); } if(low[u]==dfsn[u]){ int temp; do{ temp=stk.top(); stk.pop(); instk[temp]=0; scc[temp]=sccnt; }while(temp!=u); sccnt++; } }; for(int i=1;i<=n;i++)if(!dfsn[i])tarjan(i); vector<vector<int>>newe(sccnt); for(int i=1;i<=n;i++) for(auto j:e[i]) if(scc[j]!=scc[i]) newe[scc[i]].push_back(scc[j]); } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); //srand((unsigned)time(NULL)); //int t;std::cin>>t;while(t--) solve(); }
求双连通分量
注意到,无向图中不存在横着的边。
#include<bits/stdc++.h> #define fi first #define se second #define lowbit(x) (x&(-x)) using namespace std; typedef pair<int,int> pii; void solve(){ int n,m;cin>>n>>m; vector<vector<pii>>e(n+1); while(m--){ int u,v,w;cin>>u>>v>>w; e[u].emplace_back(v,w); e[v].emplace_back(u,w); } vector<int>dfsn(n+1),low(n+1),instk(n+1),scc(n+1); stack<int>stk; int dfscnt=0,sccnt=0; function<void(int,int)>tarjan=[&](int u,int fa){ dfsn[u]=low[u]=++dfscnt; instk[u]=1; stk.push(u); for(auto v:e[u]){ if(v.fi==fa)continue; if(!dfsn[v.fi]){ tarjan(v.fi,u); low[u]=min(low[u],low[v.fi]); } else if(instk[v.fi])low[u]=min(low[u],dfsn[v.fi]); } if(dfsn[u]==low[u]){ int temp; do{ temp=stk.top(); stk.pop(); instk[temp]=0; scc[temp]=sccnt; }while(temp!=u); sccnt++; } }; for(int i=1;i<=n;i++)if(!dfsn[i])tarjan(i,0); vector<int>col(sccnt); vector<vector<pii>>newe(sccnt); for(int i=1;i<=n;i++) for(auto j:e[i]){ if(scc[i]==scc[j.fi]){ if(j.se)col[scc[i]]=1; } else{ newe[scc[i]].emplace_back(scc[j.fi],j.se); } } int x,y;cin>>x>>y; x=scc[x];y=scc[y]; if(x==y){ if(col[x])cout<<"YES\n"; else cout<<"NO\n"; return ; } int flag=0; function<void(int,int,int)>dfs=[&](int u,int f,int fa){ f|=col[u]; if(u==y){ if(f){cout<<"YES\n";flag=1;return ;} } for(auto j:newe[u])if(j.fi!=fa)dfs(j.fi,f|j.se,u); }; dfs(x,0,-1); if(!flag)cout<<"NO\n"; } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); srand((unsigned)time(NULL)); //int t;std::cin>>t;while(t--) solve(); }
lucas
const int N=200010; int fect[N],infect[N]; ll inv(int x,int p){ return binpow(x,p-2ll,p); } ll C(ll a, ll b, ll p) { return a < b ? 0 : fect[a] * inv(fect[b], p) % p * inv(fect[a - b], p) % p; } int lucas(int a,int b,int p){ if(b==0)return 1; return (lucas(a/p,b/p,p)*C(a%p,b%p,p))%p; } void solve(){ int n,m,p; cin>>n>>m>>p;m+=n;fect[0]=1; for(int i=1;i<=m;i++)fect[i]=(fect[i-1]*i)%p; cout<<lucas(m,n,p)<<"\n"; } signed main(){ std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0); //srand((unsigned)time(NULL)); int t;cin>>t;while(t--) solve(); }
fft
#include <bits/stdc++.h> using namespace std; inline int read() { int ans = 0; char c = getchar(); while (!isdigit(c)) c = getchar(); while (isdigit(c)) { ans = ans * 10 + c - '0'; c = getchar(); } return ans; } typedef complex<double> comp; const int MAXN = 3000005; comp A[MAXN], B[MAXN], ans[MAXN]; int rev[MAXN]; const comp I(0, 1); const double PI = acos(-1); void fft(comp F[], int N, int inv = 1) { int bit = log2(N); for (int i = 0; i < N; ++i) { rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1)); if (i < rev[i]) swap(F[i], F[rev[i]]); } for (int l = 1; l < N; l *= 2) // 枚举合并前的区间长度 { comp step = exp(inv * PI / l * I); for (int i = 0; i < N; i += l * 2) // 遍历起始点 { comp cur(1, 0); for (int k = i; k < i + l; ++k) { comp g = F[k], h = F[k + l] * cur; F[k] = g + h, F[k + l] = g - h; cur *= step; } } } if (inv == -1) for (int i = 0; i < N; ++i) F[i] /= N; } int main() { int n = read(), m = read(), N = 1 << int(log2(n + m) + 1); for (int i = 0; i <= n; ++i) A[i] = read(); for (int i = 0; i <= m; ++i) B[i] = read(); fft(A, N), fft(B, N); for (int i = 0; i < N; ++i) ans[i] = A[i] * B[i]; fft(ans, N, -1); for (int i = 0; i <= n + m; ++i) printf("%d ", int(ans[i].real() + 0.1)); return 0; }
高斯消元
线性基 bitset优化
bitset<maxn>p[maxn]; bitset<maxn>op[maxn]; vector<string>a; int n; string oo; int kk = -1; void insert(string& s, int idx) { int flag = -1; bitset<maxn>x(s); bitset<maxn>opx(oo); opx[idx] = 1; for (int i = maxn - 2; i >= 0; i--) { if (x[i]) { if (p[i].count() == 0) { flag = i; op[flag] = opx; p[flag] = x;break; } x ^= p[i]; opx ^= op[i]; } } if (x.count() == 0) { kk = 1; } return ; }
朴素线性基
vector<ull> B; void insert(ull x) { for (auto b : B) x = min(x, b ^ x); for (auto &b : B) b = min(b, b ^ x); if (x) B.push_back(x); }
莫比乌斯反演

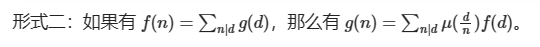
#include<bits/stdc++.h> #define N 60010 using namespace std; template<typename T>inline void read(T &x) { x=0; static int p;p=1; static char c;c=getchar(); while(!isdigit(c)){if(c=='-')p=-1;c=getchar();} while(isdigit(c)) {x=(x<<1)+(x<<3)+(c-48);c=getchar();} x*=p; } bool vis[N]; int prim[N],mu[N],sum[N],cnt; void get_mu(int n) { mu[1]=1; for(int i=2;i<=n;i++) { if(!vis[i]){mu[i]=-1;prim[++cnt]=i;} for(int j=1;j<=cnt&&i*prim[j]<=n;j++) { vis[i*prim[j]]=1; if(i%prim[j]==0)break; else mu[i*prim[j]]=-mu[i]; } } for(int i=1;i<=n;i++)sum[i]=sum[i-1]+mu[i]; } int main() { // freopen("P3455.in","r",stdin); // freopen("P3455.out","w",stdout); int t; read(t); get_mu(50000); while(t--) { static int a,b,d; read(a);read(b);read(d); static int max_rep; max_rep=min(a/d,b/d); static long long ans;ans=0; for(int l=1,r;l<=max_rep;l=r+1) { r=min((a/d)/((a/d)/l),(b/d)/((b/d)/l)); ans+=(long long)((a/d)/l)*((b/d)/l)*(sum[r]-sum[l-1]); } printf("%lld\n",ans); } return 0; }
线性基
vector<ll>B; void insert(ll x){ for(auto &b:B)x=min(x,b^x); for(auto &b:B)b=min(b,x^b); if(x)B.push_back(x); }
计算几何
namespace Geometry
{
const double pi = acos(-1);
const double eps = 1e-8;
// 点与向量
struct Point
{
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
bool operator==(const Point a) const
{
return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
}
};
typedef Point Vector;
Vector operator+(Vector A, Vector B)
{
return Vector(A.x + B.x, A.y + B.y);
}
Vector operator-(Vector A, Vector B)
{
return Vector(A.x - B.x, A.y - B.y);
}
Vector operator*(Vector A, double p)
{
return Vector(A.x * p, A.y * p);
}
Vector operator/(Vector A, double p)
{
return Vector(A.x / p, A.y / p);
}
int sign(double x)
{ // 符号函数
if (fabs(x) < eps)
return 0;
if (x < 0)
return -1;
return 1;
}
int cmp(double x, double y)
{ // 比较函数
if (fabs(x - y) < eps)
return 0;
if (x < y)
return -1;
return 1;
}
double dot(Point a, Point b)
{ // 向量点积
return a.x * b.x + a.y * b.y;
}
double cross(Point a, Point b)
{ // 向量叉积
return a.x * b.y - b.x * a.y;
}
double get_length(Point a)
{ // 求向量模长
return sqrt(dot(a, a));
}
double get_angle(Point a, Point b)
{ // 求A->B的有向角
return acos(dot(a, b) / get_length(a) / get_length(b));
}
double area(Point a, Point b, Point c)
{ // A为顶点,向量AB与向量AC的叉积,即三角形ABC的面积的2倍(有向)
return cross(b - a, c - a);
}
Point rotate(Point a, double angle)
{ // 将向量A顺时针旋转angle度
return Point(a.x * cos(angle) + a.y * sin(angle), -a.x * sin(angle) + a.y * cos(angle));
}
Point get_line_intersection(Point p, Vector v, Point q, Vector w)
{ // 两直线的交点
// 使用前提,直线必须有交点
// cross(v, w) == 0则两直线平行或者重合
Vector u = p - q;
double t = cross(w, u) / cross(v, w);
return p + v * t;
}
double distance_to_line(Point p, Point a, Point b)
{ // 点到直线的距离,直线为AB所在直线
Vector v1 = b - a, v2 = p - a;
return fabs(cross(v1, v2) / get_length(v1));
}
double distance_to_segment(Point p, Point a, Point b)
{ // 点到线段的距离,线段为线段AB
if (a == b)
return get_length(p - a);
Vector v1 = b - a, v2 = p - a, v3 = p - b;
if (sign(dot(v1, v2)) < 0)
return get_length(v2);
if (sign(dot(v1, v3)) > 0)
return get_length(v3);
return distance_to_line(p, a, b);
}
Point get_line_projection(Point p, Point a, Point b)
{ // 点在直线上的投影,直线为AB所在直线
Vector v = b - a;
return a + v * (dot(v, p - a) / dot(v, v));
}
bool on_segment(Point p, Point a, Point b)
{ // 点是否在线段上
return sign(cross(p - a, p - b)) == 0 && sign(dot(p - a, p - b)) <= 0;
}
bool segment_intersection(Point a1, Point a2, Point b1, Point b2)
{ // 判断两个线段是否相交
double c1 = cross(a2 - a1, b1 - a1), c2 = cross(a2 - a1, b2 - a1);
double c3 = cross(b2 - b1, a2 - b1), c4 = cross(b2 - b1, a1 - b1);
return sign(c1) * sign(c2) <= 0 && sign(c3) * sign(c4) <= 0;
}
// 多边形
double polygon_area(Point p[], int n)
{ // 求多边形面积
double s = 0;
for (int i = 1; i + 1 < n; i++)
s += cross(p[i] - p[0], p[i + 1] - p[i]);
return s / 2;
}
}
using namespace Geometry;
单调队列
#include<bits/stdc++.h> #define int long long using namespace std; int a[1000010]; int h[1000010]; int hh[1000010]; int l=1,r=0; void solve() { int n,k; cin>>n>>k; for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++) { while(r>=l&&h[r]>a[i])r--; h[++r]=a[i]; hh[r]=i; if(hh[l]+k<=i)l++; if(i>=k)cout<<h[l]<<" "; } cout<<"\n"; l=1,r=0; for(int i=1;i<=n;i++) { while(r>=l&&h[r]<a[i])r--; h[++r]=a[i]; hh[r]=i; if(hh[l]+k<=i)l++; if(i>=k)cout<<h[l]<<" "; } } signed main() { std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); // int t; // cin>>t; // while(t--) solve(); }
字符串哈希
kmp
#include<bits/stdc++.h> #define int long long using namespace std; void solve() { string a; string b; cin>>a>>b; int n=a.size(); int m=b.size(); vector<int>ne(m); for(int i=1,j=0;i<m;i++)// { while(j&&b[j]!=b[i])j=ne[j-1]; if(b[i]==b[j])j++; ne[i]=j; } for(int i=0,j=0;i<n;i++) { while(j&&a[i]!=b[j])j=ne[j-1]; if(a[i]==b[j])j++; if(j==m) { cout<<i-m+2<<"\n"; j=ne[m-1]; } } for(int i=0;i<m;i++) cout<<ne[i]<<" "; } signed main() { std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); // int t; // cin>>t; // while(t--) solve(); }
拓展kmp
#include <bits/stdc++.h> using namespace std; void solve() { string a; string b; cin>>a>>b; int m=b.size(); b+=" "; b+=a; int n=b.size(); vector<int>z1(n); for(int i=1,l=0,r=0;i<n;i++) { if(z1[i-l]<r-i+1) { z1[i]=z1[i-l]; } else { z1[i]=max(0,r-i+1); while(i+z1[i]<n&&b[z1[i]]==b[z1[i]+i])z1[i]++; l=i; r=i+z1[i]-1; } } z1[0]=m; long long ans1=0ll; long long ans2=0ll; for(int i=0;i<m;i++) { ans1^=1ll*(i+1ll)*(z1[i]+1ll); } for(int i=m+1;i<n;i++) { ans2^=1ll*(i-m)*(z1[i]+1ll); } cout<<ans1<<"\n"<<ans2<<"\n"; } signed main() { cin.tie(0), cout.tie(0); // int t = 1; // cin >> t; // while (t--) solve(); return 0; }
字典树
#include<bits/stdc++.h> using namespace std; const int N=200010; namespace trie { int next[N][26],cnt; bool vis[N],exist[N]; void init() { memset(next,0,sizeof(next)); cnt=1; } void insert(const string &s) { int cur=1; for(auto c:s) { if(!next[cur][c-'a']) next[cur][c-'a']=++cnt; cur=next[cur][c-'a']; } exist[cur]=true; } int find(const string &s) { int cur=1; for(auto c:s) { if(!next[cur][c-'a']) return 0; cur=next[cur][c-'a']; } if(exist[cur])return 1; return 0; } } void solve() { int n; cin>>n; for(int i=1;i<=n;i++) { char c; cin>>c; if(c=='I') { string a; cin>>a; trie::insert(a); } else { string a; cin>>a; if(trie::find(a)) cout<<1<<"\n"; else cout<<0<<"\n"; } } } signed main() { std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); // int t; // cin>>t; // while(t--) solve(); }
马拉车
#include<bits/stdc++.h> using namespace std; void solve() { string yuan; cin>>yuan; int n=yuan.size(); string a="~"; for(int i=0;i<n;i++) { a+=yuan[i]; a+="~"; } n=a.size(); vector<int>d(n); for(int i=0,l=0,r=-1;i<n;i++) { int j=l+r-i; int dj=j>=0?d[j]:0; d[i]=max(min(dj,j-l+1),0); if(j-dj<l) { while(i-d[i]>=0&&i+d[i]<n&&a[i-d[i]]==a[i+d[i]])d[i]++; l=i-d[i]+1; r=i+d[i]-1; } } int ans=0; for(int i=1;i<n;i+=2) { ans=max(ans,(d[i]-1)/2*2+1); } for(int i=0;i<n;i+=2) { ans=max(ans,(d[i]-1)/2*2); } cout<<ans<<"\n"; } signed main() { std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); // int t; // cin>>t; // while(t--) solve(); }
分割线——————————————————————————————————————————————————————————————————————————
数学
组合数板子
typedef __int128 Int; typedef pair<int,int> pii; const int mod=1e9+7; const int maxn=1000010; int fect[maxn], infect[maxn]; ll binpow(ll a,ll b,ll c){ ll ans=1; while(b){ if(b&1) ans=(Int)ans*a%c; a=(Int)a*a%c; b>>=1; } return ans; } int C(int a,int b){ return fect[a]*infect[b]%mod*infect[a-b]%mod; } void initzuhe(int n){ fect[0]=1; infect[0]=1; for(int i=1;i<=n;i++){ fect[i]=(fect[i-1]*i)%mod; } infect[n]=binpow(fect[n],mod-2,mod); for(int i=n-1;i>=1;i--) infect[i]=infect[i+1]*(i+1)%mod; }
不取模的组合数
for(int i=0;i<=n;i++){
res[i][0]=res[i][i]=1;
for(int j=1;j<i;j++)
res[i][j]=(res[i-1][j]+res[i-1][j-1])%mod;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号