量化的gpt2模型代码解析

架构图：

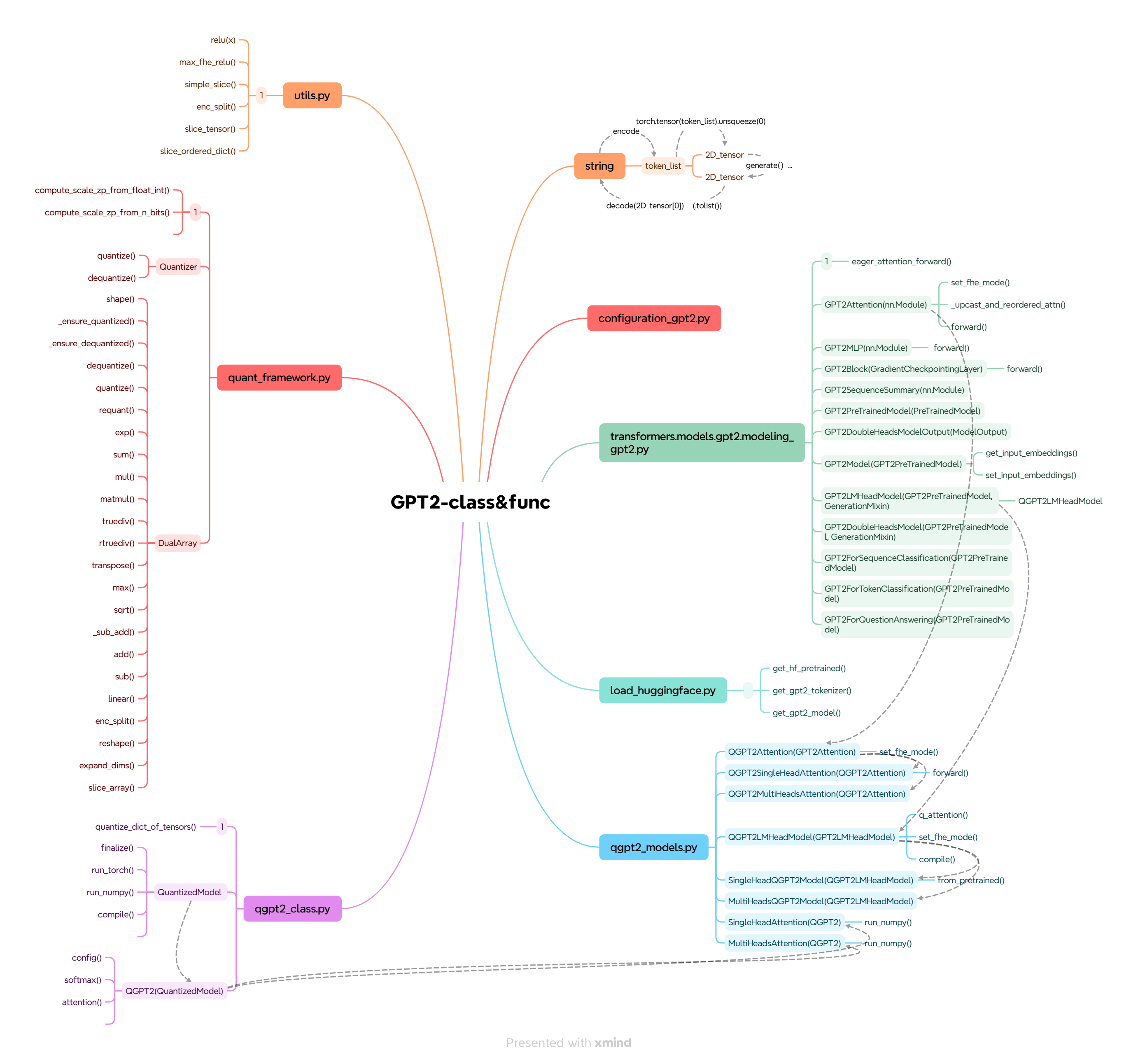
utils.py

from collections import OrderedDict  #保留键值对的插入顺序，处理有序键值对的张量切片。

import numpy as np
import torch

from concrete import fhe

def relu(x):
    """定义ReLU函数。（Rectified Linear Unit，修正线性单元）为神经网络引入非线性，让模型能够学习复杂的非线性关系"""
    return np.maximum(0, x)

该函数是对ReLU（修正线性单元） 这一神经网络核心激活函数的实现，具体解析如下：

1. 函数功能定位：

   作为激活函数，其核心作用是为神经网络引入非线性—— 若没有非线性激活，多层神经网络会退化为单层线性模型，无法学习复杂的数据模式（如图像、文本中的抽象特征）。

2. 核心逻辑与实现：

   • 输入参数 x：通常是神经网络某一层的输出张量（或数组），可能包含正数、零或负数。
   • 计算逻辑：通过np.maximum(0, x)实现 “阈值化”—— 保留所有非负数值（即x ≥ 0时输出x），将所有负数值替换为 0（即x < 0时输出 0）。示例：若x = [-2, 1.5, 0, -0.3]，则relu(x) = [0, 1.5, 0, 0]。

3. 关键特性与意义：

   • 解决 “梯度消失” 问题：相比早期的 sigmoid 函数，ReLU 的梯度在正区间恒为 1（而非趋近于 0），能有效避免深层网络训练时梯度逐层衰减的问题。
   • 计算高效：仅需简单的比较和取值操作，无复杂指数 / 三角函数运算，对硬件友好，适合大规模神经网络。
   • 稀疏激活：会将部分神经元输出置 0，降低网络冗余，间接提升模型泛化能力。

def max_fhe_relu(q_x, axis=-1, keepdims=True):
    """沿指定轴查找FHE中的最大值."""
    with fhe.tag("Max"):
        #规范化轴以处理负值
        axis = axis if axis >= 0 else q_x.ndim + axis

        # 将结果初始化为沿指定轴的第一个切片
        slicer = [slice(None)] * q_x.ndim
        slicer[axis] = 0
        result = q_x[tuple(slicer)]

        # 沿指定轴迭代
        for i in range(1, q_x.shape[axis]):
            slicer[axis] = i
            next_element = q_x[tuple(slicer)]
            result = result + relu(next_element - result)

        # 如果keepdims为True，则保持与输入相同的维度
        if keepdims:
            shape = list(result.shape)
            shape.insert(axis, 1)
            result = result.reshape(shape)

    return result

该函数是面向全同态加密（FHE）场景的最大值计算工具，核心是在加密数据上沿指定维度实现最大值求解，同时兼容 ReLU 函数的非线性特性以适配神经网络需求，以下分核心功能、关键步骤、FHE 适配性三部分解析：

一、核心功能定位

• 场景：用于全同态加密（FHE）环境（通过fhe.tag("Max")标记，关联 FHE 计算流程），解决 “加密数据无法直接解密后求最大值” 的问题。
• 目标：沿输入张量q_x的指定轴（axis）计算最大值，且可选择保留原维度（keepdims），输出结果仍为加密态（或适配 FHE 的量化态）。
• 依赖：结合relu函数（修正线性单元）实现 “比较 - 取大” 的逻辑，避免 FHE 中复杂的分支判断操作。

二、关键步骤拆解（按代码执行顺序）

1. 轴规范化：处理负轴索引

axis = axis if axis >= 0 else q_x.ndim + axis

• 作用：统一轴的索引方式（如输入axis=-1时，自动转换为 “最后一个维度”，q_x.ndim是输入张量的总维度数），避免后续切片出错。
• 示例：若q_x是形状为(3,4,5)的 3 维张量，axis=-1会转为2（最后一维），axis=-2转为1（中间一维）。

2. 初始化结果：取轴上第一个元素

slicer = [slice(None)] * q_x.ndim  # 生成与维度数匹配的“全切片”列表
slicer[axis] = 0                   # 将指定轴的切片设为“第0个元素”
result = q_x[tuple(slicer)]        # 提取指定轴第0个元素，作为初始最大值

• 逻辑：以轴上的第一个元素为 “初始最大值”，后续通过迭代与其他元素比较，逐步更新最大值。
• 示例：若q_x形状(3,4)、axis=1（列维度），slicer会是[slice(None), 0]，即提取所有行的第 0 列元素（形状(3,)）作为初始result。

3. 迭代比较：用 ReLU 实现 “取大” 逻辑

for i in range(1, q_x.shape[axis]):  # 从轴的第1个元素开始迭代（跳过已初始化的第0个）
    slicer[axis] = i                 # 切片指向当前迭代的元素
    next_element = q_x[tuple(slicer)]# 提取当前元素
    result = result + relu(next_element - result)  # 核心：更新最大值

• 核心原理：利用relu函数的特性（relu(x)=max(0,x)），将 “比较大小” 转化为线性计算（适配 FHE 对复杂逻辑的限制）：
  • 若next_element > result：next_element - result > 0，relu(...)输出差值，result + 差值 = next_element（更新为更大值）；
  • 若next_element ≤ result：next_element - result ≤ 0，relu(...)输出 0，result + 0 = result（保持原最大值不变）。
• 优势：避免 FHE 中难以实现的if-else分支判断，用 “加法 + ReLU” 的简单操作完成比较，降低加密计算复杂度。

4. 维度保持：按需保留原维度结构

if keepdims:
    shape = list(result.shape)
    shape.insert(axis, 1)  # 在指定轴位置插入“1”维度
    result = result.reshape(shape)

• 作用：确保输出张量的维度与输入兼容（尤其在神经网络层连接中，避免维度不匹配）。
• 示例：若输入q_x形状(3,4)、axis=1，未启用keepdims时result形状为(3,)；启用后会插入维度1，形状变为(3,1)，与输入的 “行维度” 保持一致。

三、FHE 适配性设计

1. 无分支计算：通过relu将比较逻辑转化为 “加法 + 非线性激活”，避免 FHE 中效率极低的条件判断（FHE 对线性操作支持更友好，分支会大幅增加计算开销）。
2. fhe.tag("Max")标记：为 FHE 编译器提供 “该模块是最大值计算” 的元信息，帮助编译器优化加密计算流程（如选择合适的加密参数、减少噪声积累）。
3. 切片操作可控：仅使用简单的slice切片（而非高级索引），确保加密张量的索引操作可被 FHE 框架高效支持，避免因复杂索引导致的加密状态异常。

def simple_slice(array, indices, axis):
    # 这与np.take()的作用相同，只是仅支持简单切片，不支持高级索引，因此速度快得多
    sl = [slice(None)] * array.ndim
    sl[axis] = indices
    return array[tuple(sl)]

该函数是一个简化版的数组切片工具，核心作用是按指定维度和索引规则提取数组元素，本质是对 NumPy/PyTorch 等数组的切片逻辑做了封装，以下从核心逻辑、参数含义、功能特点三方面简要解析：

1. 核心逻辑（3 步）

函数通过构建「全维度切片规则」，仅在目标维度替换为自定义索引，最终实现精准切片，步骤如下：

• 步骤 1：初始化全维度 “默认切片”

  sl = [slice(None)] * array.ndim

  slice(None) 等价于切片中的 :（表示 “取该维度所有元素”），这里根据数组的维度数（array.ndim），生成一个 “全取所有维度” 的切片列表。

  例：若数组是 2 维（ndim=2），则 sl 初始为 [slice(None), slice(None)]，对应切片 [:, :]。

• 步骤 2：替换目标维度的切片规则

  sl[axis] = indices

  将 “全取列表” 中「目标维度（axis）」的规则，替换为用户指定的索引（indices），其他维度仍保持 “全取”。

  例：数组 2 维，axis=0、indices=slice(1,3)（即取第 1-2 行，左闭右开），则 sl 变为 [slice(1,3), slice(None)]，对应切片 [1:3, :]。

• 步骤 3：执行切片并返回结果

  return array[tuple(sl)]

  将切片列表（sl）转为元组（数组切片需元组格式），传入数组实现切片，最终返回切片后的结果。

2. 关键参数含义

参数	作用
array	待切片的数组（支持 NumPy 数组、PyTorch 张量等支持切片语法的数据结构）
indices	目标维度的索引规则（仅支持 “简单切片”，如 slice(1,5)、2，不支持列表 / 数组等高级索引）
axis	要切片的目标维度（整数，如 0 表示行、1 表示列，需符合数组维度范围）

3. 功能特点（与 np.take() 对比）

• 相同点：核心目的一致 —— 按指定维度提取元素，避免手动写复杂切片。

• 不同点

  ：

  • 支持索引类型：仅支持「简单切片」（: 或单个整数），不支持 np.take() 能处理的列表、数组等 “高级索引”；
  • 速度：因舍弃了高级索引的复杂逻辑，仅保留基础切片功能，所以执行速度更快（适合对性能敏感、仅需简单切片的场景，如加密计算（代码中关联 FHE）的轻量化切片需求）。

示例（以 NumPy 数组为例）

import numpy as np

arr = np.array([[1,2,3], [4,5,6], [7,8,9]])  # 2维数组（ndim=2）

# 需求：取第0维度（行）的第1-2行（索引1、2），第1维度（列）全取
result = simple_slice(array=arr, indices=slice(1,3), axis=0)
# 等价于 arr[1:3, :]，结果为：[[4,5,6], [7,8,9]]

# 需求：取第1维度（列）的第0列（索引0），第0维度（行）全取
result2 = simple_slice(array=arr, indices=0, axis=1)
# 等价于 arr[:, 0]，结果为：[1,4,7]

def enc_split(array, n, axis):
    n_total = array.shape[axis]

    assert (
        n_total % n == 0
    ), f"array of shape {array.shape} cannot be split into {n} sub-arrays along axis {axis}"

    section = n_total // n

    split_arrays = ()
    for i in range(n):
        split_array = simple_slice(
            array=array, indices=slice(i * section, (i + 1) * section), axis=axis
        )
        split_arrays += (split_array,)

    return split_arrays

该函数 enc_split 的核心作用是将输入数组（如张量）沿指定维度 axis 均匀分割成 n 个等长的子数组，是面向加密计算（从命名 enc_ 推测）场景的数组分割工具，具体解析如下：

1. 函数参数说明

参数名	类型	作用
array	数组 / 张量	待分割的原始数据（如 numpy 数组、FHE 加密张量等，需支持 shape 属性和切片）
n	整数	要分割成的子数组数量
axis	整数	执行分割的维度（如 axis=0 表示沿行分割，axis=1 表示沿列分割）

2. 核心逻辑拆解（分 4 步）

步骤 1：获取目标维度的总长度

n_total = array.shape[axis]

通过 array.shape[axis] 拿到原始数组在 axis 维度上的总元素个数（比如数组 shape 为 (10, 5)，axis=0 时 n_total=10）。

步骤 2：校验分割可行性（关键断言）

assert (n_total % n == 0), f"array of shape {array.shape} cannot be split into {n} sub-arrays along axis {axis}"

• 核心判断：n_total % n == 0，即目标维度的总长度必须能被 n 整除（保证分割后每个子数组长度相等）；
• 报错提示：若不满足整除（如 n_total=10、n=3），则抛出断言错误，明确告知原始数组形状、目标分割数和维度，便于排查问题。

步骤 3：计算每个子数组的长度

section = n_total // n

section 是分割后每个子数组在 axis 维度上的长度（如 n_total=10、n=2 时，section=5，即每个子数组沿 axis=0 占 5 个元素）。

步骤 4：循环切片，生成子数组 tuple

split_arrays = ()  # 初始化空元组，用于存储子数组
for i in range(n):
    # 计算当前子数组的切片范围：[i*section, (i+1)*section)
    split_array = simple_slice(array=array, indices=slice(i * section, (i + 1) * section), axis=axis)
    split_arrays += (split_array,)  # 将当前子数组加入元组
return split_arrays

• 循环 n 次（对应 n 个子数组），每次通过 simple_slice 函数（自定义的轻量切片工具，比 np.take 快）截取当前子数组；
• 切片范围 slice(i*section, (i+1)*section) 确保每个子数组在 axis 维度上不重叠、全覆盖（如 i=0 时取 [0,section)，i=1 时取 [section,2*section) 等）；
• 最终返回存储所有子数组的元组（元组不可变，适合存储固定数量的分割结果）。

3. 关键特性与适用场景

• 强约束性：仅支持 “均匀分割”（子数组长度必须相等），非均匀分割会直接报错，避免后续计算中因子数组长度不一致导致的问题；
• 轻量高效：依赖自定义的 simple_slice 而非 numpy 高级索引，减少计算开销，适合对性能敏感的场景（如加密张量处理，enc_ 命名暗示此用途）；
• 维度兼容：支持任意合法维度（只要 axis 在数组维度范围内），灵活性较高。

4. 示例（帮助理解）

假设输入：

• array 是 shape 为 (8, 3) 的 numpy 数组（8 行 3 列）；
• n=4（分割成 4 个子数组）；
• axis=0（沿行分割）。

执行过程：

1. n_total = 8（axis=0 维度总长度）；
2. 校验 8%4==0（满足，不报错）；
3. section=8//4=2（每个子数组沿行占 2 个元素）；
4. 循环 4 次：
   • i=0：切片 [0,2) → 子数组 shape (2,3)；
   • i=1：切片 [2,4) → 子数组 shape (2,3)；
   • i=2：切片 [4,6) → 子数组 shape (2,3)；
   • i=3：切片 [6,8) → 子数组 shape (2,3)；
5. 返回包含 4 个 (2,3) 数组的元组。

def slice_tensor(tensor, dim=0, indices=None):
    if tensor is None or indices is None:
        return tensor

    if isinstance(indices, int):
        sliced_tensor = tensor.select(dim, indices)
    else:
        sliced_tensor = tensor.index_select(dim, torch.tensor(indices).flatten())

    return sliced_tensor

该函数是基于 PyTorch 的张量切片工具函数，核心作用是按指定维度和索引，从输入张量中提取部分数据，逻辑清晰且适配不同索引类型，以下是分模块解析：

1. 函数基本信息

• 功能定位：对 PyTorch 张量（tensor）进行维度切片，支持单个索引或多个索引的提取需求。

• 参数说明

  ：

  • tensor：输入的 PyTorch 张量（核心操作对象，若为None则直接返回）；
  • dim=0：指定切片的维度（默认对第 0 维切片，如对形状(3,4,5)的张量，dim=1表示沿 “列” 方向切片）；
  • indices=None：指定要提取的索引（可为单个整数或索引列表 / 数组，若为None则直接返回原张量）。

2. 核心逻辑分支

（1）边界条件处理

if tensor is None or indices is None:
    return tensor

• 若输入张量本身为空（None），或未指定要提取的索引（indices=None），则不做任何操作，直接返回原输入 —— 避免无效计算或报错。

（2）单个索引的切片（indices为整数）

if isinstance(indices, int):
    sliced_tensor = tensor.select(dim, indices)

• 当indices是单个整数时（如indices=2），调用 PyTorch 原生方法torch.Tensor.select(dim, index)：
  • 作用：在指定维度（dim）上，提取单个位置的切片，并降低一个维度（如对(3,4,5)的张量，dim=0, indices=1后，输出形状变为(4,5)）；
  • 示例：tensor = torch.tensor([[1,2],[3,4],[5,6]])，slice_tensor(tensor, dim=0, indices=1) → 输出tensor([3,4])。

（3）多个索引的切片（indices为非整数）

else:
    sliced_tensor = tensor.index_select(dim, torch.tensor(indices).flatten())

• 当indices是列表、数组等非整数类型时（如indices=[0,2]），分两步操作：

  1. torch.tensor(indices).flatten()：先将输入的索引转换为 PyTorch 张量，并通过flatten()确保索引是一维的（避免多维索引导致的维度混乱）；
  2. tensor.index_select(dim, ...)：调用 PyTorch 原生方法torch.Tensor.index_select()，在指定维度上提取多个位置的切片，保持原维度数不变（仅改变指定维度的长度）；
  • 示例：tensor = torch.tensor([[1,2],[3,4],[5,6]])，slice_tensor(tensor, dim=0, indices=[0,2]) → 输出tensor([[1,2],[5,6]])（形状仍为(2,2)，仅第 0 维长度从 3 变为 2）。

3. 函数返回值

最终返回切片后的新张量（sliced_tensor），原输入张量不会被修改（PyTorch 张量操作默认返回新对象，不改变原张量）。

总结

该函数是对 PyTorch 原生切片方法（select/index_select）的封装优化：

• 简化了使用：统一了 “单个索引” 和 “多个索引” 的调用方式，无需用户手动区分两种方法；
• 增强了鲁棒性：处理了None输入的边界情况，避免报错；
• 适配性强：支持列表、数组等多种索引格式，且通过flatten()确保索引有效性，适合在神经网络数据处理（如特征筛选、样本提取）中复用。

def slice_ordered_dict(odict, dim=0, indices=None):
    return OrderedDict((k, slice_tensor(v, dim=dim, indices=indices)) for k, v in odict.items())

要解析 slice_ordered_dict 函数，需结合其依赖的 OrderedDict（有序字典）和 slice_tensor 函数，从功能定位、参数含义、执行逻辑、核心作用四个维度拆解：

1. 核心功能定位

这是一个针对 “有序字典” 的张量切片工具函数—— 当有序字典（odict）的 “值” 都是 PyTorch 张量时，该函数会对字典中每个键对应的张量，按相同规则进行切片操作，并返回保持原键值对顺序的新有序字典。

2. 参数含义

参数名	类型	作用	默认值
odict	OrderedDict	输入的有序字典，要求其所有值都是 PyTorch 张量（键可任意，仅用于保留映射关系）	-（必传）
dim	int	对张量进行切片的 “维度”（例如 dim=0 表示沿张量的第 0 维切片，对应样本维度）	0
indices	int / 整数序列	切片的 “索引位置”：- 若为 int：取张量在 dim 维度上该索引对应的单个元素；- 若为序列（如 [1,3,5]）：取张量在 dim 维度上这些索引对应的多个元素；- 若为 None：不切片，直接返回原张量	None

3. 执行逻辑（分步拆解）

函数本质是遍历有序字典 + 调用 slice_tensor 处理每个张量 + 重建有序字典，步骤如下：

1. 遍历键值对：通过 odict.items() 遍历输入有序字典的每一组 (键 k, 值 v)（v 是 PyTorch 张量）；
2. 张量切片：对每个张量 v，调用 slice_tensor(v, dim=dim, indices=indices)，按指定维度和索引完成切片（slice_tensor 的逻辑已在代码中定义：处理 int/ 序列索引，返回切片后的张量）；
3. 重建有序字典：将 “原键 k + 切片后的张量” 作为新键值对，传入 OrderedDict 构造器，生成并返回保持原键值对顺序的新有序字典（这是 OrderedDict 相比普通字典的核心特性）。

4. 典型使用场景

常用于深度学习中对 “多张量有序集合” 的批量切片，例如：

• 当 odict 存储 “模型输入的多特征张量”（如 {"image": 图像张量, "label": 标签张量}），需沿 dim=0（样本维度）截取部分样本时，调用该函数可一次性完成所有张量的切片，且保证 “图像 - 标签” 的样本对应关系不打乱；
• 当 odict 存储 “多输出层的预测张量”，需按维度提取特定通道 / 特征时，避免逐个处理字典值，提升代码简洁性。

quant_framework.py

from __future__ import annotations  #延迟类型注解解析

from typing import List, Optional, Tuple, Union  #类型提示工具

import numpy as np
from concrete.fhe.tracing import Tracer
from utils import enc_split, max_fhe_relu, simple_slice  #自定义 ：加密数据分割、适配激活函数、数组切片简化

EPSILON = 2**-11  #微小偏移量，避免除零错误、量化过程中的精度丢失。

import numpy as np

def compute_scale_zp_from_float_int(
    float_array: np.ndarray, int_array: np.ndarray, is_symmetric: bool = True
) -> Tuple[float, Union[float, int]]:
    """根据浮点数及其相关的量化值计算缩放因子和零点。
    参数：
        float_array（np.ndarray）：浮点数值。
        int_array（np.ndarray）：与浮点数值相关联的量化值。
        is_symmetric（bool）：量化是否应为对称的。默认为True。
    返回：
        （scale，zp）（Tuple[float, Union[float, int]]）：值的缩放因子和零点。
    """

    # 获取输入的最小值和最大值
    float_array_min, float_array_max = np.min(float_array), np.max(float_array)
    int_array_min, int_array_max = np.min(int_array), np.max(int_array)

    # 如果量化值的最小值和最大值相同，则缩放因子为1，零点为0
    if int_array_min == int_array_max:
        scale = 1
        zp = 0

    else:
        # 在对称量化中，零点被设为0
        if is_symmetric:
            scale = (float_array_max - float_array_min) / (int_array_max - int_array_min)
            zp = 0

        else:
            scale = (float_array_max - float_array_min) / (int_array_max - int_array_min)
            zp = (-float_array_max * int_array_min + float_array_min * int_array_max) / (
                float_array_min - float_array_max
            )

    return scale, zp

该函数是数值量化场景中的核心工具，用于根据 “原始浮点数数组” 和其对应的 “量化后整数数组”，计算两者之间的映射关系（缩放因子scale和零点zp），实现浮点数与整数的精准转换，常见于机器学习模型量化（如模型压缩、边缘设备部署）或加密计算中。

1. 核心功能与参数解析

要素	说明
函数作用	建立 “浮点数（连续值）” 与 “整数（离散量化值）” 的映射规则，输出scale（缩放）和zp（零点）
输入参数	- float_array：原始未量化的浮点数数组（如模型权重、输入特征）- int_array：与浮点数一一对应的量化后整数数组（如 8bit/16bit 整数）- is_symmetric：是否启用对称量化（默认True，量化范围关于 0 对称，如 - 127~127；False为非对称量化，如 0~255）
返回值	- scale：缩放因子（浮点数→整数需乘scale，整数→浮点数需除scale）- zp：零点（量化映射的偏移量，对称量化中固定为 0）

2. 核心逻辑分步拆解

函数通过 “先判断特殊情况，再分量化模式计算” 的逻辑执行：

步骤 1：获取极值，确定数值范围

先分别计算浮点数数组和整数数组的最小值、最大值，为后续映射计算提供范围依据：

float_array_min, float_array_max = np.min(float_array), np.max(float_array)  # 浮点数的数值区间
int_array_min, int_array_max = np.min(int_array), np.max(int_array)          # 量化整数的数值区间

步骤 2：处理特殊情况（整数数组无变化）

若量化后的整数数组所有值相同（int_array_min == int_array_max），说明浮点数未被有效量化（或所有值映射到同一个整数），此时无需缩放和偏移，直接返回默认值：

• scale=1（无缩放）
• zp=0（无偏移）

步骤 3：分量化模式计算scale和zp

当整数数组有有效范围（int_array_min != int_array_max）时，分两种模式计算：

模式 A：对称量化（is_symmetric=True，默认）

• 核心特点：量化后的整数范围关于 0 对称（如 - 63_63、-127127），因此zp=0（无偏移）。

• scale计算

  ：用浮点数的数值跨度，除以整数的数值跨度，得到 “1 个整数单位对应多少浮点数单位”：

  scale = (浮点数最大值 - 浮点数最小值) / (整数最大值 - 整数最小值)
  

  例：浮点数范围[-1.2, 1.2]，整数范围[-120, 120]，则scale=(1.2 - (-1.2))/(120 - (-120))=2.4/240=0.01（1 个整数单位对应 0.01 浮点数单位）。

模式 B：非对称量化（is_symmetric=False）

• 核心特点：量化后的整数范围不关于 0 对称（如 0~255），因此zp不为 0（需通过偏移量适配浮点数与整数的范围）。

• scale计算：与对称量化一致（因scale仅反映 “数值跨度的比例”，与是否对称无关）。

• zp计算

  ：通过线性方程推导，找到 “浮点数 0 对应的整数位置”，公式本质是求解浮点数与整数的线性映射偏移：

  zp = (-float_max * int_min + float_min * int_max) / (float_min - float_max)
  

  例：浮点数范围[0.1, 0.3]，整数范围[10, 30]，则zp=(-0.310 + 0.130)/(0.1-0.3)=(-3+3)/(-0.2)=0（此例特殊，实际非对称场景zp通常非 0）。

3. 关键意义

量化的本质是 “用更少的存储空间 / 计算资源表示数值”，而该函数输出的scale和zp是量化 / 反量化的 “钥匙”：

• 量化（浮点数→整数）：int_val = round(float_val / scale + zp)
• 反量化（整数→浮点数）：float_val = (int_val - zp) * scale

通过这两个参数，可在 “精度损失可控” 的前提下，实现数值的压缩与恢复，是模型部署、低资源设备计算的基础工具。

def compute_scale_zp_from_n_bits(
    float_array: np.ndarray, n_bits: int, is_symmetric: bool = True
) -> Tuple[float, Union[float, int]]:
    """基于浮点数和用于量化的位数计算缩放因子和零点。
    参数：
        float_array（np.ndarray）：浮点数值。
        n_bits（int）：用于量化浮点数的位数。
        is_symmetric（bool）：量化是否应为对称的。默认为True。
    返回：
        （scale，zp）（Tuple[float, Union[float, int]]）：值的缩放因子和零点。
    """

    if not is_symmetric:
        raise NotImplementedError("is_symmetric = False is not yet fully supported.")

    # 获取输入的最小值和最大值
    min_val = np.min(float_array)
    max_val = np.max(float_array)

    # 如果这些值的最小值和最大值相同，那么缩放因子为1，零点为0
    if min_val == max_val:
        scale = 1
        zero_point = 0

    # 否则，对n_bits应用对称量化
    else:
        max_abs_val = np.maximum(abs(min_val), abs(max_val))
        scale = max_abs_val / (2 ** (n_bits - 1) - 1)
        zero_point = 0

    return scale, zero_point

该函数是神经网络模型量化场景中的核心工具，用于根据输入浮点数数组和目标量化位数，计算将浮点数映射为整数（量化值）所需的关键参数 ——缩放因子（scale） 和零点（zero_point），核心逻辑围绕 “对称量化” 展开，具体解析如下：

1. 核心功能定位

量化的本质是将高精度浮点数（如 32 位 float）转换为低精度整数（如 8 位 int），以降低模型存储和计算成本。该函数通过计算scale和zero_point，定义了 “浮点数→整数” 的映射规则（对称模式下），是量化过程的基础。

2. 关键参数与返回值

类别	名称 / 参数	作用说明
输入参数	float_array	待量化的原始浮点数数组（如模型权重、激活值），用 numpy 数组存储。
输入参数	n_bits	目标量化位数（如 8、16），决定量化后整数的取值范围（对称量化下有固定规则）。
输入参数	is_symmetric	量化模式开关，当前仅支持True（对称量化），False（非对称）暂未实现。
返回值	scale（缩放因子）	浮点数与量化整数的 “比例系数”，用于将浮点数缩放到整数范围。
返回值	zero_point（零点）	量化后与 “浮点数 0” 对应的整数（对称量化下固定为 0），保证映射的偏移正确性。

3. 核心逻辑拆解（分场景）

函数按输入浮点数的分布特点，分两种场景计算参数：

场景 1：输入浮点数全为同一个值（min_val == max_val）

• 此时浮点数无需缩放（所有值相同，量化后也为同一个整数），因此：
  • scale = 1（缩放比例为 1，浮点数直接对应整数）；
  • zero_point = 0（对称量化的默认零点）。

场景 2：输入浮点数有取值范围（min_val != max_val）

• 第一步：计算 “绝对最大值”max_abs_val

  取浮点数数组中 “最小值的绝对值” 和 “最大值的绝对值” 中的较大者（如数组[-5, 3]，max_abs_val = max(5,3) =5），确保覆盖所有浮点数的取值范围。

• 第二步：计算scale（核心公式）

  公式：scale = max_abs_val / (2^(n_bits -1) - 1)

  • 分母2^(n_bits-1) -1：是对称量化下整数的最大取值（如 8 位量化：2^(8-1)-1 = 127，即整数范围为[-127, 127]）；
  • 含义：将浮点数的 “最大绝对范围”（max_abs_val）均匀映射到整数的 “最大取值范围”，确保浮点数缩放后能被整数精准表示。

• 第三步：固定zero_point = 0

  对称量化的核心特征 —— 量化后的整数范围关于 0 对称（如[-127,127]），因此 “浮点数 0” 对应 “整数 0”，零点固定为 0。

4. 典型示例（帮助理解）

假设输入：

• float_array = [-4.0, 2.0, -3.5, 1.8]（min_val=-4.0，max_val=2.0）；
• n_bits=8（目标 8 位对称量化）。

计算过程：

1. max_abs_val = max(abs(-4.0), abs(2.0)) =4.0；
2. scale = 4.0 / (2^(8-1)-1) =4.0 /127 ≈0.031496；
3. zero_point=0。

最终量化映射规则：

量化整数 = round (浮点数 /scale) + zero_point

（如浮点数-4.0 → -4.0 /0.031496 ≈-127，对应 8 位整数-127；浮点数2.0 → 2.0/0.031496≈63，对应整数63）。

class Quantizer:

提供用于处理任何量化算子的方法的量化器类。

def __init__(self, n_bits: int = 8):
        """使用量化中要用到的位数进行初始化。
        量化器实例主要用于在字典中存储所有的缩放因子和零点。
        这些量化参数中的每一个都通过其唯一键与特定的量化算子相关联。为了计算并存储它们，首先会使用输入集以浮点形式进行一次校准。然后，在全同态加密（FHE）计算过程中，这些参数会被重新使用，以正确地对数值进行量化和反量化。
        参数：
            n_bits（int）：用于量化的位数。
        """
        self.n_bits = n_bits
        self.scale_dict = {}

这是一个量化器类的构造方法（__init__），核心作用是初始化量化所需的基础配置，并创建存储量化关键参数的容器，为后续 “校准计算量化参数” 和 “FHE 过程中复用参数” 做准备。具体解析如下：

1. 方法核心定位

• 属于 “量化器” 类的初始化逻辑，在创建量化器实例时自动执行。
• 核心目标：确定量化精度（位数）+ 搭建量化参数的存储结构，为后续全同态加密（FHE）场景下的 “量化 / 反量化” 操作铺路。

2. 关键参数与属性解析

元素	类型	作用说明
n_bits: int = 8	入参（默认值 8）	定义 “量化精度”：用多少位整数来近似表示原本的浮点数（如 8 位、16 位），默认 8 位是常用的平衡精度与计算成本的选择。
self.n_bits	实例属性	将入参的量化位数 “保存到实例中”，后续计算量化参数（如缩放因子）时会复用这个精度配置。
self.scale_dict = {}	实例属性（空字典）	用于存储量化关键参数（缩放因子） 的容器：- 键（key）：对应 “特定量化算子” 的唯一标识（比如不同层的卷积 / 激活算子）；- 值（value）：该算子对应的 “缩放因子”（量化时浮点数→整数的核心转换系数）；- 后续通过 “校准过程” 计算出各算子的缩放因子后，会存入这个字典，供 FHE 计算时调用。

3. 背后的业务逻辑关联（结合注释补充）

构造方法的设计，是为了衔接后续两个关键流程：

1. 第一步：校准阶段（浮点输入）

   后续会用 “浮点形式的输入集” 跑一次校准，根据 self.n_bits 定义的精度，计算出每个量化算子对应的 “缩放因子”（可能还有零点，此处字典暂存缩放因子），并把这些参数存入 self.scale_dict。

2. 第二步：FHE 计算阶段

   FHE 计算中无法直接处理浮点数，需先将浮点数按 self.scale_dict 中的参数 “量化” 为整数（浮点数 ÷ 缩放因子 → 整数），计算完成后再 “反量化” 回浮点数（整数 × 缩放因子 → 原始精度浮点数）—— 而 self.n_bits 和 self.scale_dict 就是这两步转换的核心依据。

总结

这个构造方法本质是 “量化器的初始化脚手架”：通过 self.n_bits 固定量化精度，通过 self.scale_dict 预留参数存储位置，确保后续校准和 FHE 计算时，量化过程有统一的配置和可复用的参数，最终实现 “浮点数→整数（FHE 计算）→浮点数” 的正确转换。

def quantize(
        self, float_array: np.ndarray, key: Optional[str] = None, is_symmetric: bool = True
    ) -> np.ndarray:
        """对浮点数组进行量化。
        参数：
            float_array（np.ndarray）：浮点数值。
            key（Optional[str]）：如果已知float_array的缩放因子和零点，则该键用于表示它们。如果为None，则浮点数将基于n_bits进行量化。默认为None。
            is_symmetric（bool）：量化是否应为对称的。默认为True。
        返回：
            np.ndarray：量化后的值。
        """

        # 获取或计算缩放因子和零点
        scale_zp = (
            self.scale_dict[key]
            if key in self.scale_dict
            else compute_scale_zp_from_n_bits(float_array, self.n_bits, is_symmetric)
        )
        self.scale_dict[key] = scale_zp

        # 对这些值进行量化
        return np.rint((float_array / scale_zp[0]) + scale_zp[1]).astype(np.int64)

该 quantize 方法是浮点数组量化的核心函数，作用是将连续的浮点数值映射到离散的整数（量化值），核心逻辑围绕 “获取缩放因子 / 零点” 和 “执行量化计算” 两步展开，以下是分模块解析：

1. 核心功能定位

量化是机器学习（尤其边缘设备、隐私计算如 FHE）中常用的技术，目的是降低数据存储 / 计算成本（整数运算比浮点快、占用内存少）。该函数通过 “缩放 + 偏移” 将浮点数转换为整数，同时支持 “复用已有量化参数” 和 “动态计算参数” 两种模式。

2. 关键参数解读

参数名	类型	作用
float_array	np.ndarray	待量化的原始浮点数组（如模型权重、输入特征）
key	Optional[str]	量化参数（缩放因子 + 零点）的 “索引键”：- 若不为None，优先复用已存储的参数；- 若为None，则基于位数动态计算参数。
is_symmetric	bool	是否启用对称量化（对称量化零点固定为 0，计算更简单；非对称需额外算偏移），默认启用。

3. 核心逻辑拆解（分 2 步）

第一步：获取 / 计算量化核心参数（scale + zp）

量化的本质是通过 “缩放因子（scale）” 和 “零点（zp，zero point）” 建立浮点数与整数的映射关系，公式可简化为：

量化值 = (浮点数 / scale) + zp（逆量化则是 浮点数 ≈ 量化值 * scale - zp）。

该步骤分两种场景处理参数：

1. 场景 1：复用已有参数（key 存在时）
   • 若 key 在类的 scale_dict（一个存储 “key - 量化参数” 的字典）中，直接读取该 key 对应的 (scale, zp)（避免重复计算，适合同一类数据多次量化，如模型同一层的输入）。
2. 场景 2：动态计算参数（key 不存在 / 为 None 时）
   • 调用前文提到的 compute_scale_zp_from_n_bits 函数，基于 float_array 的实际数值范围和预设的 self.n_bits（量化位数，如 8bit、16bit），计算出适配的 (scale, zp)。
3. 参数缓存：无论哪种场景，最终得到的 (scale, zp) 都会存入 scale_dict[key]，供后续同一 key 的数据复用。

第二步：执行量化计算（生成整数数组）

通过以下公式将浮点数转换为整数，核心是 “归一化→偏移→取整→类型转换”：

np.rint((float_array / scale_zp[0]) + scale_zp[1]).astype(np.int64)

逐操作解析：

• float_array / scale_zp[0]：用缩放因子将浮点数 “归一化” 到接近整数的范围（消除数值量级差异）；
• + scale_zp[1]：加上零点（zp），补偿非对称量化的偏移（对称量化时 zp=0，此步无影响）；
• np.rint(...)：对结果四舍五入（确保映射到最近的整数，减少量化误差）；
• .astype(np.int64)：将结果转换为 64 位整数类型（保证数值范围足够，避免溢出）。

4. 典型场景示例（帮助理解）

假设 self.n_bits=8（8bit 对称量化），float_array = np.array([-2.0, 1.5, 3.0])，key=None：

1. 计算 scale：8bit 对称量化的整数范围是 [-127, 127]，float_array 的最大绝对值是 3.0，由 compute_scale_zp_from_n_bits 得 scale=3.0/(2^(8-1)-1)=3/127≈0.0236，zp=0；
2. 量化计算：(float_array / 0.0236) + 0 → 约 [-84.7, 63.6, 127.1]，四舍五入后为 [-85, 64, 127]，最终返回 np.int64 类型数组。

5. 关键注意点

• 对称量化特性：当 is_symmetric=True 时，zp=0，公式简化为 量化值 = np.rint(float_array / scale)，计算效率更高；
• 误差来源：量化误差主要来自 “四舍五入” 和 “scale 映射”，n_bits 越大（如 16bit），误差越小，但存储 / 计算成本越高；
• 参数复用：scale_dict 的设计是核心优化 —— 同一类数据（如模型同一输入层）只需首次计算 scale/zp，后续直接复用，减少重复计算开销。

def dequantize(
        self,
        int_array: np.ndarray,
        float_array: Optional[np.ndarray] = None,
        key: Optional[str] = None,
        is_symmetric: bool = True,
    ) -> np.ndarray:
        """对整数数组进行反量化。
        参数：
            int_array（np.ndarray）：量化后的值。
            float_array（可选[np.ndarray]）：与量化值相关联的浮点值。默认为None。
            key（可选[str]）：如果已知float_array的缩放因子（scale）和零点（zero_point），则该键用于表示它们。如果为None，则使用整数数组和相关联的浮点数组计算缩放因子和零点。默认为None。
            is_symmetric（bool）：量化是否为对称的。默认为True。
        返回：
            np.ndarray：反量化后的值。
        抛出：
            ValueError：如果不存在与输入值相关联的缩放因子和零点，且未提供整数数组或浮点数组中的一个。
        """
        if key not in self.scale_dict and (float_array is None or int_array is None):
            raise ValueError("'float_array' and 'int_array' must be provided.")

        # 如果该键尚不存在，则使用整数数组和浮点数组计算缩放因子和零点数组
        elif key not in self.scale_dict:
            self.scale_dict[key] = compute_scale_zp_from_float_int(
                float_array=float_array, int_array=int_array, is_symmetric=is_symmetric
            )

        # 对这些值进行反量化
        return (int_array - self.scale_dict[key][1]) * self.scale_dict[key][0]

该函数是量化操作的逆过程（反量化），核心是将之前量化得到的整数数组（int_array）还原为接近原始的浮点数组，核心逻辑围绕 “获取缩放因子（scale）和零点（zero_point）→ 执行反量化计算” 展开，以下是分模块解析：

1. 核心功能定位

量化的本质是 “用整数近似表示浮点数”（减少存储 / 计算成本），反量化则是通过量化时的关键参数（scale和zero_point），将整数还原回浮点数。

该函数通过维护self.scale_dict（类实例的字典，存储不同key对应的(scale, zero_point)），避免重复计算关键参数，提升效率。

2. 关键参数解读

参数名	作用
int_array	输入的量化后整数数组（必须提供，是反量化的核心输入）
float_array	可选，与int_array对应的原始 / 参考浮点数数组（用于计算scale和zp）
key	可选，标识scale和zp的 “键”（若已存在于scale_dict，直接复用参数）
is_symmetric	标识量化是否为 “对称量化”（对称量化时zp=0，简化计算，默认启用）

3. 核心逻辑拆解（分 3 步）

步骤 1：参数合法性校验

首先判断 “是否能获取scale和zero_point”，若无法获取则抛错：

if key not in self.scale_dict and (float_array is None or int_array is None):
    raise ValueError("'float_array' and 'int_array' must be provided.")

• 场景：若key不在scale_dict（无缓存的参数），且float_array或int_array有一个缺失 → 无法计算scale和zp，必须抛错要求补充输入。

步骤 2：缓存scale和zero_point（避免重复计算）

若key不在scale_dict（无缓存），但float_array和int_array都存在 → 调用之前定义的compute_scale_zp_from_float_int函数，计算当前key对应的(scale, zp)，并存入scale_dict：

self.scale_dict[key] = compute_scale_zp_from_float_int(...)

• 目的：后续若同一key再次反量化，直接从scale_dict取参数，无需重复计算（提升效率）。

步骤 3：执行反量化计算（核心公式）

反量化的核心公式为：

return (int_array - self.scale_dict[key][1]) * self.scale_dict[key][0]

• 拆解：
  • self.scale_dict[key][1]：当前key对应的零点（zero_point）（量化时用于将浮点数偏移到整数范围）；
  • self.scale_dict[key][0]：当前key对应的缩放因子（scale）（量化时用于将浮点数 “压缩” 到整数范围，反量化时 “还原”）；
  • 逻辑：先通过int_array - zp抵消量化时的偏移，再乘以scale恢复原始数值范围。

4. 典型场景举例

假设某场景下：

• 原始浮点数数组float_array = [1.0, 2.0, 3.0]，量化后整数数组int_array = [10, 20, 30]；
• 调用compute_scale_zp_from_float_int计算得scale=0.1，zp=0（对称量化，zp=0）；
• 反量化计算：(int_array - 0) * 0.1 = [1.0, 2.0, 3.0] → 完美还原原始浮点数。

5. 关键注意点

• 参数复用逻辑：scale_dict是类实例的字典，同一key的参数只会计算一次，适合多次反量化同一来源的int_array；
• 对称量化特性：若is_symmetric=True，zp=0，公式可简化为int_array * scale（减少一次减法运算）；
• 异常边界：仅当 “无缓存参数且缺少float_array/int_array” 时抛错，确保反量化始终有合法的scale和zp。

class DualArray

一种双重表示数组，同时传播浮点数及其量化版本

def __init__(
        self,
        float_array: Optional[np.ndarray] = None,
        int_array: Optional[np.ndarray] = None,
        quantizer: Optional[Quantizer] = None,
        n_bits: Optional[int] = None,
    ):
        """使用浮点数组、整数数组和量化器进行初始化。
        参数：
            float_array（可选[np.ndarray]）：一些浮点值。默认为None。
            int_array（可选[np.ndarray]）：一些量化值。默认为None。
            quantizer（可选[Quantizer]）：一个量化器。默认为None。
            n_bits（可选[int]）：如果quantizer为None，则用于量化的位数。
                默认为None。
        """
        self.float_array = float_array
        self.int_array = int_array
        self.quantizer = quantizer if quantizer is not None else Quantizer(n_bits=n_bits)

这是一个Python 类的构造方法（__init__），核心作用是初始化该类的实例对象，围绕 “浮点数据、量化后整数数据、量化器” 三者建立关联，适配不同的初始化场景。以下是关键解析：

1. 核心功能定位

为类实例绑定 3 个核心属性，同时处理 “是否传入现成量化器” 的分支逻辑 —— 若没传量化器，则自动创建一个新的Quantizer对象，确保实例始终具备量化相关能力。

2. 输入参数解析（均为可选参数，默认None）

参数名	类型	作用
float_array	Optional[np.ndarray]	原始的浮点型数据（如未量化的模型权重 / 特征），最终会绑定为实例属性。
int_array	Optional[np.ndarray]	浮点数据量化后得到的整数型数据（如 8bit/16bit 量化结果），绑定为实例属性。
quantizer	Optional[Quantizer]	现成的Quantizer类实例（若已提前创建好量化器，可直接传入复用）。
n_bits	Optional[int]	量化位数（如 8、16），仅在quantizer=None时生效，用于创建新量化器。

3. 关键逻辑拆解

（1）直接绑定基础属性

将输入的float_array（原始浮点数据）、int_array（量化后整数数据）直接赋值给实例的self.float_array、self.int_array属性，后续可通过实例直接访问这两类数据。

（2）量化器的 “复用 / 新建” 逻辑（核心分支）

使用三目运算符处理量化器的初始化，确保实例必有量化器：

• 若传入了quantizer（非None）：直接将其赋值给self.quantizer（复用已有量化器）；
• 若未传入quantizer（为None）：自动调用Quantizer(n_bits=n_bits)创建一个新的量化器实例，赋值给self.quantizer（依赖外部定义的Quantizer类，n_bits是新量化器的核心参数）。

4. 适用场景

该构造方法适配两种常见初始化需求：

• 场景 1：已有现成量化器 → 直接传入quantizer，无需传n_bits（如 “复用训练好的量化器处理新数据”）；
• 场景 2：无现成量化器 → 不传quantizer，但需传n_bits（如 “首次处理数据，需临时创建对应位数的量化器”）。

5. 依赖前提

需确保外部已定义Quantizer类，且该类的构造方法（__init__）支持接收n_bits参数（如之前代码中compute_scale_zp_from_n_bits关联的量化逻辑，推测Quantizer类会基于n_bits计算量化所需的缩放因子、零点等核心参数）。

@property
    def shape(self) -> Optional[Union[int, Tuple[int]]]:
        """返回DualArray的形状。
        返回：
            Optional[Union[int, Tuple[int]]]：DualArray的形状
        """
        if self.float_array is not None:
            return self.float_array.shape

        elif self.int_array is not None:
            return self.int_array.shape

        else:
            return None

这段代码定义了一个名为shape的属性（property），用于获取DualArray类实例的 “形状”（即数组的维度信息，如 1 维数组(5,)、2 维数组(3,4)等），核心逻辑和作用解析如下：

1. 关键语法：@property 装饰器

@property 是 Python 的内置装饰器，作用是将类的方法伪装成类的属性：

• 调用时无需加括号（如 obj.shape，而非 obj.shape()），用法和普通属性（如obj.name）一致；
• 内部可封装逻辑（比如判断、计算），对外提供统一的属性访问接口，隐藏底层细节。

2. 方法核心逻辑：获取数组形状

shape 属性的核心是 “优先从浮点数组取形状，其次从整数数组取，都没有则返回 None”，具体步骤：

1. 判断 float_array 是否存在

   ：如果self.float_array

   （DualArray 实例的浮点数组属性）不为空，直接返回它的shape（NumPy 数组的shape属性，用于描述维度）；

2. 若浮点数组不存在，判断 int_array：如果self.int_array（实例的整数数组属性）不为空，返回它的shape；

3. 两者都不存在：若实例既没有浮点数组也没有整数数组，返None（表示无有效形状）。

3. 类型注解：明确输入输出类型

• 返回值类型Optional[Union[int, Tuple[int]]]：
  • Optional[...]：表示返回值可能是 “指定类型”，也可能是None；
  • Union[int, Tuple[int]]：表示返回值要么是单个整数（如 1 维数组长度5，部分场景下可能简化表示），要么是整数元组（标准的 NumPy 数组形状，如(3,4)）。

4. 实际作用（结合上下文）

结合你之前提供的代码（compute_scale_zp_from_float_int等函数，涉及 “浮点数组 + 整数数组” 的量化逻辑），DualArray应该是一个 “同时可能存储浮点数据（原始数据）和整数数据（量化后数据）” 的类。

这个shape属性的意义在于：

• 对外提供统一的 “获取形状” 接口，用户无需关心实例实际存储的是浮点还是整数数组，直接通过obj.shape就能拿到维度信息；
• 避免用户分别判断 “该用float_array.shape还是int_array.shape”，降低使用复杂度。

def _ensure_quantized(self, key: str, is_symmetric: bool = True) -> np.ndarray:
        """确保整数表示可用的辅助方法。"""
        if self.int_array is None:
            return self.quantizer.quantize(self.float_array, key=key, is_symmetric=is_symmetric)
        else:
            return self.int_array

功能定位：“确保获取量化后的数据”

这是一个辅助工具方法（命名前缀_通常表示内部使用），作用是返回目标数据的 “整数量化结果”—— 无论当前是否已提前生成过量化数据，最终都能输出可用的量化整数数组。

2. 核心逻辑：二选一的条件分支

方法通过判断 “是否已有现成的量化整数数组”，决定返回什么结果，逻辑非常直接：

条件判断	执行操作	返回结果
self.int_array is None	若没有现成的量化整数，就调用量化器（self.quantizer）的quantize方法，用原始浮点数（self.float_array）实时生成量化整数（需传入key标识和对称量化开关）	实时生成的量化整数数组
else	若已有现成的量化整数（self.int_array已存在），则直接复用，无需重复量化	现成的量化整数数组

3. 关键依赖与参数说明

• self.int_array：类的实例属性，存储 “已生成的量化整数数组”（若为None，表示未提前生成）；
• self.float_array：类的实例属性，存储 “原始未量化的浮点数数组”（量化的数据源）；
• self.quantizer：类的实例属性，是专门负责 “浮点数→整数量化” 的工具对象，提供quantize量化方法；
• key参数：用于标识当前量化任务（可能对应不同数据模块 / 场景，供quantize方法区分逻辑）；
• is_symmetric参数：控制量化类型（对称量化 / 非对称量化），透传给quantize方法，确保量化规则一致。

一句话总结

“能直接拿现成的量化整数就直接拿，没有就用原始浮点数实时生成，最终保证给你一个能用的量化整数数组”。

def _ensure_dequantized(self, key: str, is_symmetric: bool = True) -> np.ndarray:
        """确保整数表示可用的辅助方法。."""
        if self.int_array is not None:
            return self.quantizer.dequantize(
                self.int_array, self.float_array, key=key, is_symmetric=is_symmetric
            )
        else:
            return self.float_array

该函数是一个确保数据以 “解量化后格式”（通常为浮点数）返回的辅助方法，核心逻辑围绕 “数据是否已量化（存在整数数组）” 做分支处理，具体解析如下：

1. 函数基础信息

• 作用域：self 表明是类的成员方法，依赖类实例的内部属性（int_array、float_array）和工具（quantizer）。
• 输入参数
  • key: str：用于定位需解量化的数据（比如多组量化参数对应不同数据时，通过 key 匹配）；
  • is_symmetric: bool = True：指定解量化规则（对称量化 / 非对称量化，与量化时的规则对应，保证精度可逆）。
• 返回值：np.ndarray（NumPy 数组），最终输出一定是 “解量化后的格式”（通常为浮点数，便于后续计算）。

2. 核心逻辑（分支处理）

分支 1：若数据已量化（self.int_array is not None）

• 场景：int_array 是 “量化后的数据”（将原始浮点数压缩为整数存储，用于节省空间或适配特定硬件，比如联邦学习、FHE 加密场景）。
• 处理：调用类实例的quantizer（量化工具）的dequantize方法，将整数数组恢复为原始浮点数格式：
  • 依赖参数：int_array（量化后的整数）、float_array（可能用于提供原始范围等参考信息）、key（匹配量化参数）、is_symmetric（匹配量化时的对称规则）；
  • 目的：通过 “解量化” 逆转量化过程，让数据回到可直接计算的浮点数格式。

分支 2：若数据未量化（self.int_array is None）

• 场景：int_array 不存在，说明数据仍以原始浮点数格式（self.float_array）存储，未经过量化处理。
• 处理：直接返回原始浮点数数组 self.float_array，无需额外操作（已满足 “解量化格式” 的要求）。

3. 核心目的

• 统一数据格式：无论原始数据是 “已量化的整数” 还是 “未量化的浮点数”，调用该方法后，输出格式始终一致（解量化后的浮点数），避免后续代码因 “数据格式不统一” 出现错误；
• 适配下游逻辑：后续流程（如模型推理、数值计算）通常依赖浮点数输入，该方法相当于 “格式转换器”，屏蔽了 “量化 / 未量化” 的差异，降低下游代码的复杂度。

def dequantize(self, key: str) -> DualArray:
        """通过反量化将整数数组转换为浮点数."""
        if self.int_array is not None:
            float_array = self.quantizer.dequantize(self.int_array, self.float_array, key=key)
            return DualArray(float_array=float_array, int_array=None, quantizer=self.quantizer)
        else:
            return self

该函数是量化数据处理类中的 “反量化” 方法，核心作用是将已量化的整数数组（int_array）恢复为原始数值范围的浮点数数组（float_array），同时维护量化器（quantizer）的关联关系，以下是分部分解析：

1. 函数基础信息

• 方法名：dequantize，明确指向 “反量化” 操作（量化的逆过程，量化是将浮点数映射为整数以降低存储 / 计算成本，反量化则是恢复回浮点数）。
• 参数：key: str，用于定位 / 标识当前反量化操作对应的具体量化配置（比如多组量化参数时，通过key匹配对应的缩放因子、零点等）。
• 返回值：DualArray，这是一个 “双数组容器类”（推测包含float_array浮点数数组、int_array整数数组、quantizer量化器三个核心属性）。

2. 核心逻辑（分分支解析）

该函数通过判断当前DualArray实例是否存在 “量化后的整数数组（int_array）”，执行两种不同逻辑：

分支 1：存在int_array（需要执行反量化）

if self.int_array is not None:
    # 1. 调用量化器的反量化方法，将整数数组恢复为浮点数数组
    float_array = self.quantizer.dequantize(self.int_array, self.float_array, key=key)
    # 2. 返回新的DualArray：仅保留恢复后的浮点数数组，清空整数数组（反量化后整数数组已无用）
    return DualArray(float_array=float_array, int_array=None, quantizer=self.quantizer)

• 关键操作：依赖关联的quantizer（量化器）的dequantize方法实现核心计算 —— 本质是用量化时的缩放因子（scale）和零点（zp）反向计算，公式通常为：

  float_value = int_value * scale + zp
  

  （具体需看quantizer.dequantize的实现，但核心逻辑一致）。

• 为何清空int_array？反量化的目标是得到浮点数，保留整数数组无意义，同时符合 “DualArray要么存整数（量化态）、要么存浮点数（原始 / 反量化态）” 的设计逻辑。

分支 2：不存在int_array（无需反量化，直接返回自身）

else:
    return self

• 场景：若当前DualArray的int_array已为None，说明数据本身就是浮点数形态（未量化或已反量化），无需重复操作，直接返回自身实例即可，避免无效计算。

3. 核心作用总结

• 功能层面：完成 “量化整数 → 原始浮点数” 的逆转换，是量化模型推理 / 数据恢复中的关键步骤（比如量化模型计算后需反量化才能得到有实际意义的输出结果）。
• 设计层面：通过DualArray容器维护数据形态（浮点数 / 整数）与量化器的绑定，确保反量化时能复用正确的量化参数，同时保持接口简洁（输入输出均为DualArray，便于链式调用）。

def quantize(self, key: str) -> DualArray:
        """通过量化将浮点数组转换为整数数组."""
        if self.float_array is not None:
            int_array = self.quantizer.quantize(self.float_array, key=key)
            return DualArray(
                float_array=self.float_array, int_array=int_array, quantizer=self.quantizer
            )
        else:
            return self

该函数是量化流程中的核心转换方法，作用是将浮点数据（float_array）转换为整数形式（int_array），并返回包含原始浮点、量化整数及量化器的完整数据结构（DualArray），若无浮点数据则直接返回自身。以下是分部分解析：

1. 函数基本信息

• 函数名：quantize

  明确功能是 “执行量化”—— 量化是机器学习 / 密码学（如 FHE 全同态加密）中常见的操作，目的是将高精度浮点数转为低精度整数，降低计算 / 存储成本或适配硬件需求。

• 参数：self, key: str

  • self：类的实例对象（说明该函数是类的成员方法），可访问实例内的float_array（原始浮点数据）、quantizer（量化器对象，负责具体量化逻辑）。
  • key: str：键值参数，用于传递量化过程中的标识（可能是量化配置的索引、数据分组标识等，具体含义由quantizer.quantize内部逻辑决定）。

• 返回值：DualArray或self

  • 成功量化时返回DualArray（包含原始浮点、量化整数、量化器的 “三合一” 数据结构）；
  • 无浮点数据时返回实例自身（避免空数据错误）。

2. 核心逻辑（分分支解析）

分支 1：有浮点数据（self.float_array is not None）

执行 “量化转换→封装返回” 两步：

1. 量化计算：int_array = self.quantizer.quantize(self.float_array, key=key)
   • 调用实例关联的quantizer（量化器）的quantize方法，将原始浮点数据self.float_array转为整数int_array；
   • 量化器的具体逻辑（如基于前文的compute_scale_zp_from_n_bits计算缩放因子scale和零点zp，再通过 int_array = round(float_array / scale + zp) 完成转换）被封装在quantizer内部，此函数仅负责 “调用” 而非 “实现”，符合 “职责分离” 设计。
2. 返回封装结果：return DualArray(...)
   • DualArray是自定义数据结构，作用是同时保留原始浮点和量化整数（便于后续反向量化（从整数恢复浮点）、精度校验或对比分析），并携带quantizer（确保后续可复用相同量化逻辑）。

分支 2：无浮点数据（self.float_array is None）

直接返回self（实例自身）：

• 边界处理逻辑 —— 当实例中没有原始浮点数据时，无需执行量化，直接返回自身，避免因空数据导致的报错，保证函数调用的安全性。

3. 核心作用与应用场景

• 数据流转：是 “浮点数据→量化整数数据” 的关键节点，承接原始数据与后续整数计算（如 FHE 中仅支持整数运算，需先通过此函数量化浮点模型参数 / 输入）。
• 数据完整性：通过DualArray保留原始浮点和量化器，既支持后续使用量化整数做计算，也支持通过量化器反向恢复浮点（如 float_array = (int_array - zp) * scale），兼顾效率与可回溯性。

4. 与前文量化逻辑的关联

结合你之前提供的compute_scale_zp_from_n_bits（计算量化参数scale和zp），该函数是这些 “底层量化参数计算” 的上层调用入口：

• 底层：compute_scale_zp_* 负责计算 “如何量化”（算scale和zp）；
• 中层：self.quantizer.quantize 负责用scale和zp执行 “浮点→整数” 转换；
• 上层：当前quantize函数负责 “触发转换 + 封装结果”，形成完整的量化链路。

def requant(self, key: str) -> DualArray:
        """在n_bits上对整数值进行重新量化."""
        float_array = self.quantizer.dequantize(
            self.int_array, self.float_array, key=f"dequant_{key}"
        )
        int_array = self.quantizer.quantize(float_array, key=f"quant_{key}")
        return DualArray(
            float_array=self.float_array, int_array=int_array, quantizer=self.quantizer
        )

该函数 requant 是量化数据的 “重新量化” 操作，核心作用是对已量化的数据重新执行 “解量化→再量化” 流程，确保数据在量化精度约束下保持一致性，常见于深度学习模型量化推理中（如调整量化范围、修正量化误差）。以下从函数参数、执行流程、返回值三方面简要解析：

1. 核心前提：关键概念铺垫

• self：函数是类的成员方法，推测所属类是 “量化数据容器”（如封装了浮点原始数据、量化后整数数据、量化器的类）。
• DualArray：推测是自定义数据结构，用于同时存储 “浮点原始数据” 和 “对应量化整数数据”，并关联负责量化 / 解量化的工具（quantizer）。
• quantizer：量化工具实例，封装了 quantize（浮点→整数，量化）和 dequantize（整数→浮点，解量化）的核心逻辑（如按指定位数、对称 / 非对称规则计算缩放因子、零点）。

2. 函数参数

• key: str：标识性字符串，用于区分不同场景下的重新量化操作（如日志打印、量化过程追踪时，通过 key 定位具体步骤，例：dequant_input 表示对输入数据解量化）。

3. 核心执行流程（3 步）

本质是 “先把量化整数恢复成浮点→再把浮点重新量化成整数”，目的是让数据符合当前 quantizer 的量化规则（比如调整量化位数、修正前期量化误差）：

1. 解量化（dequantize）：

   调用 self.quantizer.dequantize，将当前存储的 “量化整数数据（self.int_array）” 恢复为 “浮点数据（float_array）”。

   • 输入：量化整数（self.int_array）、参考浮点（self.float_array，可能用于辅助计算量化参数）、标识 key；
   • 输出：解量化后的浮点数据（float_array）。

2. 重新量化（quantize）：

   调用 self.quantizer.quantize，将第一步恢复的 “浮点数据（float_array）” 重新量化为 “新的量化整数数据（int_array）”。

   • 输入：解量化后的浮点数据（float_array）、标识 key；
   • 输出：重新量化后的整数数据（int_array）。

3. 封装返回（DualArray）：

   用 “原始浮点数据（self.float_array，未改变，保留原始精度参考）”、“重新量化后的整数数据（int_array）”、“原量化器（self.quantizer）”，构建并返回一个新的 DualArray 实例。

4. 返回值

• DualArray 实例

  ：新的 “双数据容器”，其中：

  • float_array：仍沿用原始浮点数据（未修改，确保原始信息不丢失）；
  • int_array：替换为 “重新量化后” 的整数数据（符合当前量化规则）；
  • quantizer：沿用原始量化器（确保后续量化逻辑一致性）。

5. 核心作用场景

• 修正量化误差：多次量化 / 解量化后可能出现误差，重新量化可将数据拉回当前量化规则的精度范围内；
• 调整量化参数：若 quantizer 已更新（如量化位数从 8bit 改为 4bit），通过该操作让旧数据适配新规则；
• 保持数据一致性：在模型推理的不同层之间，确保输入 / 输出数据的量化格式统一。

def exp(self, key: str) -> DualArray:
        """计算指数。"""
        float_array = self._ensure_dequantized(key=key)
        return DualArray(
            float_array=np.exp(float_array),
            int_array=None,
            quantizer=self.quantizer,
        )

该函数是 DualArray 类（推测）的成员方法，核心功能是对实例中存储的指定数据计算指数运算，并返回新的 DualArray 对象，以下是分点解析：

1. 函数基本信息

• 方法名：exp，对应 “exponential（指数）”，明确功能是计算数学中的 e^x（e 为自然常数，约 2.718）。
• 参数：key: str，用于指定要操作的数据源 —— 推测 DualArray 内部可能以键值对形式存储多组数据，通过 key 定位目标数据。
• 返回值：DualArray，保持数据结构一致性，返回包含 “指数运算结果” 的新 DualArray 实例。

2. 核心逻辑拆解

步骤 1：获取解量化的浮点数组

float_array = self._ensure_dequantized(key=key)

• self._ensure_dequantized 是类的内部辅助方法，作用是：根据 key 找到对应数据，并确保数据从 “量化状态”（如之前代码中提到的 int_array，即量化后的整数数组）转换为 “解量化状态”（即 float_array，原始 / 恢复的浮点数组）。
• 为什么需要解量化？因为指数运算属于高精度数学运算，直接对量化后的整数操作会导致严重精度丢失，因此必须先恢复为浮点数再计算。

步骤 2：计算指数并构造新 DualArray

return DualArray(
    float_array=np.exp(float_array),
    int_array=None,
    quantizer=self.quantizer,
)

• np.exp(float_array)：调用 NumPy 库的指数函数，对解量化后的浮点数组中每个元素计算 e^x，得到指数运算结果的浮点数组。
• int_array=None：由于刚完成指数运算，结果尚未进行量化（量化是将浮点数转为整数以适配低精度存储 / 计算的操作），因此暂不设置量化后的整数数组，留空。
• quantizer=self.quantizer：继承原实例的量化器（quantizer，推测是处理 “量化 / 解量化” 逻辑的对象，如之前代码中计算 scale/zp 的逻辑可能封装在此），确保后续若需对新结果量化时，使用与原数据一致的量化规则。

3. 与上下文的关联

结合你之前提供的代码（如 compute_scale_zp_from_float_int 等量化相关函数），可推测该 exp 方法的设计场景是 “支持量化的数值计算框架”（可能用于机器学习、加密计算等场景）：

• DualArray 的核心是同时管理 “浮点数组（高精度原始数据）” 和 “整数数组（低精度量化数据）”，而 exp 方法是该框架中 “数学运算模块” 的一部分，确保运算精度的同时，保持数据结构的统一性。

def sum(self, key: str, axis: Optional[int] = None, keepdims: bool = False) -> DualArray:
        """沿指定轴计算总和."""
        int_array = self._ensure_quantized(key=key)
        float_array = (
            np.sum(self.float_array, axis=axis, keepdims=keepdims)
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        int_array = np.sum(int_array, axis=axis, keepdims=keepdims)
        return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

该函数是量化数据场景下的 “双轨求和工具”，核心作用是同时对 “原始浮点数据” 和 “量化后整数数据” 执行求和操作，并返回包含双轨结果的DualArray对象，确保量化过程中数据计算的一致性。以下是逐部分解析：

1. 函数基本信息

• 功能定位：沿指定维度（axis）计算数据总和，适配 “浮点 + 量化整数” 的双轨数据存储模式。
• 输入参数
  • key: str：索引键，用于从当前对象中获取对应量化数据（通过_ensure_quantized方法）。
  • axis: Optional[int] = None：求和维度，如axis=0表示按行求和、axis=1按列求和，None表示对所有元素求和（默认）。
  • keepdims: bool = False：是否保留求和后的维度形状，True则维度数不变（求和后维度长度为 1），False则压缩求和维度（默认）。
• 返回值：DualArray对象，封装了求和后的 “浮点结果” 和 “量化整数结果”，以及原有的量化器（quantizer）。

2. 核心逻辑拆解

（1）获取量化整数数据：int_array = self._ensure_quantized(key=key)

调用对象内置的_ensure_quantized方法，通过key获取对应数据的量化后整数数组（int_array）。

作用：确保后续求和的整数数据是已完成量化的有效数据，避免使用未量化的原始数据。

（2）计算浮点数据的求和（可选）

float_array = (
    np.sum(self.float_array, axis=axis, keepdims=keepdims)
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 条件判断逻辑：仅当满足两个条件时才计算浮点求和：
  1. self.float_array is not None：当前对象存储了原始浮点数据（非空）；
  2. not isinstance(self.float_array, Tracer)：浮点数据不是Tracer类型（Tracer通常是联邦学习 / FHE 加密场景中的 “追踪器”，此时无需计算浮点结果）。
• 计算方式：用np.sum（NumPy 求和函数）按指定axis和keepdims规则计算浮点总和；不满足条件则浮点结果设为None。

（3）计算量化整数数据的求和

int_array = np.sum(int_array, axis=axis, keepdims=keepdims)

直接对步骤（1）获取的 “量化整数数组” 用np.sum求和，求和规则（axis/keepdims）与浮点求和完全一致。

作用：保证 “浮点结果” 和 “整数结果” 的计算维度、形状完全匹配，后续量化反量化时不会出现维度不兼容问题。

（4）返回双轨结果：return DualArray(...)

将 “浮点求和结果”“整数求和结果” 和 “原量化器” 封装成DualArray对象返回。

• 关键意义：DualArray是量化系统中的核心数据结构，同时保存双轨数据可实现 “浮点精度参考” 与 “整数高效计算” 的平衡（如量化推理中用整数计算提速，用浮点结果验证精度），而quantizer则用于后续可能的反量化（将整数结果转回浮点）。

3. 适用场景

该函数典型用于量化神经网络推理、联邦学习、同态加密（FHE） 等场景 —— 这些场景中常需同时维护 “原始浮点（用于精度校准）” 和 “量化整数（用于高效 / 加密计算）”，求和作为基础运算，需保证双轨数据的同步更新。

def mul(self, other: DualArray, key: str) -> DualArray:
        """计算乘法。"""
        self_int_array = self._ensure_quantized(key=f"{key}_self")
        other_int_array = other._ensure_quantized(key=f"{key}_other")
        float_array = (
            self.float_array * other.float_array
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        int_array = self_int_array * other_int_array
        return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

该函数是 DualArray（双数组，同时存储浮点原始数据和量化整数数据）的乘法运算方法，核心作用是同步计算浮点数据和量化整数数据的乘积，并返回新的 DualArray 实例，以下是分模块解析：

1. 函数基本信息

• 功能定位：实现两个 DualArray 对象（self 自身、other 另一个）的乘法运算，兼顾 “原始浮点精度” 和 “量化整数计算”（适配联邦学习、同态加密等需低精度整数运算的场景）。

• 参数说明

  ：

  • self：当前 DualArray 实例（乘法的左操作数）；
  • other: DualArray：参与乘法的另一个 DualArray 实例（右操作数）；
  • key: str：量化过程的标识键（用于 _ensure_quantized 方法中区分不同运算的量化结果，避免冲突）；

• 返回值：新的 DualArray 实例（存储乘法后的浮点数据和整数数据）。

2. 核心逻辑拆解

（1）确保输入数据已量化（获取整数数组）

self_int_array = self._ensure_quantized(key=f"{key}_self")
other_int_array = other._ensure_quantized(key=f"{key}_other")

• _ensure_quantized 是DualArray的内部方法，作用是保证当前实例已完成量化（即生成 int_array）：
  • 若 self 已存在 int_array（之前已量化），则直接返回该整数数组；
  • 若未量化，则调用实例关联的 quantizer（量化器），将 self.float_array 量化为整数数组并返回；
  • 拼接 key（如 key_self/key_other）是为了给不同操作数的量化结果打标签，避免多轮运算中量化状态混乱。

（2）计算乘法后的浮点数据（保留原始精度参考）

float_array = (
    self.float_array * other.float_array
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 目的：保留原始浮点数据的乘法结果，作为 “真实精度基准”（量化整数运算可能有精度损失，浮点结果用于后续校验或反向传播）；
• 条件判断逻辑：
  • 仅当 self.float_array 非空（存在原始浮点数据），且不是 Tracer 类型（Tracer 是同态加密框架 concrete.fhe 中的 “追踪器”，用于记录运算路径，此时不直接计算浮点值）时，才计算浮点乘积；
  • 否则（无浮点数据或处于追踪模式），浮点结果设为 None。

（3）计算乘法后的量化整数数据（核心运算）

int_array = self_int_array * other_int_array

• 直接对两个量化后的整数数组做元素级乘法，是实际用于低精度计算（如加密场景）的核心操作；
• 注意：整数乘法结果后续可能需要二次量化（需依赖外部 quantizer 处理，当前函数仅完成基础乘法）。

（4）返回新的 DualArray 实例

return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

• 用乘法后的 “浮点结果”“整数结果”，以及当前实例的 quantizer（保证后续量化规则一致），构建并返回新的 DualArray，确保数据结构的统一性。

3. 关键设计意图

• 双数据同步计算：同时维护 “浮点原始数据” 和 “量化整数数据”，既满足精度参考需求，又适配低精度 / 加密运算场景；
• 量化状态安全：通过 _ensure_quantized 和 key 确保运算前数据已量化，避免因未量化导致的整数数据缺失；
• 框架兼容性：对 Tracer 类型的判断，适配了 concrete.fhe（同态加密库）的运算追踪逻辑，避免在追踪阶段执行无效浮点计算。

def matmul(self, other: DualArray, key: str) -> DualArray:
        """计算矩阵乘法."""
        self_int_array = self._ensure_quantized(key=f"{key}_self")
        other_int_array = other._ensure_quantized(key=f"{key}_other")
        float_array = (
            self.float_array @ other.float_array
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        return DualArray(
            float_array=float_array,
            int_array=self_int_array @ other_int_array,
            quantizer=self.quantizer,
        )

该函数是DualArray类（推测）的矩阵乘法方法，核心功能是同时处理量化整数数组（int_array）和原始浮点数组（float_array）的矩阵乘法，并返回新的DualArray对象，适配量化场景（如联邦学习、同态加密中的低精度计算）。以下是逐部分解析：

1. 函数签名与入参

def matmul(self, other: DualArray, key: str) -> DualArray:

• self：当前DualArray实例（包含浮点数组float_array、量化整数数组int_array、量化器quantizer）；
• other: DualArray：参与矩阵乘法的另一个DualArray实例（需与self满足矩阵乘法维度要求）；
• key: str：量化过程的标识键（用于_ensure_quantized方法，确保量化状态一致性，避免重复量化）；
• 返回值：新的DualArray实例（包含乘法结果的浮点数组和整数数组）。

2. 核心步骤 1：确保输入量化（获取整数数组）

self_int_array = self._ensure_quantized(key=f"{key}_self")
other_int_array = other._ensure_quantized(key=f"{key}_other")

• _ensure_quantized(key)：是DualArray类的内部方法（推测），功能是确保当前实例的int_array已正确量化（若未量化则基于quantizer和float_array生成，若已量化则直接返回）；
• 拼接key（如key_self、key_other）：为两个实例的量化过程分配唯一标识，避免不同实例量化状态混淆。

3. 核心步骤 2：计算浮点数组的矩阵乘法（可选）

float_array = (
    self.float_array @ other.float_array
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 逻辑：仅在

  原始浮点数组有效

  时计算浮点结果，否则设为None；

  • 有效条件：self.float_array非空（not None），且不是Tracer类型（Tracer是追踪计算图的对象，常见于自动微分 / 量化训练框架，此时无需实时计算浮点结果，仅需追踪流程）；
  • 计算方式：用@（Python 矩阵乘法运算符）执行原始浮点数组的矩阵乘法，保留高精度结果（用于后续验证、反向传播或未量化场景）。

4. 核心步骤 3：返回新的 DualArray 对象

return DualArray(
    float_array=float_array,  # 步骤3计算的浮点结果（或None）
    int_array=self_int_array @ other_int_array,  # 量化整数数组的矩阵乘法结果
    quantizer=self.quantizer,  # 继承当前实例的量化器（确保新结果的量化规则一致）
)

• 关键逻辑：

  整数数组必计算，浮点数组可选计算

  • int_array：直接用@执行量化整数数组的矩阵乘法（核心输出，用于低精度场景的实际计算，如加密环境下的整数运算）；
  • float_array：仅作为 “参考 / 备份”（如后续需要还原为浮点结果时使用）；
  • 继承self.quantizer：确保新DualArray的量化规则（如缩放因子scale、零点zp）与原始实例一致，避免后续处理精度偏差。

5. 核心设计思路

该方法的本质是 “双轨计算”：

• 量化整数轨（int_array）：面向低精度、高效（或加密）的实际计算，是核心执行路径；
• 原始浮点轨（float_array）：面向高精度参考（如结果校验、训练时的梯度计算），是可选辅助路径；
• 适配量化场景：通过_ensure_quantized和继承quantizer，确保整个乘法过程的量化一致性，避免因量化误差导致结果偏移。

def truediv(self, denominator: Union[int, float], key: str) -> DualArray:
        """计算真除法。"""
        float_array = self._ensure_dequantized(key=key)
        return DualArray(
            float_array=float_array / denominator, int_array=None, quantizer=self.quantizer
        )

该函数是DualArray类（推测是处理 “浮点 + 量化整数” 双数据形态的类）的真除法运算方法，核心作用是对实例关联的浮点数据执行除法，并返回保持量化器关联的新DualArray对象，具体解析如下：

1. 函数基础信息

• 方法名：truediv.

  对应 Python 中的 “真除法”（即/运算符，区别于//整数除法，结果保留小数），推测用于重载DualArray

  实例的/运算。

• 参数

  • self：DualArray类实例本身，代表要执行除法的目标对象。
  • denominator: Union[int, float]：除数，仅支持整数或浮点数（不支持量化整数，确保除法精度）。
  • key: str：索引 / 标识字符串，用于从self中准确获取需要解量化的浮点数据（推测self内部可能按key存储多组数据）。

• 返回值：DualArray对象,包含除法后的浮点结果、空的整数数组，以及原实例的量化器（保持量化逻辑一致性）。

2. 核心逻辑拆解

步骤 1：获取解量化的浮点数据

float_array = self._ensure_dequantized(key=key)

• 调用_ensure_dequantized方法（从命名推测为 “确保解量化”）：若self中key

  对应的原始数据是量化整数（int_array非空），则先通过self.quantizer（量化器）将其反量化为浮点数据；若已是浮点数据，则直接返回。最终得到纯净的float_array（确保除法运算基于连续浮点值，避免量化误差干扰）。

步骤 2：执行真除法并构造新对象

return DualArray(
    float_array=float_array / denominator,  # 浮点数据除以除数，执行真除法
    int_array=None,                        # 整数数组设为空
    quantizer=self.quantizer               # 保留原实例的量化器
)

• 除法运算：仅对浮点数据float_array执行/真除法，结果仍为浮点数组。int_array=None的原因：

  除法后的浮点结果需重新量化才能得到对应整数（需调用量化器的quantize方法），当前步骤仅完成 “除法计算”，未执行量化，因此暂不生成新的int_array，留待后续按需量化。

• 保留self.quantizer：确保新对象后续执行量化时，能沿用原有的量化逻辑（如缩放因子scale、零点zp等参数，参考你提供的compute_scale_zp_from_*量化相关函数）。

3. 核心设计意图

• 分离 “计算” 与 “量化”：先基于浮点数据完成除法（保证计算精度），再将量化步骤后置（避免除法过程中因整数截断丢失精度）。
• 保持数据形态一致性：返回的仍是DualArray对象，可继续参与后续的量化、运算等操作，符合类的设计范式。

def rtruediv(self, numerator: Union[int, float], key: str) -> DualArray:
        """计算反向真除法。."""
        float_array = self._ensure_dequantized(key=key)
        return DualArray(
            float_array=numerator / float_array, int_array=None, quantizer=self.quantizer
        )

该函数是自定义类（推测为量化数组相关类，如封装量化 / 浮点数据的 DualArray 所属父类）的反向真除法方法，用于实现 “外部数值 ÷ 类实例内部数据” 的运算逻辑，核心解析如下：

1. 函数基础信息

要素	说明
方法名	rtruediv：Python 魔法方法，对应反向真除法运算符 /（区别于普通 truediv 的 “实例 ÷ 外部值”，rtruediv 是 “外部值 ÷ 实例”）。
参数	- self：类实例本身，代表运算中的 “除数”（内部存储数据）；- numerator：被除数，支持 int/float 类型（外部输入的数值）；- key：索引 / 标识，用于定位实例内部要参与运算的具体数据（如多组量化数据的区分键）。
返回值	DualArray 类实例：运算结果的封装体，包含浮点结果、空量化整数、原实例的量化器。

2. 核心逻辑分步解析

步骤 1：确保实例内部数据为浮点数（去量化）

float_array = self._ensure_dequantized(key=key)

• 调用实例的 _ensure_dequantized 方法，根据 key 提取内部对应的数据，并确保数据是浮点数格式（若原数据是量化后的整数，会通过量化器的 “去量化逻辑” 恢复为浮点数，避免整数除法导致精度丢失）。
• 示例：若实例内部存储的是量化整数 [2,4]（对应浮点 [0.2, 0.4]），调用后会返回浮点数组 [0.2, 0.4]。

步骤 2：执行反向真除法运算并封装结果

return DualArray(
    float_array=numerator / float_array,  # 核心运算：外部值 ÷ 内部浮点数
    int_array=None,                      # 暂不生成量化整数（结果先以浮点存储）
    quantizer=self.quantizer             # 继承原实例的量化器（后续可按需量化）
)

• 核心运算：numerator / float_array 是逐元素运算（基于 numpy 广播机制，如 numerator=1.0 时，1.0 / [0.2, 0.4] 结果为 [5.0, 2.5]）。

• 结果封装规则

  ：

  • float_array：存储运算后的浮点结果（保证精度，是当前核心输出）；
  • int_array=None：不立即对结果进行量化（仅保留浮点态，后续若需量化，可通过 quantizer 处理）；
  • quantizer=self.quantizer：继承原实例的量化器（确保后续若要量化结果时，使用与原数据一致的量化规则，如量化位数、对称 / 非对称模式等）。

3. 应用场景示例

假设存在类实例 da（内部通过 key="data" 存储浮点数据 [0.2, 0.4]），则：

# 执行 “外部值 ÷ 实例数据”：1.0 ÷ [0.2, 0.4]
result = 1.0 / da  # 等价于 da.__rtruediv__(1.0, key="data")

• result 是 DualArray 实例，其 float_array 为 [5.0, 2.5]，int_array 为 None，quantizer 与 da 一致。

4. 关键设计意图

• 反向运算支持：解决 “外部数值 ÷ 实例数据” 的场景（若不实现 rtruediv，直接写 3 / da 会报错，因 Python 无法识别 “非数值 ÷ 数值” 的逻辑）。
• 精度优先：先将内部数据转为浮点数再运算，避免整数除法误差；同时暂不量化结果（int_array=None），留待后续按需处理（如需要存储时再量化，减少中间步骤的精度损失）。
• 量化逻辑一致性：继承原实例的 quantizer，确保后续量化结果时遵循统一规则，避免因量化器不一致导致的数据偏差。

def transpose(self, axes: Union[Tuple[int], List[int]], key: str) -> DualArray:
        """使用给定的轴对数组进行转置."""
        int_array = self._ensure_quantized(key=key)
        float_array = (
            np.transpose(self.float_array, axes=axes)
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        int_array = np.transpose(int_array, axes=axes)
        return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

该函数是 DualArray（一种同时存储浮点数据和量化整数数据的结构）的转置方法，核心作用是按指定轴对数据转置，同时保持 “浮点 - 整数” 的对应关系和量化配置，以下是分模块简要解析：

1. 函数基本信息

• 功能：对 DualArray 中的浮点数据（float_array）和量化整数数据（int_array）执行转置，返回新的 DualArray。
• 参数
  • axes: Union[Tuple[int], List[int]]：转置的轴顺序（如 (1,0) 表示对 2 维数组交换行和列），与 numpy 的 transpose 轴参数规则一致。
  • key: str：量化相关的标识（用于 _ensure_quantized 方法，确保整数数据是已量化的有效状态）。
• 返回值：新的 DualArray 对象，包含转置后的浮点 / 整数数据，以及原对象的量化器（quantizer）。

2. 核心逻辑拆解

（1）确保整数数据已量化

int_array = self._ensure_quantized(key=key)

调用 _ensure_quantized 方法（DualArray 的内部方法），确保当前对象的 int_array 是已完成量化的有效整数数组（避免使用未量化的无效数据），并赋值给局部变量 int_array。

（2）处理浮点数据转置

float_array = (
    np.transpose(self.float_array, axes=axes)
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 条件判断：仅当浮点数据 self.float_array 非空，且不是追踪器对象（Tracer，用于 FHE 加密追踪的工具） 时，才用 numpy.transpose 对其按 axes 转置。
• 特殊情况：若浮点数据为空，或处于加密追踪状态（Tracer），则转置后仍为 None（避免对无效 / 追踪中的数据误操作）。

（3）处理整数数据转置

int_array = np.transpose(int_array, axes=axes)

直接用 numpy.transpose 对（已确保量化的）整数数组 int_array 按 axes 转置 —— 因为整数数据是量化后的确定值，无需额外条件判断，直接执行转置即可。

（4）返回新的 DualArray

return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

用转置后的浮点 / 整数数据，搭配原对象的 quantizer（量化器，存储缩放因子、零点等量化参数），创建并返回新的 DualArray—— 确保转置后的数据仍能通过原量化规则关联（浮点↔整数的转换逻辑不变）。

3. 关键设计意图

• 保持数据一致性：转置时同时处理浮点和整数数据，确保两者的维度、轴顺序完全对齐（避免 “浮点转置但整数未转置” 的错位问题）。
• 兼容加密追踪场景：对 Tracer 类型的浮点数据特殊处理（设为 None），适配 concrete.fhe 框架的加密追踪逻辑（避免干扰 FHE 计算流程）。
• 复用量化配置：新对象直接继承原 quantizer，确保转置前后的量化规则（如缩放因子 scale、零点 zp）不变，浮点与整数的转换关系不破坏。

def max(self, key, axis: Optional[int] = None, keepdims: bool = None) -> DualArray:
        """计算最大值。"""
        int_array = self._ensure_quantized(key=key)
        float_array = (
            np.max(self.float_array, axis=axis, keepdims=keepdims)
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        int_array = max_fhe_relu(int_array, axis=axis, keepdims=keepdims)
        return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

该函数是双数组（DualArray）结构下的最大值计算方法，核心作用是同时处理浮点型数据（用于精度参考）和量化后的整型数据（适配全同态加密 FHE 场景），确保最大值计算在 “精度参考” 与 “加密兼容” 间同步生效，以下是分模块解析：

1. 函数基础信息

• 归属：某个包含DualArray（双数组，存浮点 + 整型数据）和量化器的类（如 FHE 场景下的量化数据容器）。
• 输入参数
  • key：量化相关的标识 / 密钥（用于后续_ensure_quantized确保整型数据已正确量化）。
  • axis: Optional[int]：计算最大值的维度（如 axis=0 按列算、axis=1 按行算，None 则对全数组算）。
  • keepdims: bool：是否保留计算后的维度（如 2x3 数组按行算最大值，keepdims=True 则输出 2x1，False 输出 1 维数组）。
• 返回值：DualArray实例 —— 包含计算后的浮点数组、整型数组，及原量化器（保证后续数据一致性）。

2. 核心逻辑拆解（3 步）

步骤 1：确保整型数据已量化（_ensure_quantized）

int_array = self._ensure_quantized(key=key)

• 作用：从当前类实例中获取量化后的整型数组（int_array）。
• 背景：FHE 场景中，加密计算仅支持整型数据，因此需先通过 “量化器（quantizer）” 将浮点数据转为整型；_ensure_quantized就是确保这一步已完成，避免后续计算用未量化的无效数据。

步骤 2：计算浮点数组的最大值（用于精度参考）

float_array = (
    np.max(self.float_array, axis=axis, keepdims=keepdims)
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 核心：用 NumPy 的np.max计算原始浮点数组（self.float_array）的最大值，但加了两个条件判断：
  1. self.float_array is not None：确保浮点数组存在（部分场景可能仅用整型数据）；
  2. not isinstance(self.float_array, Tracer)：排除 “追踪器（Tracer）” 类型 ——Tracer是 FHE 框架（如 Concrete FHE）中用于 “追踪计算过程、生成加密电路” 的工具，此时浮点数组可能未实际存储数值，故不计算。
• 目的：浮点数组的最大值是 “精度锚点”，用于后续验证整型计算结果的合理性（避免量化导致的误差过大）。

步骤 3：计算整型数组的最大值（适配 FHE 加密计算）

int_array = max_fhe_relu(int_array, axis=axis, keepdims=keepdims)

• 关键：调用自定义函数max_fhe_relu计算整型数组的最大值。
• 背景：max_fhe_relu是适配 FHE 的 “最大值 + ReLU” 融合函数——FHE 中复杂操作需拆解为简单电路，“求最大值” 常与激活函数（如 ReLU，用于过滤负值）结合优化计算效率，因此该函数本质是 “在指定维度上计算整型数组的最大值，同时隐含 ReLU 的负值过滤逻辑”（确保输出符合 FHE 加密计算的整型要求）。

3. 最终返回：封装为双数组（DualArray）

return DualArray(float_array=float_array, int_array=int_array, quantizer=self.quantizer)

• 作用：将 “浮点最大值（精度参考）”“整型最大值（加密可用）” 和 “原量化器” 重新封装为DualArray，保证后续流程中：
  • 若需进一步加密计算：用int_array；
  • 若需精度校准 / 结果解析：用float_array和quantizer（通过量化器的scale/zp可将整型结果转回浮点，对比原始浮点最大值验证精度）。

核心设计意图

针对全同态加密（FHE）场景的量化计算需求：

• FHE 仅支持整型运算，需先量化浮点数据；
• 但量化会引入误差，因此保留浮点数组的最大值作为 “精度基准”；
• 最终返回双数组结构，既满足 FHE 的整型计算要求，又能通过浮点基准验证结果合理性，平衡 “加密兼容性” 与 “计算精度”。

def sqrt(self, key: str) -> DualArray:
        """计算平方根"""
        float_array = self._ensure_dequantized(key=key)
        return DualArray(
            float_array=np.sqrt(float_array),
            int_array=None,
            quantizer=self.quantizer,
        )

该函数是某个类的成员方法，核心作用是对指定数据（通过key索引）计算平方根，并返回封装了结果的DualArray对象，具体解析如下：

1. 函数签名与核心目标

• 定义格式

  def sqrt(self, key: str) -> DualArray
  

  • self：类的实例对象，表明这是成员方法，可访问类的内部属性 / 方法（如_ensure_dequantized、quantizer）。
  • key: str：输入参数，字符串类型的 “键”，用于索引要计算平方根的目标数据（类似字典的键，定位具体数据）。
  • -> DualArray：返回值类型，表明结果会封装成DualArray对象（从上下文看，该对象应同时支持存储浮点数据float_array和量化数据int_array）。

2. 核心逻辑拆解

步骤 1：获取 “反量化后的浮点数据”

float_array = self._ensure_dequantized(key=key)

• self._ensure_dequantized(key)：类的内部方法，作用是根据key找到目标数据，并确保数据是反量化后的浮点格式（结合上下文的 “量化 / 反量化” 背景：若原始数据是压缩的 “量化整数”，该方法会先将其恢复为原始浮点数据，避免直接对整数算平方根导致精度丢失）。
• 最终得到float_array：待计算平方根的纯浮点数组（np.ndarray类型，参考上下文的compute_scale_zp函数）。

步骤 2：计算平方根并封装为DualArray

return DualArray(
    float_array=np.sqrt(float_array),
    int_array=None,
    quantizer=self.quantizer,
)

• np.sqrt(float_array)：调用 NumPy 的平方根函数，对步骤 1 得到的浮点数组逐元素计算平方根，得到平方根结果的浮点数组。
• 构造DualArray对象时的 3 个参数：
  1. float_array：传入刚计算出的 “平方根浮点结果”，存储原始精度的结果。
  2. int_array=None：量化后的整数数组设为None—— 此时未对平方根结果做 “量化处理”（可能是因为后续需单独处理量化，或当前阶段仅需保留浮点结果）。
  3. quantizer=self.quantizer：传入类实例的quantizer属性（从上下文看，这是负责 “量化 / 反量化” 的工具对象），为后续可能的量化操作预留工具（即使当前int_array为None，也保留量化器引用）。

3. 核心特点与上下文关联

• 与 “量化” 逻辑的衔接：结合背景中compute_scale_zp（计算量化参数）的代码，该sqrt方法是 “量化数据处理流程” 的一部分 —— 先反量化到浮点算精度正确的平方根，再通过DualArray封装（保留量化器），方便后续按需对平方根结果做量化（补全int_array）。
• 精度保障：先反量化再用np.sqrt（浮点计算），避免直接对量化整数算平方根导致的精度损失（如整数 16 的平方根是 4，但若量化后数据有偏移，直接算会出错）。

def _sub_add(self, other: DualArray, factor: int, key: str, requant: bool) -> DualArray:
        """计算加法或减法，可能包含一个重量化步骤."""
        if requant:
            # 如果两个数组尚未反量化，我们会对它们进行反量化处理
            self_float_array = self._ensure_dequantized(key=f"{key}_sub_add_self")
            other_float_array = other._ensure_dequantized(key=f"{key}_sub_add_other")

            if (
                not isinstance(self.int_array, Tracer)
                and not isinstance(self.float_array, Tracer)
                and not f"{key}_sub_add_self" in self.quantizer.scale_dict
            ):
                # 将两个浮点数组合并以进行量化
                self_orig_shape = self_float_array.shape
                other_orig_shape = other_float_array.shape
                combined_array = np.concatenate(
                    [self_float_array.ravel(), other_float_array.ravel()]
                )

                #将两个数组一起重新量化
                combined_int_array = self.quantizer.quantize(
                    combined_array, key=f"{key}_sub_add_requant"
                )

                # 将数组拆分回它们各自的对象
                self_int_array, other_int_array = np.split(
                    combined_int_array, [np.prod(self_orig_shape)]
                )

                # 将量化数组重塑回它们原来的形状
                self_int_array = self_int_array.reshape(self_orig_shape)
                other_int_array = other_int_array.reshape(other_orig_shape)
            else:
                self_int_array = self.quantizer.quantize(
                    self_float_array, key=f"{key}_sub_add_requant"
                )
                other_int_array = self.quantizer.quantize(
                    other_float_array, key=f"{key}_sub_add_requant"
                )
        else:
            self_int_array = self._ensure_quantized(key=f"{key}_quant_self")
            other_int_array = other._ensure_quantized(key=f"{key}_quant_other")

        self_float_array = (
            self.float_array + (factor * other.float_array)
            if (
                not isinstance(self.float_array, Tracer)
                and self.float_array is not None
                and other.float_array is not None
            )
            else None
        )
        return DualArray(
            float_array=self_float_array,
            int_array=self_int_array + (factor * other_int_array),
            quantizer=self.quantizer,
        )

该函数是 DualArray 类（同时存储浮点数组与量化整数数组的数据结构）的核心运算方法，用于统一处理加法 / 减法操作，并根据需求控制是否执行 “重量化” 以保证量化精度，适配可能的全同态加密（FHE）追踪场景（通过 Tracer 类判断）。以下是分模块的简要解析：

1. 核心功能与参数说明

参数	作用
self	当前 DualArray 实例（运算的左操作数）
other	另一个 DualArray 实例（运算的右操作数）
factor	符号控制因子：1 表示 “加法”（self + other），-1 表示 “减法”（self - other）
key	唯一标识键，用于量化过程中记录 / 查询缩放因子（scale），避免重复计算
requant	是否执行 “重量化”：True 需要先反量化再重新统一量化，False 直接用现有量化整数运算

2. 核心逻辑拆解（分requant=True/False两种场景）

场景 1：requant=True（需要重量化，保证运算精度）

当两个 DualArray 的量化参数（缩放因子、零点）可能不一致时，需先统一反量化为浮点数，再合并重新量化，步骤如下：

1. 反量化操作：调用_ensure_dequantized，将self和other的量化整数数组（int_array）转换为原始浮点数数组（float_array），避免量化误差累积。
2. 判断是否需要合并量化
   • 若非 FHE 追踪场景（int_array/float_array不是 Tracer 实例）且无预存缩放因子，将两个浮点数数组展平后合并（np.concatenate），确保用同一套量化参数（基于合并数组的极值），避免分别量化导致的精度丢失。
   • 若是 FHE 追踪场景或有预存缩放因子，直接对两个浮点数数组分别量化（因 FHE 场景需单独追踪每个变量）。
3. 拆分与重塑：合并量化后的整数数组，按原数组长度拆分并恢复原形状，得到适配运算的量化整数（self_int_array/other_int_array）。

场景 2：requant=False（无需重量化，直接用现有量化值）

当两个 DualArray 已确保量化参数一致时，直接调用_ensure_quantized获取各自的量化整数数组（self_int_array/other_int_array），跳过反量化 - 重量化流程，提升效率。

3. 结果计算与返回

1. 浮点结果计算：仅在 “非 FHE 追踪场景” 且浮点数组有效时，计算self.float_array + factor * other.float_array（对应加法 / 减法）；否则浮点结果设为None（FHE 场景优先用整数运算）。
2. 量化整数结果计算：直接执行self_int_array + factor * other_int_array（量化域内的加法 / 减法）。
3. 返回新 DualArray：将计算后的浮点数组、量化整数数组，结合原量化器（self.quantizer）封装为新 DualArray 返回，保证数据结构一致性。

4. 关键设计目的

• 精度保障：通过requant=True的合并量化，避免不同量化参数导致的运算误差。
• FHE 适配：通过 Tracer 实例判断，兼容全同态加密场景下的变量追踪需求（FHE 中需基于整数运算）。
• 灵活性：用factor控制加减，用requant控制是否重量化，适配不同精度 / 效率需求。

def add(self, other: DualArray, key: str, requant: bool = True) -> DualArray:
        """计算加法."""
        return self._sub_add(other=other, factor=1, key=key, requant=requant)

    def sub(self, other: DualArray, key: str, requant: bool = True) -> DualArray:
        """计算减法。."""
        return self._sub_add(other=other, factor=-1, key=key, requant=requant)

    def linear(self, weight: DualArray, bias: DualArray, key: str) -> DualArray:
        """使用一些权重和偏置值计算线性运算."""
        assert bias is not None, "None bias is not supported in the linear op, use matmul instead."

        x_matmul = self.matmul(weight, key=f"linear_matmul_{key}")

        x_linear = x_matmul.add(bias, key=f"linear_add_{key}")

        return x_linear

这段代码定义了三个与DualArray（推测是支持加密 / 量化等特殊能力的数组类型） 相关的方法，核心是封装基础算术运算与线性变换逻辑，实现代码复用与功能模块化，以下是简要解析：

1. 核心背景：DualArray 的定位

从方法参数（如 other: DualArray）和关联操作（量化、矩阵乘法、加密场景常用的 requant 重量化）推测，DualArray 并非普通 NumPy 数组，而是适配联邦学习、同态加密（FHE）或量化模型的特殊数组类 —— 需在运算中处理精度（如重量化）、密钥（key 用于安全操作）等特殊逻辑。

2. 三个方法的具体解析

（1）add(self, other: DualArray, key: str, requant: bool = True) -> DualArray

• 功能：实现两个 DualArray 的加法运算（self + other）。

• 关键逻辑

  不单独写加法逻辑，而是调用底层通用方法_sub_add，通过传入factor=1将加法转化为self + 1*other

  ，实现 “加 / 减法逻辑复用”。

• 参数含义

  • other：待相加的另一个 DualArray；
  • key：安全操作密钥（如加密场景下的运算授权标识）；
  • requant：是否执行 “重量化”（量化模型中，运算后数值可能超出量化范围，需重新调整精度，默认开启）。

（2）sub(self, other: DualArray, key: str, requant: bool = True) -> DualArray

• 功能：实现两个 DualArray 的减法运算（self - other）。
• 关键逻辑：同样复用_sub_add方法，通过传入factor=-1将减法转化为self + (-1)*other，避免重复编写类似的运算校验（如数组形状匹配、加密状态同步）逻辑。
• 参数含义：与 add 完全一致，仅 factor 隐含的运算逻辑不同。

（3）linear(self, weight: DualArray, bias: DualArray, key: str) -> DualArray

• 功能：实现深度学习中经典的线性变换运算（y = x @ weight + bias，即 “矩阵乘法 + 偏置加法”）。

• 关键逻辑（三步）

  ：

  1. 断言校验：通过 assert bias is not None 强制要求传入偏置（若无需偏置，提示用户改用纯矩阵乘法 matmul 方法）；
  2. 矩阵乘法：调用 self.matmul(weight, ...) 计算 self（输入特征）与 weight（权重）的矩阵乘积（即 x @ weight）；
  3. 加偏置：对矩阵乘法结果调用 add(bias, ...)，加上偏置项 bias，得到最终线性变换结果。

• 参数含义

  • weight：线性变换的权重矩阵（DualArray 类型）；
  • bias：线性变换的偏置向量（DualArray 类型，不可为 None）；
  • key：用于子操作（矩阵乘法、加法）的密钥前缀（通过 f"linear_matmul_{key}" 生成子操作唯一密钥，避免冲突）。

3. 整体设计亮点

• 逻辑复用：用 _sub_add 统一实现加 / 减法，减少冗余代码，降低维护成本；
• 场景适配：通过 key（安全）、requant（精度）、bias 校验（功能约束），适配加密 / 量化模型的特殊需求；
• 接口清晰：将 “线性变换” 封装为独立方法，屏蔽 “矩阵乘 + 加偏置” 的底层细节，符合深度学习开发者的使用习惯。

# Concrete-Python不支持numpy.array_split和numpy.take，所以我们需要构建一个自定义的
    # 分割方法来替代
    # FIXME: https://github.com/zama-ai/concrete-internal/issues/329
    def enc_split(self, n: int, axis: int, key: str) -> Tuple[DualArray]:
        """沿着给定的轴将数组分成n个部分."""
        self_int_array = self._ensure_quantized(key=f"{key}_self")

        splitted_float_array = enc_split(self.float_array, n=n, axis=axis)
        splitted_int_array = enc_split(self_int_array, n=n, axis=axis)

        return tuple(
            DualArray(
                float_array=i_float_array,
                int_array=i_int_array,
                quantizer=self.quantizer,
            )
            for i_float_array, i_int_array in zip(splitted_float_array, splitted_int_array)
        )

（“网页解析失败，可能是不支持的网页类型，请检查网页或稍后重试”）及关联的代码、文档信息（文档 URL 指向zama-ai/concrete-internal仓库的 issues#329）来看，当前无法正常获取该网页（issues#329）的完整内容，但结合代码中的注释和逻辑，可做如下简要解析：

1. 核心背景：Concrete-Python（Zama AI 推出的全同态加密框架相关 Python 库）不支持numpy.array_split和numpy.take这两个 NumPy 原生数组操作，而业务中又需要 “分割数组” 的功能，因此需要自定义enc_split方法来替代。代码中 “FIXME” 标注的链接（https://github.com/zama-ai/concrete-internal/issues/329），推测是该框架内部记录 “不支持上述 NumPy 操作” 或 “需完善自定义分割逻辑” 的 issue，用于追踪问题修复进度，但目前该网页因类型不支持等原因解析失败，无法查看 issue 详情。
2. 自定义enc_split方法逻辑：
   • 该方法属于某类的成员函数，作用是 “沿着指定轴（axis）将数组分成 n 个部分”，返回由DualArray（推测是框架自定义的、同时存储浮点数组和量化后整数数组的结构体）组成的元组。
   • 关键步骤：先通过_ensure_quantized确保当前数组已完成量化，得到量化后的整数数组self_int_array；再调用同名的enc_split工具函数（推测是基础的自定义分割逻辑，非成员函数），分别对原始浮点数组（self.float_array）和量化整数数组（self_int_array）进行分割；最后将分割后的浮点、整数数组成对打包成DualArray，组成元组返回，保证分割后的数据仍符合框架的量化 / 加密数据格式要求。

def reshape(self, newshape: Union[int, Tuple[int]], key: str) -> DualArray:
        """将数组重塑为给定的形状."""
        self_int_array = self._ensure_quantized(key=f"{key}_self")

        reshaped_float_array = (
            self.float_array.reshape(newshape)
            if self.float_array is not None and not isinstance(self.float_array, Tracer)
            else None
        )
        reshaped_int_array = self_int_array.reshape(newshape)

        return DualArray(
            float_array=reshaped_float_array,
            int_array=reshaped_int_array,
            quantizer=self.quantizer,
        )

该函数是 DualArray 类（推测为同时存储浮点数据与量化后整数数据的数组类）的重塑方法，核心作用是将数组维度调整为指定形状，同时保持浮点数据、量化整数数据与量化器的关联，以下是分模块解析：

1. 函数签名与核心参数

def reshape(self, newshape: Union[int, Tuple[int]], key: str) -> DualArray:

• self：类实例本身，代表当前要重塑的 DualArray 对象；

  newshape：目标形状，支持两种输入形式：

  • 单个整数（如 3）：将数组重塑为 1 维数组，长度为该整数；
  • 整数元组（如 (2,3)）：将数组重塑为对应维度的多维数组（2 行 3 列）；

• key：标识键，用于后续量化操作的唯一标记（与 _ensure_quantized 方法配合）；

• 返回值：重塑后的新 DualArray 对象，保证数据结构一致性。

2. 关键步骤解析

步骤 1：确保整数数组已量化（_ensure_quantized）

self_int_array = self._ensure_quantized(key=f"{key}_self")

• 调用 _ensure_quantized 方法（DualArray 类的内置方法），确保当前实例的量化整数数组（int_array）已正确生成（避免未量化就操作的错误）；
• 传入带前缀的 key（如原 key 为 reshape1，则变为 reshape1_self），用于区分不同操作的量化记录，便于调试和追溯。

步骤 2：重塑浮点数组（reshaped_float_array）

reshaped_float_array = (
    self.float_array.reshape(newshape)
    if self.float_array is not None and not isinstance(self.float_array, Tracer)
    else None
)

• 浮点数组的重塑需满足两个前提条件，否则设为None
  1. self.float_array is not None：当前实例的浮点数据存在（避免空值错误）；
  2. not isinstance(self.float_array, Tracer)：浮点数据不是 Tracer 类型（Tracer 是 Concrete FHE 库的 “追踪器”，用于记录同态加密操作，此类数据需特殊处理，故暂不重塑）；
• 若满足条件，调用 NumPy 风格的 reshape(newshape) 方法，将浮点数组调整为目标形状；若不满足，浮点数组设为 None（不影响量化整数数组的重塑）。

步骤 3：重塑量化整数数组（reshaped_int_array）

reshaped_int_array = self_int_array.reshape(newshape)

• 直接对步骤 1 得到的 “已量化整数数组” 调用 reshape(newshape)，按目标形状重塑；
• 整数数组是量化后的数据，无 Tracer 或空值限制（因步骤 1 已确保其有效性），故无需额外判断，直接执行重塑。

步骤 4：返回新的 DualArray 对象

return DualArray(
    float_array=reshaped_float_array,
    int_array=reshaped_int_array,
    quantizer=self.quantizer,
)

• 用重塑后的浮点数组、整数数组，搭配原实例的 quantizer（量化器，存储量化参数如 scale、zp），创建并返回新的 DualArray 对象；
• 保留原 quantizer 是关键：确保新数组的量化规则与原数组一致，避免后续量化 / 反量化时出现精度偏差。

3. 核心设计意图

该方法是 **“量化感知” 的数组重塑 **，针对 “浮点数据 + 量化整数数据” 的双存储结构做了特殊适配：

• 对浮点数据：兼容空值和加密追踪场景，避免非法操作；
• 对整数数据：优先确保量化有效性，再执行重塑；
• 最终通过返回新 DualArray，保证数据结构不被破坏，同时支持后续的量化计算（如机器学习、同态加密场景）。

def expand_dims(self, key: str, axis: int = 0) -> DualArray:
        """沿给定轴在数组中添加一个维度。"""
        self_int_array = self._ensure_quantized(key=f"{key}_self")

        return DualArray(
            float_array=np.expand_dims(self.float_array, axis=axis),
            int_array=np.expand_dims(self_int_array, axis=axis),
            quantizer=self.quantizer,
        )

该函数是 DualArray 类（一种同时存储浮点原始数据和量化整数数据的数组类）的成员方法，核心作用是为数组沿指定维度添加一个新维度，且保证浮点数据和量化整数数据的维度操作同步，同时保留量化器信息。以下是分部分解析：

1. 函数基本信息

• 方法名：expand_dims，对应 numpy 中 np.expand_dims（为数组扩维）的逻辑，适配 DualArray 的双数据存储特性。
• 参数
  • key: str：用于量化操作的标识（从 _ensure_quantized 调用推测，作用是标记当前扩维操作对应的量化数据来源，确保量化状态一致性）。
  • axis: int = 0：指定添加新维度的位置，默认在第 0 维（如将形状 (3,4) 的数组扩为 (1,3,4)）。
• 返回值：DualArray 实例，即扩维后新的双数据数组。

2. 核心逻辑拆解

（1）确保量化数据就绪

self_int_array = self._ensure_quantized(key=f"{key}_self")

• 调用 _ensure_quantized 方法（DualArray 类的内部方法），通过拼接 key 生成唯一标识（如 key 为 "input" 时，标识为 "input_self"），确保当前实例的 int_array（量化整数数组）已正确生成且状态有效（避免后续扩维操作使用未量化的无效整数数据）。

（2）生成扩维后的双数据数组

return DualArray(
    float_array=np.expand_dims(self.float_array, axis=axis),
    int_array=np.expand_dims(self_int_array, axis=axis),
    quantizer=self.quantizer,
)

• 对 浮点原始数据 扩维：调用 np.expand_dims 对 self.float_array（原始浮点数据）沿 axis 添加新维度，保持原始数据的数值不变，仅改变形状。
• 对 量化整数数据 扩维：用同样的 axis 对 self_int_array（已确认有效的量化整数数据）扩维，确保浮点数据和整数数据的形状完全同步（避免维度不匹配导致后续量化 / 反量化错误）。
• 保留量化器：将原实例的 quantizer（量化器，存储缩放因子 scale、零点 zp 等量化参数）直接传入新 DualArray，保证扩维前后的量化规则一致（扩维不改变数据的量化逻辑）。

3. 关键作用与场景

• 核心目的：在不破坏 DualArray 「浮点 + 量化整数」双数据绑定特性的前提下，实现数组扩维（如深度学习中为数据添加「批次维度」时，需同时处理输入数据的原始值和量化值）。
• 典型场景：用于联邦学习、同态加密（结合背景中 concrete.fhe 等加密相关库）等需量化数据处理的场景，确保扩维操作不影响后续的加密计算或量化推理。

def slice_array(self, indices: List[List[int]], key: str, axis: int = 0) -> DualArray:
        """沿给定的轴，使用给定的索引对数组进行切片。"""
        self_int_array = self._ensure_quantized(key=f"{key}_self")

        indices = np.array(indices).flatten()

        return DualArray(
            float_array=simple_slice(self.float_array, indices=indices, axis=axis),
            int_array=simple_slice(self_int_array, indices=indices, axis=axis),
            quantizer=self.quantizer,
        )

该函数是 DualArray（双数组，同时存储浮点原始数据和量化整数数据）的核心方法之一，作用是沿指定轴，按给定索引对双数组进行切片操作，最终返回保持相同量化器配置的新 DualArray。以下是分模块的简要解析：

1. 函数基本信息

• 方法归属：DualArray 类的实例方法（第一个参数为 self）。
• 输入参数
  • indices: List[List[int]]：切片用的索引，外层列表嵌套内层列表（后续会展平为一维）；
  • key: str：量化操作的标识（用于 _ensure_quantized 方法，确保切片前整数数组已正确量化）；
  • axis: int = 0：切片的轴（默认沿第 0 轴，如对二维数组的 “行” 切片）。
• 返回值：新的 DualArray 实例（切片后的浮点数组 + 切片后的整数数组 + 原量化器）。

2. 核心逻辑分步解析

步骤 1：确保整数数组已量化（_ensure_quantized）

self_int_array = self._ensure_quantized(key=f"{key}_self")

• 调用 DualArray 的 _ensure_quantized 方法，传入带标识的 key（如原 key 加 _self 后缀）；
• 作用：保证 self（当前双数组）的 int_array（量化整数数组）已生成（若未量化则触发量化逻辑），避免切片时整数数组缺失，最终返回可用的整数数组 self_int_array。

步骤 2：索引格式处理（展平为一维数组）

indices = np.array(indices).flatten()

• 输入的 indices 是「列表嵌套列表」（如 [[0,1], [3,4]]），先转为 numpy 数组，再通过 flatten() 展平为一维数组（如上述示例变为 [0,1,3,4]）；
• 目的：统一索引格式，适配后续 simple_slice 函数对 “一维索引” 的要求，避免嵌套索引导致的切片逻辑混乱。

步骤 3：切片操作与新 DualArray 构造

return DualArray(
    float_array=simple_slice(self.float_array, indices=indices, axis=axis),
    int_array=simple_slice(self_int_array, indices=indices, axis=axis),
    quantizer=self.quantizer,
)

• 核心是调用自定义工具函数simple_slice（从背景代码可知其作用是 “简化数组切片”），对浮点数组和量化整数数组执行「完全相同的切片逻辑」：
  • 对 self.float_array（原始浮点数据）切片，得到切片后的浮点数组；
  • 对 self_int_array（已量化的整数数组）切片，得到切片后的整数数组；
  • 切片时严格使用同一套 indices（展平后的索引）和 axis（指定轴），确保浮点 / 整数数据的 “位置对应关系” 不变（切片后的数据仍能通过量化器关联）。
• 构造新 DualArray 时，复用原实例的 self.quantizer（量化器）：因为切片不改变数据的量化规则（如缩放因子 scale、零点 zp），无需重新创建量化器，保证数据一致性。

3. 关键设计意图

• 双数组同步切片：浮点数组和整数数组必须 “同索引、同轴” 切片，否则会导致两者数据不匹配（如浮点切了第 0/1 行，整数切了第 2/3 行，后续量化 / 反量化会出错）；
• 保持量化状态：通过复用原 quantizer 和提前确保整数数组量化，避免切片后需要重新量化，减少计算开销并保证数据精度；
• 索引兼容性：将嵌套列表索引展平，兼容 simple_slice 函数的输入要求，同时覆盖 “多段离散索引” 的切片场景（如同时切第 0、2、3 行）。

qgpt2_class.py

导入库：

from typing import Any, Dict, Optional  #静态类型检查支持：任意、字典、指定或空

import numpy as np
import torch
from concrete.fhe.compilation import Circuit, Configuration
from concrete.fhe.tracing import Tracer  #编译阶段追踪计算流程（记录运算步骤）
from load_huggingface import get_gpt2_model
from quant_framework import DualArray, Quantizer   #自定义量化框架模块： 
# “双数组” 对象，同时存储浮点原始数据和量化后整数数据，量化器类“整数转浮点”（反量化）操作， “缩放因子” 和 “零点
from transformers.models.gpt2.configuration_gpt2 import GPT2Config

from concrete import fhe

将torch张量的字典转换为DualArray的字典。

def quantize_dict_of_tensors(
    dict_of_tensors: Dict[Any, torch.Tensor], n_bits: int
) -> Dict[Any, DualArray]:
    """将torch张量的字典转换为DualArray的字典。
    参数：
        dict_of_tensors（Dict[Any, torch.Tensor]）：要量化的字典。
        n_bits（int）：量化张量时要考虑的位数。
    返回：
        q_dict（Dict[Any, DualArray]）：量化后的字典。
    """
    q_dict = {
        key: DualArray(float_array=value.detach().cpu().numpy(), n_bits=n_bits)
        for key, value in dict_of_tensors.items()
    }
    return q_dict

该函数是模型量化流程中的核心工具函数，作用是将存储 PyTorch 张量的字典，批量转换为存储自定义DualArray（双数组结构）的字典，为后续量化计算和全同态加密（FHE）适配做准备，具体解析如下：

1. 函数定位与核心目标

   解决 “PyTorch 张量格式” 与 “自定义量化框架格式” 的适配问题 —— 将模型中可能分散在字典里的权重 / 特征张量（torch.Tensor），统一转为同时包含 “原始浮点数据” 和 “量化后整数数据” 的DualArray，方便后续量化参数（缩放因子、零点）的管理。

2. 输入与输出定义

   • 输入dict_of_tensors：键值对结构，键（Any）可自定义（如权重名称），值是待量化的 PyTorch 张量（torch.Tensor，可能是模型权重、中间特征等）；
   • 输入n_bits：量化位数（如 8 位、16 位），决定DualArray中量化整数的精度范围；
   • 输出q_dict：与输入字典结构完全一致（键相同），但值替换为DualArray（存储量化后的数据）。

3. 核心逻辑（字典推导式）

   通过批量遍历字典键值对实现转换，每一步做两件关键操作：

   • 张量格式转换：value.detach().cpu().numpy()—— 将 PyTorch 张量从计算图中分离（detach()）、转移到 CPU（cpu()）、再转为 NumPy 数组（numpy()），消除 PyTorch 依赖，适配DualArray的输入要求；
   • 构造DualArray：用转换后的 NumPy 浮点数组（float_array）和量化位数（n_bits）初始化DualArray，自动完成 “浮点数据→量化整数数据” 的初步封装（DualArray内部会存储两者，供后续使用）。

4. 作用与后续衔接

   输出的q_dict（DualArray字典）可直接用于：

   • 模型权重的量化存储（同时保留原始浮点和量化整数，便于精度对比）；
   • 全同态加密（FHE）前的格式适配（FHE 编译阶段通常依赖 NumPy 数组或自定义结构，而非 PyTorch 张量）。

class QuantizedModel:

量化模型的基类。
量化模型（QuantizedModel）与相关联的量化器（Quantizer）协同工作。该对象主要用于在一个字典中存储所有的缩放因子（scales）和零点（zero points）。借助其唯一键，这些量化参数中的每一个都与特定的量化算子相关联。为了计算并存储这些参数，首先会使用输入集以浮点型进行一次校准过程。之后，在全同态加密（FHE）计算过程中，这些参数会被重新使用，以正确地对数值进行量化和反量化。

def __init__(self, n_bits: int):
        """使用量化器初始化模型。
        参数：
            n_bits（int）：用于初始化量化器的位数。
        """
        self.quantizer = Quantizer(n_bits=n_bits)
        self.x_calib: Optional[torch.Tensor] = None

1. 功能 1：初始化量化器

   self.quantizer = Quantizer(n_bits=n_bits)

   • 为当前QuantizedModel实例创建一个Quantizer（量化器）对象，存入属性self.quantizer；
   • 量化器是模型量化的核心组件，n_bits参数决定了量化精度（如 8 位量化会将浮点数据映射到 0-255 或 - 128~127 的整数范围），这里通过入参n_bits为量化器设定精度。

2. 功能 2：初始化校准数据存储属性

   self.x_calib: Optional[torch.Tensor] = None

   • 定义实例属性self.x_calib，用于后续存储模型校准数据（校准是量化的关键步骤，需用代表性数据确定量化范围）；
   • 类型注解Optional[torch.Tensor]表明该属性可能是torch.Tensor（PyTorch 张量，存储校准数据），也可能是None（初始状态未存储数据时）；
   • 初始值设为None，表示创建实例时暂未传入校准数据。

def finalize(self, x: DualArray):
        """确定输出值。
        如果DualArray的整数数组是Tracer（编译期间使用的对象），则按原样返回它。否则，返回DualArray。这在run_numpy方法的末尾被调用，因为编译器只能将Tracer对象或Numpy数组视为输入和输出。
        参数：
            x（DualArray）：要处理的值。
        返回：
            Union[Tracer, DualArray]：确定后的输出值。
        """
        if isinstance(x.int_array, Tracer):
            return x.int_array
        else:
            return x

该函数是 QuantizedModel 类的核心输出处理方法，作用是根据计算阶段（编译期 / 非编译期）动态调整输出格式，适配全同态加密（FHE）编译需求，具体解析如下：

1. 核心功能

作为量化模型输出的 “格式转换器”，确保不同阶段（FHE 编译 / 常规计算）的输出能被下游流程（如 FHE 编译器、后续模型层）正确识别。

2. 关键参数与返回值

• 输入 x: DualArray：自定义量化框架的核心数据结构，同时存储「浮点原始数据」和「量化后整数数据」（x.float_array 与 x.int_array），是量化 / 反量化过程的载体。

• 返回值 Union[Tracer, DualArray]

  ：二选一的动态类型 ——

  • 编译期返回 Tracer（FHE 编译专用对象）；
  • 非编译期返回完整 DualArray（保留浮点 + 整数数据，供常规计算使用）。

3. 核心逻辑（条件判断）

if isinstance(x.int_array, Tracer):
    return x.int_array  # 编译期逻辑
else:
    return x            # 非编译期逻辑

• 编译期（触发 if 分支）

  FHE 编译阶段会用Tracer对象追踪计算流程（记录运算步骤），且编译器仅支持Tracer或 NumPy 数组作为输入 / 输出。此时需提取DualArray中存储的Tracer类型整数数组，直接返回给编译器，确保编译流程正常执行。

• 非编译期（触发 else 分支）常规计算（如模型校准、非 FHE 推理）无需编译，需保留DualArray的完整信息（浮点 + 整数数据），供后续量化参数传播、反量化等操作使用，因此直接返回原始DualArray

4. 作用场景

主要在 run_numpy 方法（模型核心计算逻辑）末尾调用，是连接 “模型内部量化计算” 与 “下游流程” 的关键节点 —— 既满足 FHE 编译的格式限制，又保证常规计算的数据完整性。

def run_torch(self, inputs: torch.Tensor, fhe: str = "disable", true_float: bool = False):
        """运行量化算子，并附加预处理和后处理步骤。
        此方法用于接收和输出浮点型的torch张量。
        参数：
            inputs（torch.Tensor）：要处理的输入值，为浮点型。
            fhe（str）：要使用的FHE模式，可选值为“disable”“simulate”或“execute”。默认为“disable”。
            true_float（bool）：如果FHE模式设置为“disable”，则指示操作应使用浮点型还是量化型。默认为False。
        返回：
            torch.Tensor：输出值，为浮点型。
        """

        # 将torch张量转换为numpy数组
        inputs = inputs.detach().cpu().numpy()

        #将输入存储为校准值。这样做是为了能够轻松地
        #编译模型而无需手动提取模型的中介隐藏
        #状态。更重要的是，这些值用于转换来自
        #run_numpy方法到它们的DualArray等价物中，因为编译器只接受Numpy数组
        self.x_calib = inputs

        #对输入进行量化
        q_inputs = self.quantizer.quantize(inputs, key="inputs_quant")

        # 如果全同态加密（FHE）模式设置为禁用，我们只需在清晰状态下运行量化算子并进行反量化
        if fhe == "disable":
            q_y = self.run_numpy(q_inputs)

            if true_float:
                # 直接返回输出DualArray的浮点数不会传播量化参数。因此，这些值是仅浮点计算的结果
                y = q_y.float_array

            else:
                # 对输出DualArray进行反量化会传播量化参数。这些值应该代表全同态加密（FHE）计算的预期值，因为它们是仅量化计算的结果。
                y = q_y.dequantize(key="y_dequant").float_array

        # 否则，借助编译步骤构建的全同态加密（FHE）电路需要被调用
        else:
            assert (
                self.circuit is not None
            ), "Module is not compiled. Please run `compile` on a representative inputset."

            # Concrete Python尚未处理批量操作，输入需要逐个进行处理
            y_all = []
            for q_x in q_inputs:

                # 该电路期望在第一个轴上有一个批量大小为1的输入
                q_x = np.expand_dims(q_x, axis=0)

                if fhe == "simulate":
                    q_y = self.circuit.simulate(q_x)

                elif fhe == "execute":
                    q_y = self.circuit.encrypt_run_decrypt(q_x)

                else:
                    raise ValueError(
                        "Parameter 'fhe' can only be 'disable', 'simulate' or 'execute'"
                    )

                # 需要直接调用量化器来对电路的输出进行反量化，因为这里它们被存储在一个NumPy数组中，而不是DualArray对象。
                y_all.append(self.quantizer.dequantize(q_y, key="y_dequant"))

            y = np.concatenate(y_all)

        # 以浮点数形式返回 torch 张量中的值
        return torch.from_numpy(y).type(torch.float32)

该方法是QuantizedModel类的核心接口之一，作用是接收 PyTorch 浮点张量输入，通过量化 / 反量化流程或全同态加密（FHE）流程处理，最终返回 PyTorch 浮点张量输出，本质是为 “量化模型” 提供适配 PyTorch 生态的调用入口，同时兼容 FHE 的加密计算模式。以下从核心逻辑、分支流程、关键细节三方面解析：

一、核心逻辑：输入 - 处理 - 输出的统一链路

无论是否启用 FHE，方法都遵循 “PyTorch 张量→NumPy 数组→量化处理→反量化→PyTorch 张量” 的闭环，解决 “PyTorch 生态输入” 与 “量化 / FHE 计算依赖 NumPy” 的格式适配问题：

1. 输入预处理：先将 PyTorch 张量（inputs）转为 NumPy 数组（detach().cpu().numpy()），剥离计算图、移至 CPU，适配后续量化 / FHE 操作；
2. 校准值存储：将转换后的 NumPy 数组存为self.x_calib，用于后续模型编译（无需手动提取中间隐藏态）和DualArray（量化数据结构）转换；
3. 输入量化：通过self.quantizer.quantize（量化器）将 NumPy 数组转为量化后的数据（q_inputs），为后续计算做准备；
4. 核心处理：根据fhe参数选择 “清晰态计算（FHE 禁用）” 或 “加密态计算（FHE 启用）”；
5. 输出后处理：将最终结果（NumPy 数组）转回 PyTorch 浮点张量（torch.from_numpy(y).type(torch.float32)），符合 PyTorch 调用习惯。

二、两大分支流程：FHE 禁用 vs FHE 启用

方法通过fhe参数（可选 “disable”“simulate”“execute”）区分两种核心处理逻辑，覆盖 “常规测试” 和 “加密部署” 场景：

1. 分支 1：FHE 禁用（fhe == "disable"）—— 清晰态量化计算

适用于模型调试、量化效果验证，不涉及加密，直接在 “明文” 状态下运行量化算子：

• 调用self.run_numpy(q_inputs)：以量化后的数据（q_inputs）调用 NumPy 版本的模型计算逻辑，得到量化输出q_y（DualArray类型，同时存浮点原始数据和量化整数数据）；
• 两种输出选择（由true_float控制）：
  • true_float=True：直接取q_y的浮点原始数据（q_y.float_array），跳过反量化 —— 仅用于纯浮点计算验证，不传播量化参数；
  • true_float=False（默认）：对q_y执行反量化（q_y.dequantize(key="y_dequant")），得到贴合 FHE 计算预期的结果（模拟量化→反量化的完整流程），再取浮点数据。

2. 分支 2：FHE 启用（fhe == "simulate"或"execute"）—— 加密态计算

适用于隐私保护场景（数据不泄露明文），依赖预编译的 FHE 电路（self.circuit）处理：

• 前置校验：先断言self.circuit非空（确保模型已通过compile方法编译，否则报错）；
• 批量处理兼容：因 FHE 框架（Concrete）暂不支持批量操作，需遍历q_inputs逐个处理；
• 两种 FHE 模式：
  • fhe == "simulate"：FHE 模拟运行 —— 用self.circuit.simulate(q_x)在明文状态下模拟加密计算流程，不实际生成密文，用于验证 FHE 电路逻辑；
  • fhe == "execute"：FHE 实际执行 —— 用self.circuit.encrypt_run_decrypt(q_x)完成 “加密→密文计算→解密” 全流程，输出明文结果（q_y）；
• 统一反量化：因 FHE 电路输出是 NumPy 数组（非DualArray），需直接调用self.quantizer.dequantize反量化，再拼接所有结果（np.concatenate(y_all)）。

三、关键细节：适配量化与 FHE 的设计考量

1. DualArray的角色：在 FHE 禁用分支中，q_y是DualArray（同时存浮点和量化整数），既支持直接取浮点（true_float=True），也支持反量化（传播量化参数），兼顾 “纯浮点验证” 和 “量化流程模拟”；
2. FHE 的批量限制：通过for q_x in q_inputs遍历处理，规避 Concrete 框架不支持批量操作的问题，同时用np.expand_dims(q_x, axis=0)给单个输入加 “批量维度 1”，匹配 FHE 电路的输入格式要求；
3. 量化参数一致性：无论哪种分支，反量化都用key="y_dequant"关联量化器参数，确保 “量化→反量化” 的参数统一（如缩放因子、零点），避免计算偏差。

def run_numpy(self, q_inputs: np.ndarray) -> np.ndarray:
        """运行将被转换为FHE的量化算子。
        参数：
            q_inputs（np.ndarray）：量化输入。
        返回：
            np.ndarray：量化输出。
        """
        raise NotImplementedError("This method must be implemented by subclasses.")

这段代码定义了 QuantizedModel 类中的 run_numpy 方法，核心作用是定义 “将被转换为 FHE（全同态加密）的量化算子执行逻辑” 的接口规范，具体解析如下：

1. 方法定位与输入输出：
   • 输入 q_inputs: np.ndarray：明确要求接收 “量化后的输入数据”，且数据类型为 NumPy 数组（适配 FHE 编译对输入格式的要求）；
   • 输出 np.ndarray：规定需返回 “量化后的输出数据”，同样为 NumPy 数组（保证 FHE 计算链路中数据格式的一致性）。
2. 核心功能说明：
   • 方法文档明确其核心用途 —— 承载 “将被转换为 FHE 的量化算子” 的运行逻辑，即后续子类实现时，需在该方法中编写 “量化状态下的模型计算步骤”（如神经网络的卷积、线性层运算等），这些步骤会被 FHE 编译器处理为加密环境下可执行的逻辑。
3. 抽象接口特性（关键）：
   • 方法体内仅执行 raise NotImplementedError(...)，表明这是一个抽象接口方法—— 它只定义了 “要做什么”（运行量化算子以适配 FHE），但不实现 “具体怎么做”；
   • 强制要求子类必须重写该方法：若子类继承 QuantizedModel 却未实现 run_numpy，调用时会抛出错误，确保所有子类都遵循 “适配 FHE 的量化计算逻辑” 的实现规范。
4. 与 FHE 流程的关联：
   • 结合前文 QuantizedModel 类的背景（用于 FHE 场景下的量化模型），该方法是连接 “量化数据” 与 “FHE 编译” 的关键：子类实现的具体计算逻辑，会被 FHE 编译器（如代码中提到的 concrete.fhe）解析、编译为加密环境下可执行的电路，从而实现 “加密数据上的量化模型计算”。

def compile(self, configuration: Optional[Configuration] = None) -> Circuit:
        """使用存储的校准数据编译模型。
        目前，该模型只能在由单个输入组成的批次上进行编译。
        参数：
            configuration（Optional[Configuration]）：编译期间使用的配置。
                默认为 None。
        返回：
            Circuit：底层的全同态加密（FHE）电路。
        """
        assert self.x_calib is not None, "Module is not calibrated."

        # 对校准数据进行量化
        q_inputs = self.quantizer.quantize(self.x_calib, key="inputs_quant")

        # 创建批次大小为1的输入集
        inputset = [np.expand_dims(q_x, axis=0) for q_x in q_inputs]

        # 实例化编译器
        compiler = fhe.Compiler(self.run_numpy, {"q_inputs": "encrypted"})

        # 在校准量化数据上编译电路
        self.circuit = compiler.compile(inputset, configuration=configuration)

        # 打印电路中达到的最大位宽
        print(
            f"Circuit compiled with at most {self.circuit.graph.maximum_integer_bit_width()} bits"
        )

        return self.circuit

该函数是量化模型（QuantizedModel）的 FHE 电路编译核心方法，作用是利用模型已存储的校准数据，将模型转换为可执行全同态加密计算的 “电路（Circuit）”，核心逻辑可拆解为 5 个关键步骤：

1. 校准数据合法性校验

assert self.x_calib is not None, "Module is not calibrated."

• 先通过断言确保模型已完成 “校准”（即 self.x_calib 已存储校准数据，通常来自 run_torch 方法中传入的输入样本）。
• 校准是 FHE 编译的前提：FHE 需基于实际数据分布确定量化范围、位宽等参数，无校准数据会导致量化和电路编译无法适配真实输入，因此直接报错 “模块未校准”。

2. 校准数据量化

q_inputs = self.quantizer.quantize(self.x_calib, key="inputs_quant")

• 调用模型关联的 Quantizer（量化器），将存储的浮点型校准数据（self.x_calib）量化为整数型数据（q_inputs）。
• key="inputs_quant" 用于标记该量化操作对应的参数（如缩放因子、零点），确保后续反量化时能匹配正确的参数。

3. 构造 FHE 编译用的输入集

inputset = [np.expand_dims(q_x, axis=0) for q_x in q_inputs]

• 按注释限制（“仅支持单输入批次编译”），通过 np.expand_dims(q_x, axis=0) 为每个量化后的校准数据（q_x）增加 “批次维度”（轴 0），确保输入格式符合 FHE 编译器对 “单样本批次” 的要求。
• 最终 inputset 是一个列表，每个元素是 “单批次 + 量化后” 的输入数据，用于编译器分析数据范围、优化电路。

4. 实例化编译器并编译电路

# 1. 绑定模型计算逻辑与加密输入标记
compiler = fhe.Compiler(self.run_numpy, {"q_inputs": "encrypted"})
# 2. 用校准输入集编译电路
self.circuit = compiler.compile(inputset, configuration=configuration)

• 编译器绑定：fhe.Compiler接收两个核心参数 ——
  • self.run_numpy：模型的 “numpy 计算逻辑”（即量化后的数据如何通过模型层计算），是电路要 “复现” 的核心逻辑；
  • {"q_inputs": "encrypted"}：标记输入 q_inputs 是 “加密数据”（FHE 电路需明确区分加密 / 明文输入，此处输入需加密，计算过程在密态下进行）。
• 执行编译：调用 compiler.compile，传入 inputset（校准输入集）和可选的 configuration（编译配置，如优化策略、安全参数等），生成 FHE 电路 self.circuit。

5. 输出电路关键信息并返回

print(f"Circuit compiled with at most {self.circuit.graph.maximum_integer_bit_width()} bits")
return self.circuit

• 打印电路的 “最大整数位宽”：FHE 计算中，整数位宽直接影响计算效率和安全性（位宽越大，计算越慢但精度 / 安全性越高），此信息用于调试和性能评估。
• 返回编译好的 Circuit 对象：后续模型在 FHE 模式下（如 fhe="execute"），将直接使用该电路执行密态计算。

核心作用总结

该方法是 “从量化模型到 FHE 可执行电路” 的桥梁 —— 通过校准数据确定量化参数，将模型计算逻辑转换为 FHE 支持的整数电路，并完成编译优化，最终输出可用于密态推理的 FHE 电路。

class QGPT2(QuantizedModel):

实现GPT-2实现中所需量化算子的类

 def __init__(self, n_bits: int, layer: int, n_bits_weights: Optional[int] = None):
        """使用用于量化的一定数量的比特来初始化该类。
        参数：
            n_bits（int）：用于量化输入和激活值的比特数。
            layer（int）：表示要考虑的GPT-2层的索引。
            n_bits_weights（Optional[int]）：用于量化权重的比特数。如果为None，则将使用n_bits。默认为None。
        """
        super().__init__(n_bits=n_bits)
        self.circuit = None
        self.layer = layer

        # 加载模型以获取GPT-2的权重和超参数
        self.float_torch_model = get_gpt2_model("gpt2_model")
        self.hyper_params = self.float_torch_model.config.to_dict()
        self.weights = dict(self.float_torch_model.state_dict())

        # 使用DualArray实例对权重进行量化
        self.q_weights = quantize_dict_of_tensors(
            self.weights, n_bits_weights if n_bits_weights is not None else n_bits
        )

这段代码是 QGPT2 类（基于量化的 GPT-2 模型类）的构造函数，核心作用是初始化量化相关参数、加载原始 GPT-2 模型，并完成权重的量化处理，具体解析如下：

1. 函数定义与参数说明
   • 定义__init__构造函数，接收 3 个参数：
     • n_bits：指定输入和激活值的量化比特数（如 8bit、4bit，用于压缩模型计算量）；
     • layer：指定要处理的 GPT-2 模型层索引（GPT-2 是多层 Transformer 结构，可针对性量化某一层）；
     • n_bits_weights（可选）：指定权重的量化比特数，默认None，此时会复用n_bits的值（实现权重与输入 / 激活值同精度量化）。
2. 父类初始化与基础属性赋值
   • super().__init__(n_bits=n_bits)：调用父类（QuantizedModel，量化模型基类）的构造函数，传递输入 / 激活值的量化比特数，继承基类的量化基础能力；
   • self.circuit = None：初始化 FHE（全同态加密）电路属性为None（后续编译模型时会赋值，用于加密场景下的计算）；
   • self.layer = layer：保存指定的 GPT-2 层索引，用于后续层针对性处理。
3. 加载原始 GPT-2 模型与核心信息
   • self.float_torch_model = get_gpt2_model("gpt2_model")：加载完整的、未量化的 GPT-2 PyTorch 模型（float类型，即 32 位浮点数精度）；
   • self.hyper_params = self.float_torch_model.config.to_dict()：提取模型的超参数（如层数、头数、嵌入维度等）并转为字典，方便后续配置使用；
   • self.weights = dict(self.float_torch_model.state_dict())：提取模型的原始权重（浮点数），转为字典格式存储，为后续量化做准备。
4. 权重量化处理
   • 调用 quantize_dict_of_tensors 函数，将原始浮点数权重字典 self.weights 量化为低比特格式；
   • 量化比特数优先使用 n_bits_weights，若其为None则使用 n_bits；
   • 量化结果存储在 self.q_weights 中，且以 DualArray 类型（推测是支持 “量化值 + 原始信息” 的双结构数组，适配后续计算与反量化）保存。

@property
    def config(self) -> GPT2Config:
        """获取GPT-2的配置。
        返回：
            GPT2Config：GPT-2的配置。
        """
        return self.float_torch_model.config

    def softmax(self, q_x: DualArray):
        """计算softmax函数，使用量化值。
        参数：
            q_x（DualArray）：要考虑的量化值。
        返回：
            q_x_softmax（DualArray）：量化输出。
        """

        # 计算每个序列的最大值
        q_x_max = q_x.max(axis=-1, keepdims=True, key="max")

        # 为了数值稳定性，减去最大值
        q_x_minus_max = q_x.sub(q_x_max, key="sub_max", requant=False)

        # 应用指数函数
        x_exp = q_x_minus_max.exp(key="exp")

        # 沿序列轴计算总和
        q_x_exp_sum = x_exp.sum("sum", axis=-1, keepdims=True)

        # 计算总和的倒数
        x_inverse_exp_sum = q_x_exp_sum.rtruediv(1, key="rtruediv")

        # 计算最终的softmax值
        q_x_softmax = x_exp.mul(x_inverse_exp_sum, key="enc_mul")

        return q_x_softmax

这段代码是 Python 类（结合全同态加密 FHE 与量化 GPT-2 模型场景）中的两个核心成员，分别是属性方法config 和量化 softmax 计算方法softmax，具体解析如下：

1. @property 装饰的 config 方法

核心作用

将config伪装成类的属性（而非普通方法），外部调用时无需加()，直接通过实例.config即可获取 GPT-2 模型的配置，兼顾代码简洁性与逻辑封装。

关键细节

• @property 装饰器：Python 内置语法，将普通方法转换为 “只读属性”—— 调用时像访问属性一样（如obj.config），但实际执行的是方法内部逻辑，避免直接暴露类的私有数据（此处封装了self.float_torch_model.config的获取过程）。
• 返回值类型标注：-> GPT2Config 明确返回值是GPT2Config类的实例，包含 GPT-2 的核心配置（如层数、隐藏层维度、注意力头数等），便于代码类型检查和可读性。
• 功能逻辑：直接返回类中已加载的 PyTorch 版 GPT-2 模型（self.float_torch_model）的配置，本质是对原始模型配置的 “代理访问”，隔离外部与底层模型的直接交互。

2. softmax 方法（量化版本）

核心作用

在量化数据（DualArray 类型） 上计算 softmax 函数，适配全同态加密（FHE）场景下的数值稳定性与量化精度要求（普通 softmax 直接计算易因指数爆炸 / 下溢出错，且量化数据需特殊处理）。

分步逻辑解析

代码步骤	核心操作	目的
q_x_max = q_x.max(...)	沿最后一个维度（axis=-1，通常是序列长度维度）计算最大值，保留维度（keepdims=True）	后续 “减最大值” 时保证张量形状匹配，避免广播错误
q_x_minus_max = q_x.sub(...)	用原始量化值减去最大值，且不重新量化（requant=False）	数值稳定性关键：避免指数函数计算时因数值过大导致溢出（e^x当 x 大时会急剧增大）
x_exp = q_x_minus_max.exp(...)	对 “减最大值后的数据” 计算指数	执行 softmax 的分子部分（softmax 公式：exp(x_i - max_x) / sum(exp(x_j - max_x))）
q_x_exp_sum = x_exp.sum(...)	沿最后一个维度求和	计算 softmax 的分母部分（所有分子的总和）
x_inverse_exp_sum = q_x_exp_sum.rtruediv(1, ...)	计算 “总和的倒数”（即1/总和）	避免直接用分子除以总和（通过 “乘倒数” 简化量化场景下的计算，减少精度损失）
q_x_softmax = x_exp.mul(...)	指数结果乘总和的倒数	得到最终的量化 softmax 输出，确保结果在[0,1]区间且总和为 1

适配场景

因输入是DualArray（量化数据类型，可能关联 FHE 加密信息），所有操作（max/sub/exp等）均调用该类型的内置方法，而非普通 NumPy/PyTorch 函数 —— 确保量化精度不丢失，且兼容后续 FHE 电路的编译（对应代码开头的模型编译逻辑）。

 def attention(self, q_q: DualArray, q_k: DualArray, q_v: DualArray):
        """transformers中定义的注意力机制，带有量化值。
        参数：
            q_q（DualArray）：要考虑的量化查询投影。
            q_k（DualArray）：要考虑的量化键投影。
            q_v（DualArray）：要考虑的量化值投影。
        """

        # 为了精度稳定性进行重新量化。另一种可能是使用舍入功能
        # 替代
        # q_q、q_k、q_v 预期具有形状（n_batch、n_head、n_seq、n_embed // n_head）
        q_q = q_q.requant(key="q_q")
        q_k = q_k.requant(key="q_k")
        q_v = q_v.requant(key="q_v")

        # 通过计算查询和键的点积来计算分数
        # q_scores的预期形状为（n_batch、n_head、n_seq、n_seq）
        q_scores = q_q.matmul(q_k.transpose(axes=(0, 1, 3, 2), key="transpose_key"), key="qk^T")

        # 为了稳定性，按键维度的平方根进行缩放
        dk = q_k.shape[-1]
        scaled_scores = q_scores.truediv(np.sqrt(dk), "truediv")

        # 使用由1组成的上三角矩阵创建一个因果掩码
        seq_length = q_k.shape[2]
        causal_mask = [[1 if j <= i else 0 for j in range(seq_length)] for i in range(seq_length)]

        # 通常，mask_value被设置为-inf。然而，这会使量化过程不可靠。因此，我们考虑数组中的最小值
        if not isinstance(scaled_scores.float_array, Tracer):
            self.mask_value = scaled_scores.float_array.min()

        # 应用因果掩码机制
        scaled_scores.float_array = np.where(
            causal_mask, scaled_scores.float_array, self.mask_value
        )

        # 应用softmax以获得注意力权重，并重新量化以保证精度稳定性
        q_attention_weights = self.softmax(scaled_scores)
        q_attention_weights = q_attention_weights.requant(key="q_attention_weights_requant")

        #通过将权重投射到值矩阵上来计算输出值
        q_output = q_attention_weights.matmul(q_v, key="matmul_attention_values")

        return q_output

该函数是量化版 GPT-2 模型中的注意力机制实现，核心作用是在 Transformer 架构中，基于量化后的查询（Q）、键（K）、值（V）计算注意力权重并输出最终特征，同时通过量化相关操作平衡模型精度与效率（适配全同态加密 FHE 等场景），以下分步骤解析：

1. 函数基础信息

• 功能定位：实现 Transformer 注意力机制，但输入 / 计算过程均基于DualArray（量化数据结构，需同时存储量化值与原始浮点信息以支持量化操作）。

• 输入参数

  ：

  • q_q/q_k/q_v：分别为量化后的查询投影、键投影、值投影，预期形状为(n_batch, n_head, n_seq, n_embed//n_head)（batch 数、注意力头数、序列长度、单头嵌入维度）。

2. 核心步骤解析

（1）重新量化：保证精度稳定性

q_q = q_q.requant(key="q_q")
q_k = q_k.requant(key="q_k")
q_v = q_v.requant(key="q_v")

• 作用：对输入的 Q/K/V 进行二次量化校准。量化过程中可能因数值范围偏移导致精度损失，requant（重新量化）可调整量化参数（如缩放因子、零点），避免后续计算误差累积，替代简单的 “舍入” 操作（舍入易丢失细节）。

（2）计算注意力分数：Q 与 K 的点积

q_scores = q_q.matmul(q_k.transpose(axes=(0, 1, 3, 2), key="transpose_key"), key="qk^T")

• 关键操作：
  1. q_k.transpose：将 K 的最后两个维度（n_seq、n_embed//n_head）转置为（n_embed//n_head、n_seq），确保 Q（n_seq × d_k）与 K 转置（d_k × n_seq）可矩阵乘法。
  2. matmul：Q 与转置后的 K 做点积，得到注意力分数矩阵q_scores，形状为(n_batch, n_head, n_seq, n_seq)—— 每个元素代表 “第 i 个位置的查询对第 j 个位置的键的关注度”。

（3）分数缩放：避免数值过大导致 softmax 饱和

dk = q_k.shape[-1]  # dk = 单头嵌入维度（n_embed//n_head）
scaled_scores = q_scores.truediv(np.sqrt(dk), "truediv")

• 原理：点积结果会随dk（单头维度）增大而线性增长，易导致数值过大，进而使后续 softmax 函数进入 “饱和区”（梯度趋近于 0，无法更新）。除以√dk可将分数方差归一化到 1 附近，保证数值稳定性。

（4）生成因果掩码：适配 GPT-2 的自回归特性

seq_length = q_k.shape[2]
causal_mask = [[1 if j <= i else 0 for j in range(seq_length)] for i in range(seq_length)]

• 作用：GPT-2 是

  自回归模型

  （生成第 i 个 token 时，不能利用 i 之后的 token 信息）。causal_mask是seq_length×seq_length的上三角矩阵：

  • 元素(i,j)=1：允许第 i 个位置关注第 j 个位置（j≤i，即 “过去 / 当前”token）；
  • 元素(i,j)=0：屏蔽第 i 个位置对第 j 个位置的关注（j>i，即 “未来” token）。

（5）应用因果掩码：替换 “未来” 位置分数

if not isinstance(scaled_scores.float_array, Tracer):
    self.mask_value = scaled_scores.float_array.min()  # 用当前分数的最小值替代-inf
scaled_scores.float_array = np.where(causal_mask, scaled_scores.float_array, self.mask_value)

• 细节：传统注意力中，“未来” 位置分数会设为-inf（softmax 后概率趋近于 0），但量化场景下-inf会破坏量化范围（导致数值溢出或精度崩溃），因此用 “当前分数矩阵的最小值” 替代-inf—— 既屏蔽未来信息，又保证量化数据的有效性。

（6）计算注意力权重：softmax 归一化

q_attention_weights = self.softmax(scaled_scores)
q_attention_weights = q_attention_weights.requant(...)

• 过程：
  1. 调用类内softmax方法（量化版，避免浮点计算），将缩放后的分数归一化为注意力权重（每个位置的权重和为 1，代表对不同 token 的关注比例）；
  2. 再次requant：softmax 后数值范围可能变化，重新量化确保后续与 V 的计算精度。

（7）计算最终输出：权重与 V 的点积

q_output = q_attention_weights.matmul(q_v, key="matmul_attention_values")

• 作用：将注意力权重（n_seq×n_seq）与值矩阵 V（n_seq×d_v）做点积，得到融合注意力信息的输出特征，形状仍为(n_batch, n_head, n_seq, n_embed//n_head)—— 后续会通过 “多头合并”“线性投影” 得到最终层输出。

核心设计亮点

1. 全量化兼容：所有操作基于DualArray，无原生浮点计算，适配 FHE（全同态加密）等对 “整数 / 量化数据” 依赖的场景（FHE 处理浮点效率极低）；
2. 精度保护：通过 “重新量化”“最小值掩码替代 - inf” 等设计，规避量化过程中的精度损失，平衡效率与模型效果；
3. 自回归适配：因果掩码严格限制 “未来信息泄露”，符合 GPT-2 的生成式模型定位。

qgpt2_models.py

from __future__ import annotations  
#启用未来版本的类型注解语法,类内部引用自身、跨类类型标注时，导入此模块避免语法错误

import os  #内置模块，操作系统层面资源，加载模型权重、配置文件等资源的路径管理。
from typing import Optional, Tuple, Union  #明确函数 / 变量的类型：整数或空值、元组、双类型

import numpy as np  #数值计算、数组操作（如矩阵运算、数据预处理），不支持 GPU 加速；
import torch  #张量计算（支持 GPU）、自动求导、神经网络模块，
from concrete.fhe.compilation import Circuit, Configuration  #计算电路，编译配置
from qgpt2_class import QGPT2  #自定义量化版 GPT-2 核心类，封装量化逻辑
from quant_framework import DualArray  #自定义类，二维数组，推测量化参数，缩放因子、零点
from transformers import GPT2LMHeadModel  #带 “语言模型头” 的 GPT-2 模型
from transformers.models.gpt2.configuration_gpt2 import GPT2Config  #GPT-2 的配置类
from transformers.models.gpt2.modeling_gpt2 import GPT2Attention  #原始注意力机制类，基于它改造 “量化注意力类”
from transformers.pytorch_utils import Conv1D  #PyTorch 的 1D 卷积层（GPT-2 中用于实现注意力的线性层
from utils import slice_ordered_dict  #按顺序切割有序字典”（切割 GPT-2 的层权重字典，仅提取某一层的参数）

class QGPT2Attention(GPT2Attention)

用于构建量化注意力机制的torch模块的基类

def __init__(self, config: GPT2Config):
        """初始化基类。
        参数：
            config（GPT2Config）：GPT-2的配置。
        """
        super().__init__(config)

        self.fhe = "disable"
        self.true_float = False

这段代码是QGPT2Attention 类的构造函数（__init__方法），核心作用是初始化量化版 GPT-2 注意力模块的基础属性，具体解析如下：

1. 方法定义与参数

   • def init(self, config: GPT2Config)

     ：__init是 Python 类的初始化方法，创建类实例时自动执行；

     • self：代表类实例本身，用于访问实例属性 / 方法；
     • config: GPT2Config：参数config是 GPT-2 模型的配置对象（来自transformers库），包含模型层数、注意力头数、隐藏层维度等核心参数，为注意力模块初始化提供基础配置。

2. 调用父类构造函数

   • super().__init__(config)：super()用于获取父类（这里是GPT2Attention，即原始 GPT-2 注意力类），通过super().__init__(config)调用父类的初始化方法，继承父类的核心功能（如注意力计算的基础逻辑、基于config初始化的层结构等），避免重复编写原始注意力模块的基础代码。

3. 初始化实例属性

   • self.fhe = "disable"：定义fhe属性（FHE 即 “全同态加密”，用于隐私计算），初始值设为 “disable”，表示默认禁用 FHE 模式（后续可通过set_fhe_mode方法修改为 “simulate” 模拟或 “execute” 执行）；
   • self.true_float = False：定义true_float属性，初始值为False，结合fhe="disable"的默认值，意味着默认不使用纯浮点数计算（而是后续会启用量化计算，符合QGPT2Attention“量化注意力” 的设计目标）。

def set_fhe_mode(self, fhe: str = "disable", true_float: bool = False):
        """设置模块前向传播的FHE模式。
        fhe（字符串）：要考虑的FHE模式，可选“disable”（禁用）、“simulate”（模拟）或“execute”（执行）。
        默认值为“disable”。
        true_float（布尔值）：如果FHE模式设置为“disable”，则指示操作应使用浮点数而非量化。默认值为False。
        """
        assert fhe in [
            "disable",
            "simulate",
            "execute",
        ], "Parameter 'fhe' can only be 'disable', 'simulate' or 'execute'."

        self.fhe = fhe
        self.true_float = true_float

该函数是 QGPT2Attention 类中用于控制注意力模块前向传播时 FHE（全同态加密）模式的核心配置方法，核心作用是通过参数赋值定义模块后续计算是否启用加密、如何处理数据精度，具体解析如下：

1. 函数基础信息

• 功能定位：配置模块的 FHE 运行模式，决定后续计算是否涉及加密逻辑、使用量化数据还是浮点数数据。
• 所属类：QGPT2Attention（量化版 GPT-2 注意力模块类），用于在注意力计算中集成量化与加密能力。

2. 关键参数解析

参数名	类型	默认值	核心作用
self	-	-	类实例自身，用于将配置值赋值给实例属性（self.fhe、self.true_float）
fhe	字符串	"disable"	控制 FHE 模式，仅支持 3 个可选值，通过assert强制校验参数合法性
true_float	布尔值	False	仅在fhe="disable"时生效，决定是否使用浮点数计算（而非量化数据）

3. 核心逻辑拆解

（1）参数合法性校验（assert语句）

通过 assert fhe in ["disable", "simulate", "execute"] 强制限制 fhe 参数的取值范围：

• 若传入非指定值（如 "test"），会直接触发断言错误，提示 “参数 'fhe' 只能是 'disable'/'simulate'/'execute'”，避免非法配置导致后续计算异常。

（2）实例属性赋值

将外部传入的合法配置值，赋值给类实例的属性，供后续前向传播函数（如forward）调用：

• self.fhe = fhe：记录当前 FHE 模式，后续计算会根据该值判断是否启用加密模拟 / 执行。
• self.true_float = true_float：记录 “是否使用浮点数” 的开关，仅在 FHE 禁用时生效（避免加密逻辑与浮点数逻辑冲突）。

4. 不同配置的实际意义

结合参数组合，该函数能实现 3 类核心运行状态，对应注意力模块的不同计算逻辑：

fhe 值	true_float 生效情况	模块运行状态
"disable"	生效（默认 False）	禁用 FHE，不涉及加密；- true_float=False：用量化数据计算（符合 “QGPT2” 量化定位）；- true_float=True：用原始浮点数计算（用于对比量化与非量化效果）。
"simulate"	不生效（FHE 未禁用）	模拟 FHE 模式：不实际执行加密运算，但按加密流程的数值范围 / 精度约束计算（用于调试加密逻辑，避免真实加密的高耗时）。
"execute"	不生效（FHE 未禁用）	执行真实 FHE 模式：对计算过程中的数据进行加密处理（用于隐私保护场景，如联邦学习、敏感数据推理）。

class QGPT2LMHeadModel(GPT2LMHeadModel):

用于在GPT2LMHeadModel的前向传播中集成量化操作的基类.

def __init__(
        self,
        config: GPT2Config,
        n_bits: int,
        attention_module: Union[QGPT2SingleHeadAttention, QGPT2MultiHeadsAttention],
        layer: int = 0,
    ):
        """初始化基类。
        该类本质上会用给定的量化模块覆盖在指定索引的层中找到的GPT-2的注意力模块。
        参数：
            config（GPT2Config）：GPT-2的配置。
            n_bits（int）：用于量化输入、权重和激活的位数。
            attention（Union[QGPT2SingleHeadAttention, QGPT2MultiHeadsAttention]）：要考虑的量化注意力模块。
            layer（int）：表示要考虑的GPT-2层的索引。默认为0。
        """
        assert 0 <= layer <= 11, f"The GPT-2 model only has 12 layers, but got {layer}"

        super().__init__(config)

        self.transformer.h[layer].attn = attention_module(config, n_bits=n_bits, layer=layer)

这段代码是量化版 GPT-2 语言模型头类（QGPT2LMHeadModel）的构造函数，核心作用是 “替换 GPT-2 指定层的原生注意力模块为自定义量化注意力模块”，具体解析如下：

1. 核心功能定位

构造函数的本质是 “模块替换”：在初始化量化版 GPT-2 模型时，将 GPT-2 原生的注意力层（transformer.h[layer].attn），替换为传入的 “量化注意力模块”（attention_module），从而实现注意力层的量化计算（降低模型参数量、计算量，适配低资源场景）。

2. 关键参数解析

参数名	类型 / 可选值	作用
self	-	类实例本身，Python 类方法的默认第一个参数，用于访问类的属性和方法。
config	GPT2Config	GPT-2 的基础配置对象（如模型层数、隐藏层维度、注意力头数等），确保量化模型与原生 GPT-2 结构兼容。
n_bits	int	量化位数（如 4/8/16 位），用于指定输入数据、模型权重、激活值的量化精度（位数越少，量化压缩越明显）。
attention_module	Union[QGPT2SingleHeadAttention, QGPT2MultiHeadsAttention]	要替换的 “量化注意力模块”，支持单头（SingleHead）或多头（MultiHeads）两种量化注意力实现，二选一传入。
layer	int（默认 0）	要替换注意力模块的 “GPT-2 层索引”（GPT-2 原生共 12 层，索引 0-11），默认替换第 1 层（索引 0）。

3. 关键代码逻辑解析

（1）参数合法性校验

assert 0 <= layer <= 11, f"The GPT-2 model only has 12 layers, but got {layer}"

• 作用：强制限制layer的取值范围在 0-11（因 GPT-2 原生模型固定 12 层），避免传入无效层索引导致报错。
• 机制：assert断言若不满足条件（如传入 12），直接抛出异常并提示错误原因。

（2）调用父类构造函数

super().__init__(config)

• 作用：先初始化父类（GPT2LMHeadModel，即原生 GPT-2 语言模型头类），继承父类的基础结构（如 Transformer 编码器、语言模型输出头），避免重复构建原生模块。

（3）核心：替换注意力模块

self.transformer.h[layer].attn = attention_module(config, n_bits=n_bits, layer=layer)

• 拆解：
  1. self.transformer.h[layer]：定位到 GPT-2 的第layer层（transformer是模型主体，h是层列表，索引layer对应具体层）；
  2. .attn：该层的 “原生注意力模块”（父类GPT2LMHeadModel继承的原生结构）；
  3. 赋值右侧：用传入的attention_module（量化注意力类）创建实例，传入配置（config）、量化位数（n_bits）、层索引（layer），最终替换原生注意力模块。

总结

该构造函数是 “量化 GPT-2” 的核心入口之一：通过 “先继承原生模型结构，再替换指定层的注意力模块为量化版本” 的逻辑，实现了对 GPT-2 关键计算层（注意力层）的量化改造，同时通过参数校验确保替换的合法性（层索引、模块类型）。

@property
    def q_attention(self) -> GPT2Attention:
        """获取第一层中的GPT-2注意力模块。
        返回：
            GPT2Attention：该注意力模块。
        """
        return self.transformer.h[0].attn

这段代码是 Python 中 @property 装饰器的典型应用，核心作用是将类的方法伪装成 “属性”，让调用者能以 “访问属性” 的简洁方式（而非 “调用方法”）获取特定数据，同时封装数据获取的逻辑。以下是逐部分解析：

1. 核心装饰器：@property

• 作用

  ：将下方定义的q_attention方法 “转化” 为类的只读属性.原本若定义成普通方法（如def get_q_attention(self)），调用时需写obj.get_q_attention()；用@property后，调用时直接写obj.q_attention

  （无括号），更简洁、符合 “属性” 的直觉。

2. 方法定义：def q_attention(self) -> GPT2Attention

• self：类方法的必选参数，代表当前类的实例（通过实例调用时自动传入）。
• -> GPT2Attention：Python 的类型注解，仅用于提示返回值类型（非强制约束），表明该属性最终返回的是 GPT2Attention 类的实例（即 GPT-2 的注意力模块对象）。

3. 文档字符串："""获取第一层中的GPT-2注意力模块..."""

• 作用：遵循 Python 代码规范（PEP 257），用文档字符串（docstring）说明该属性的功能和返回值，方便开发者通过工具（如 help()、IDE 提示）快速理解用途，提升代码可维护性。

4. 核心逻辑：return self.transformer.h[0].attn

• 这是该属性的 “数据来源”，本质是从当前类实例（self）中，按层级获取 GPT-2 模型的第一层注意力模块：
  • self.transformer：当前类（结合背景可知是 QGPT2LMHeadModel，基于 GPT-2 封装）实例中，存储 GPT-2 核心结构的属性（Transformer 编码器主体）；
  • self.transformer.h：h 通常是 GPT-2 编码器的 “层列表”（h 即 hidden layers），列表中每个元素对应一层编码器；
  • self.transformer.h[0]：取列表的第 0 个元素，即 GPT-2 的第一层编码器；
  • self.transformer.h[0].attn：在第一层编码器中，attn 是存储 “注意力模块”（GPT2Attention 实例）的属性，最终将其返回。

总结核心价值

• 简化调用：调用者无需关心 “如何获取第一层注意力模块” 的细节，只需通过 obj.q_attention 直接拿到结果；
• 封装逻辑：若未来 “获取第一层注意力模块” 的路径变化（如属性名修改），只需修改 q_attention 方法内部的返回逻辑，无需修改所有调用它的代码（解耦）；
• 类型清晰：通过类型注解和文档字符串，明确返回值类型，降低协作时的理解成本。

def set_fhe_mode(self, fhe: str = "disable", true_float: bool = False):
        """设置模块前向传递的FHE模式。

fhe（str）：要考虑的FHE模式，"disable", "simulate", or "execute"。默认
“禁用”。
true_float（bool）：如果FHE模式设置为“禁用”，则指示操作是否
应该是浮点而不是量化。默认为假。
        """
        self.q_attention.set_fhe_mode(fhe=fhe, true_float=true_float)

这段代码是 QGPT2LMHeadModel 类（量化版 GPT-2 语言模型头类）中的方法，核心作用是统一控制模型内量化注意力模块（q_attention）的 FHE 运行模式，具体解析如下：

1. 方法定位与功能

   • 方法名 set_fhe_mode：“设置 FHE 模式”，是模型对外暴露的 “控制接口”—— 通过调用它，可直接修改内部量化注意力模块的运行规则，无需单独操作注意力模块本身。
   • FHE（全同态加密）：此处是模型的一种特殊运行状态（用于隐私计算场景，如加密数据上的模型推理），该方法就是切换 “是否启用 / 如何模拟 FHE” 的开关。

2. 参数含义

   fhe: str = "disable"：

   控制 FHE 的核心模式，仅支持 3 种固定值（通过原代码注释或逻辑可推断为枚举类性质）：

   • "disable"（默认）：关闭 FHE 模式，注意力模块按常规逻辑运行；

   • "simulate"：模拟 FHE 模式（不实际执行加密计算，仅模拟 FHE 环境下的计算流程，用于调试 / 性能预估）；

   • "execute"：实际执行 FHE 加密计算（用于真实隐私推理场景）。

   • true_float: bool = False：仅在fhe="disable"（关闭 FHE）时生效的 “补充开关”：

     • False（默认）：关闭 FHE 后，注意力模块仍用量化计算（符合 “QGPT2” 量化模型的核心设计）；
     • True：关闭 FHE 后，注意力模块临时切换为纯浮点计算（用于对比 “量化” 与 “浮点” 的性能 / 精度差异，或临时兼容非量化场景）。

3. 核心逻辑

   • 方法体仅 1 行：

     self.q_attention.set_fhe_mode(fhe=fhe, true_float=true_float)
     

     意思是 “将当前方法接收的fhe和true_float参数，直接传递给模型内部的量化注意力模（self.q_attention

     ）的同名方法”—— 本质是 “代理转发”，保证模型层级的配置能同步到核心的注意力模块，避免参数不一致。

def compile(
        self, inputset_ids: torch.Tensor, configuration: Optional[Configuration] = None
    ) -> Circuit:
        """使用存储的校准数据编译模型。
        参数：
            inputset_ids（torch.Tensor）：要作为输入集考虑的令牌ID。
            configuration（Optional[Configuration]）：编译期间要使用的配置。
                默认为None。
        返回：
            Circuit：底层的FHE电路。
        """

        # 禁用FHE执行，因为下面的前进传递应该是明确的
        #浮点值。这样做是为了正确校准和存储
        #刻度和零点等量化参数
        self.set_fhe_mode(fhe="disable", true_float=False)

        # 在明文状态下执行完整的一次传递
        self.forward(inputset_ids, use_cache=False)

        # 使用存储的校准数据（由中间隐藏状态组成）编译注意力模块
        return self.q_attention.q_module.compile(configuration=configuration)

这段代码是量化 GPT-2 模型中用于编译 FHE（全同态加密）电路的核心方法，核心目的是利用校准数据完成 FHE 电路构建，为后续加密推理做准备，具体解析如下：

1. 方法核心功能

接收输入令牌 ID 和可选的 FHE 配置，通过 “明文校准→参数存储→电路编译” 三步，生成可用于加密推理的底层 FHE 电路。

2. 关键代码逻辑拆解

（1）禁用 FHE 并固定量化模式

self.set_fhe_mode(fhe="disable", true_float=False)

• 作用：强制模型进入明文推理模式，且明确使用 “量化计算” 而非 “纯浮点计算”。
• 原因：FHE 编译前需要先 “校准量化参数”（如前面代码提到的 “缩放因子、零点”），只有在明文 + 量化模式下，才能准确统计中间层（如注意力层）的数值分布，从而确定合理的量化参数并存储。

（2）明文执行一次完整前向传播

self.forward(inputset_ids, use_cache=False)

• 作用：用输入的 “令牌 ID 集合（inputset_ids）” 跑一次完整的模型推理（不缓存中间结果，避免干扰校准）。
• 本质：这是 “校准过程”—— 通过这次前向，模型会自动记录中间隐藏层（尤其是注意力层）的数值特征，将其作为 “校准数据” 存储起来（比如存在q_attention模块中），为后续 FHE 电路适配提供依据。

（3）基于校准数据编译 FHE 电路

return self.q_attention.q_module.compile(configuration=configuration)

• 作用：调用模型中 “量化注意力模块（q_attention）” 的编译接口，传入 FHE 配置，基于前面存储的校准数据，生成最终的 FHE 电路。
• 关键：FHE 电路的核心是 “适配量化后的计算逻辑”，校准数据确保了电路能匹配模型实际推理时的数值范围，避免加密计算时出现精度丢失或溢出。

3. 输入与返回值

类型	名称	说明
输入参数	inputset_ids	torch 张量，存储 “校准用的令牌 ID”（比如一批样本的 token 序列），用于统计量化所需的数值分布
输入参数	configuration	可选的 FHE 编译配置（如加密参数、计算精度等），默认用系统默认配置
返回值	Circuit	编译好的 FHE 电路对象，后续可直接用于 “加密数据的推理计算”

4. 核心设计思路

FHE 编译的前提是 “让电路适配模型的计算逻辑和数值范围”，因此该方法通过 “先明文校准量化参数→再用校准数据编译电路” 的逻辑，确保生成的 FHE 电路既能正确执行模型计算，又能满足加密推理的安全性和精度要求。

class SingleHeadAttention(QGPT2)

表示使用量化方法实现的单个注意力头的类。第一个投影（由“c_attn”权重表示）也通过量化方法完成。为了正确实现这一点，输入的预期形状为（n_batch，1，n_seq，head_dim），而权重则在正确的索引处提取为适当的形状。

def __init__(self, n_bits: int, layer, n_bits_weights: Optional[int] = None):
        super().__init__(n_bits, layer=layer, n_bits_weights=n_bits_weights)

        #提取嵌入维度和头维度，对于GPT-2模型（使用12个头）来说，这两个维度分别是768和64。
        self.n_embd = self.config.n_embd
        self.head_dim = self.config.n_embd // self.config.n_head

1. 构造方法定义与父类继承

def __init__(self, n_bits: int, layer, n_bits_weights: Optional[int] = None):
    super().__init__(n_bits, layer=layer, n_bits_weights=n_bits_weights)

• 参数含义：

  • self：类实例本身，是 Python 类方法的必传参数，用于访问实例的属性 / 方法；
  • n_bits: int：量化位数（整数类型，必填），通常用于指定模型激活值的量化精度（如 8 位、4 位量化）；
  • layer：层索引 / 层对象（未显式指定类型，必填），指定当前量化操作作用于 GPT-2 的哪一层（如第 3 层、第 5 层）；
  • n_bits_weights: Optional[int] = None：权重量化位数（可选整数类型，默认 None），用于指定模型权重参数的量化精度；若为 None，通常会默认使用n_bits的值（即激活值与权重用同一精度量化）。

• super().__init__(...)：

  调用父类的构造方法，将n_bits、layer、n_bits_weights这三个参数传递给父类，实现父类属性的继承（比如父类中定义的量化配置、层相关基础属性等，无需在子类中重复定义）。

2. 提取 GPT-2 的关键维度参数

#提取嵌入维度和头维度，对于GPT-2模型（使用12个头）来说，这两个维度分别是768和64。
self.n_embd = self.config.n_embd
self.head_dim = self.config.n_embd // self.config.n_head

• 背景前提：

  代码注释已说明，这是针对标准 GPT-2 模型的逻辑 ——GPT-2 基础版（如gpt2）默认有 12 个注意力头（n_head=12），嵌入维度（n_embd）固定为 768。

• 参数含义：

  • self.config：从父类继承的 “模型配置对象”（大概率是GPT2Config类实例），存储了 GPT-2 的所有基础配置（如嵌入维度、头数量、层数等）；
  • self.n_embd = self.config.n_embd：将配置中的 “嵌入维度”（n_embd，即模型输入 / 隐藏层的特征维度）赋值给当前实例的n_embd属性，方便后续计算（如注意力层的矩阵运算）；
  • self.head_dim = self.config.n_embd // self.config.n_head：计算 “注意力头维度”（head_dim）——GPT-2 的嵌入维度会平均分配给所有注意力头，因此用嵌入维度 ÷ 头数量得到单个头的特征维度（标准 GPT-2 中即 768 ÷ 12 = 64），该维度是注意力机制中 “Query/Key/Value” 矩阵运算的核心维度。

总结

这段代码的核心逻辑是：

1. 通过__init__接收量化关键参数，调用父类构造方法完成基础初始化；
2. 从模型配置中提取 GPT-2 的嵌入维度和注意力头维度，为后续该层的量化注意力计算（如 QKV 矩阵量化、注意力分数计算）提供维度依据。

def run_numpy(self, q_inputs: np.ndarray) -> Union[np.ndarray, DualArray]:
        """运行将被转换为FHE的量化算子。
        参数：
            q_inputs（np.ndarray）：量化输入。
        返回：
            Union[np.ndarray, DualArray]：量化输出。
        """

        # 使用存储的校准数据将输入转换为DualArray实例
        # q_x的形状为（n_batch，n_seq，n_embed）
        q_x = DualArray(float_array=self.x_calib, int_array=q_inputs, quantizer=self.quantizer)

        # 提取注意力基础模块名称
        mha_module_name = f"transformer.h.{self.layer}.attn."

        # 使用适当的索引提取查询、键以及值的权重和偏置值
        head_0_indices = [
            list(range(i * self.n_embd, i * self.n_embd + self.head_dim)) for i in range(3)
        ]
        q_qkv_weights = self.q_weights[mha_module_name + "c_attn.weight"].slice_array(
            axis=-1, indices=head_0_indices, key=f"slice_qkv_weights_layer_{self.layer}"
        )
        q_qkv_bias = self.q_weights[mha_module_name + "c_attn.bias"].slice_array(
            axis=-1, indices=head_0_indices, key=f"slice_qkv_bias_layer_{self.layer}"
        )

        # 应用第一个投影以将Q、K和V提取为单个数组
        # q_qkv的形状为（n_batch，n_seq，3*head_dim）
        q_qkv = q_x.linear(
            weight=q_qkv_weights,
            bias=q_qkv_bias,
            key=f"attention_qkv_proj_layer_{self.layer}",
        )

        # 重塑q_qkv以便向注意力机制表明我们只考虑单个头
        # 这里，意味着形状现在是（n_batch，1，n_seq，3*head_dim）
        q_qkv = q_qkv.expand_dims(axis=1, key=f"unsqueeze_{self.layer}")

        # 提取Q、K和V，其形状为（n_batch，1，n_seq，head_dim）
        q_q, q_k, q_v = q_qkv.enc_split(3, axis=-1, key=f"qkv_split_layer_{self.layer}")

        # 应用注意力机制
        q_y = self.attention(q_q, q_k, q_v)

        return self.finalize(q_y)

这段代码是量化 GPT-2 注意力模块中，用于执行可转换为 FHE（全同态加密）的 numpy 端前向计算核心函数，核心作用是对量化输入执行 “QKV 投影 - 注意力计算 - 输出处理” 全流程，具体解析如下：

1. 函数核心定位

• 输入：q_inputs（numpy 数组）—— 已量化的模型输入（非浮点数，是量化后整数表示）；
• 输出：支持两种类型 ——numpy 数组（常规量化输出）或DualArray（自定义类，同时存储浮点数参考值与量化整数，用于量化参数推算 / 校准）；
• 核心目标：用 numpy 实现 “可兼容 FHE 编译” 的量化注意力计算，避免 PyTorch 等框架依赖，确保后续能转换为加密计算逻辑。

2. 关键步骤拆解

（1）输入格式转换：量化输入→DualArray

q_x = DualArray(float_array=self.x_calib, int_array=q_inputs, quantizer=self.quantizer)

• 作用：将纯量化整数输入（q_inputs）封装为DualArray；
• 关键依赖：self.x_calib（校准阶段存储的浮点数参考数据，用于量化精度对齐）、self.quantizer（量化器实例，存储缩放因子、零点等量化参数）；
• 目的：通过DualArray统一管理 “量化整数 + 浮点参考”，为后续线性层、注意力计算提供量化 / 反量化支持。

（2）提取目标层注意力权重 / 偏置

mha_module_name = f"transformer.h.{self.layer}.attn."  # 定位目标层注意力模块路径
head_0_indices = [list(range(i*self.n_embd, i*self.n_embd+self.head_dim)) for i in range(3)]  # Q/K/V各头的索引
q_qkv_weights = self.q_weights[...]  # 提取目标层QKV投影的量化权重
q_qkv_bias = self.q_weights[...]     # 提取目标层QKV投影的量化偏置

• 核心逻辑：定位 GPT-2 模型中指定层（self.layer） 的多头注意力（MHA）模块，按 “单头维度（head_dim）” 提取 Q（查询）、K（键）、V（值）对应的量化权重和偏置；
• 细节：head_0_indices生成 Q/K/V 各 1 组头的索引（推测是单头注意力场景，而非多头），确保只取当前计算所需的权重片段。

（3）QKV 投影计算（线性层）

q_qkv = q_x.linear(weight=q_qkv_weights, bias=q_qkv_bias, ...)

• 作用：对输入q_x执行量化线性变换（即 输入×权重 + 偏置），将输入转换为 Q、K、V 拼接的统一数组（q_qkv）；
• 输出形状：(n_batch, n_seq, 3*head_dim) —— 批量大小 × 序列长度 ×（Q+K+V 的单头维度总和），符合 GPT-2 QKV 投影的输出格式。

（4）维度调整与 Q/K/V 拆分

q_qkv = q_qkv.expand_dims(axis=1, ...)  # 新增“头数”维度，形状变为 (n_batch, 1, n_seq, 3*head_dim)
q_q, q_k, q_v = q_qkv.enc_split(3, axis=-1, ...)  # 按最后一维拆分为Q、K、V，各为 (n_batch, 1, n_seq, head_dim)

• 关键目的：适配单头注意力计算格式 ——
  1. expand_dims(axis=1)新增 “头数” 维度（值为 1，代表单头）；
  2. enc_split(3)按最后一维（3×head_dim）平均拆分，得到独立的 Q、K、V 张量。

（5）注意力计算与输出处理

q_y = self.attention(q_q, q_k, q_v)  # 调用注意力核心逻辑（如Scaled Dot-Product Attention）
return self.finalize(q_y)            # 输出后处理（推测是量化结果整理，如转换为numpy数组或保留DualArray）

• 核心：self.attention是实际的注意力计算实现（如缩放点积），输入为拆分后的量化 Q/K/V；
• 收尾：self.finalize对注意力输出做最终处理，确保输出格式符合函数定义（numpy 数组或 DualArray）。

3. 核心设计意图

• 兼容性：用 numpy 实现而非 PyTorch，是为了适配 FHE 编译工具链（FHE 通常依赖纯数值计算逻辑，避免框架层复杂依赖）；
• 量化优先：全程基于DualArray和量化权重计算，无浮点数冗余操作，确保计算过程可直接映射为 “量化 + 加密” 逻辑；
• 层针对性：通过self.layer定位具体层，支持对 GPT-2 不同层的注意力模块单独处理，灵活性高。

class QGPT2SingleHeadAttention(QGPT2Attention)

一个Torch模块，它通过单个头的量化操作重写了GPT-2的注意力机制

def __init__(self, config: GPT2Config, layer: int, n_bits: int = 16):
        super().__init__(config)

        # 实例化用于注意力机制的量化模块
        self.q_module = SingleHeadAttention(n_bits=n_bits, layer=layer)

        # 定义要使用量化算子考虑的头数
        self.n_qhead = 1

        # 考虑到单个头由量化模块处理，且只需考虑11个浮点头，请定义具有适当形状的新一维卷积算子。
        self.float_embed_dim = self.embed_dim - self.n_qhead * self.head_dim
        self.c_attn_1_11 = Conv1D(3 * self.float_embed_dim, self.embed_dim)
        self.split_size = self.float_embed_dim

这段代码是某个量化版 GPT-2 相关类的构造函数，核心作用是初始化 “量化注意力模块” 与 “浮点数注意力计算层”，实现 “部分注意力头量化、部分保留浮点” 的混合计算逻辑，以下是逐部分解析：

1. 构造函数基础框架

   • def __init__(self, config: GPT2Config, layer: int, n_bits: int = 16)
     

     ：定义构造函数，接收 3 个参数：

     • config: GPT2Config：GPT-2 的全局配置（如嵌入维度、头数等），继承自原始 GPT-2 类的核心配置；
     • layer: int：当前层的索引（用于标识量化模块对应哪一层 GPT-2）；
     • n_bits: int = 16：量化位数，默认 16 位（平衡精度与计算效率，常见于轻量级量化场景）。

   • super().__init__(config)：调用父类（大概率是原始 GPT-2 注意力相关类或自定义基类）的构造函数，继承父类的基础属性（如embed_dim嵌入维度、head_dim单个注意力头维度）。

2. 初始化量化注意力模块

   • self.q_module = SingleHeadAttention(n_bits=n_bits, layer=layer)
     

     ：创建 1 个 “单头量化注意力模块”（SingleHeadAttention），并绑定到当前类的q_module属性：

     • 传入n_bits确定该量化头的量化精度，传入layer标记该模块对应 GPT-2 的第几层；
     • 核心目的：用这个量化模块处理 “部分注意力头”，替代传统全浮点计算，降低该头的计算 / 存储开销。

3. 定义量化头数量与浮点计算维度

   • self.n_qhead = 1：明确当前层仅用1 个量化注意力头（n_qhead即 “量化头数”）；

   • self.float_embed_dim = self.embed_dim - self.n_qhead * self.head_dim
     

     ：计算 “浮点数注意力部分的总嵌入维度”：

     • 原始 GPT-2 的总嵌入维度self.embed_dim = 所有注意力头的维度之和（= 头数 × 单个头维度head_dim）；
     • 这里用 “总维度 - 1 个量化头的维度”，得到剩余需要用浮点数计算的注意力头总维度（即float_embed_dim）。

4. 初始化浮点数注意力的卷积计算层

   • self.c_attn_1_11 = Conv1D(3 * self.float_embed_dim, self.embed_dim)
     

     ：创建 1 个 1D 卷积层（Conv1D），用于浮点数注意力头的 “Q/K/V 矩阵计算”：

     • GPT-2 的注意力层中，c_attn层的核心作用是将输入嵌入映射为 Q（查询）、K（键）、V（值）三个矩阵，因此输出维度是 “3× 单个头总维度”；
     • 这里输出维度设为3 * self.float_embed_dim（对应浮点数部分的 Q/K/V 总维度），输入维度为self.embed_dim（原始总嵌入维度），确保与输入数据维度匹配。

   • self.split_size = self.float_embed_dim：定义后续拆分 Q/K/V 矩阵时的 “浮点数部分拆分尺寸”，确保拆分后浮点数部分的维度与float_embed_dim一致，避免维度不匹配。

核心逻辑总结：

该构造函数通过 “1 个量化头 + 剩余浮点头” 的设计，在不显著损失精度的前提下降低计算成本 —— 用SingleHeadAttention处理 1 个量化头，用c_attn_1_11这个 Conv1D 层处理剩余的浮点头，两者协同完成当前层的注意力计算。

def forward(
        self,
        hidden_states: Optional[Tuple[torch.FloatTensor]],
        layer_past: Optional[Tuple[torch.Tensor]] = None,
        attention_mask: Optional[torch.FloatTensor] = None,
        head_mask: Optional[torch.FloatTensor] = None,
        encoder_hidden_states: Optional[torch.Tensor] = None,
        encoder_attention_mask: Optional[torch.FloatTensor] = None,
        use_cache: Optional[bool] = False,
        output_attentions: Optional[bool] = False,
    ) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:
        """GPT-2专为全同态加密（FHE）计算设计的、具有单个头的多头注意力传递。
        初始实现可在huggingFace的GPT2Attention类中找到。
        """
        if encoder_hidden_states is not None:
            raise ValueError(
                "Class cannot be used as cross attention, please make sure to not instantiate "
                "class with `GPT2Attention(..., is_cross_attention=True)`."
            )

        # 清晰计算第1到第11个头的Q、K、V
        query, key, value = self.c_attn_1_11(hidden_states).split(self.split_size, dim=2)

        # 将它们拆分为11个头
        query = self._split_heads(query, self.num_heads - self.n_qhead, self.head_dim)
        key = self._split_heads(key, self.num_heads - self.n_qhead, self.head_dim)
        value = self._split_heads(value, self.num_heads - self.n_qhead, self.head_dim)

        if layer_past is not None:
            past_key, past_value = layer_past
            key = torch.cat((past_key, key), dim=-2)
            value = torch.cat((past_value, value), dim=-2)

        if use_cache is True:
            present = (key, value)
        else:
            present = None

        if self.reorder_and_upcast_attn:
            raise ValueError("Method 'reorder_and_upcast_attn' is not implemented")

        # 在清晰模式下将多头注意力机制应用于11个头上
        attn_output_1_11, _ = self._attn(query, key, value, attention_mask, head_mask)

        # 使用符合FHE的运算符将注意力应用于第一个头
        attn_output_0 = self.q_module.run_torch(
            hidden_states,
            fhe=self.fhe,
            true_float=self.true_float,
        )

        # 将多个头拼接在一起
        attn_output = torch.cat((attn_output_0, attn_output_1_11), dim=1)

        attn_output = self._merge_heads(attn_output, self.num_heads, self.head_dim)
        attn_output = self.c_proj(attn_output)
        attn_output = self.resid_dropout(attn_output)

        return (attn_output, present)

该函数是适配全同态加密（FHE）的 GPT-2 量化注意力模块前向传播方法，核心作用是接收模型中间特征（hidden_states），通过拆分注意力头、分模式计算（清晰计算 + FHE 兼容计算），最终输出注意力层处理后的特征及缓存信息，以下从核心逻辑、关键步骤、参数与返回值三方面简要解析：

一、核心定位

继承并改造 GPT-2 原生注意力逻辑，核心设计是 “分头部差异化计算”：将注意力头拆分为 “普通头”（1-11 号）和 “FHE 适配头”（0 号），前者用常规方式计算，后者用兼容 FHE 的算子计算，平衡模型性能与 FHE 场景下的加密计算需求（FHE 计算通常更耗时，仅对关键头部适配以降低开销）。

二、关键步骤拆解

1. 禁用交叉注意力

   先判断encoder_hidden_states（编码器特征，用于交叉注意力）是否非空，若存在则抛错 —— 说明该类仅支持 “自注意力”（GPT-2 decoder 默认逻辑），不支持跨模态 / 跨编码器的交叉注意力。

2. 生成 1-11 号头的 Q/K/V

   通过self.c_attn_1_11（专为 1-11 号头设计的线性层）处理输入hidden_states，再按split_size（预设的维度拆分大小）将输出拆分为注意力的查询（query）、键（key）、值（value） 张量。

3. 拆分注意力头 + 处理历史缓存

   • 用_split_heads将 Q/K/V 拆分为 “11 个独立注意力头”（参数self.num_heads - self.n_qhead对应 11 个头的数量），每个头负责不同的特征关注维度；
   • 若layer_past（上一层的 key/value 缓存，用于加速生成式任务）非空，将历史 key/value 与当前 key/value 拼接，避免重复计算。

4. 分模式计算注意力输出

   • 1-11 号普通头：用原生_attn方法计算注意力（如缩放点积注意力），得到attn_output_1_11；
   • 0 号 FHE 适配头：调用self.q_module.run_torch（自定义的 FHE 兼容算子），根据self.fhe（FHE 模式：禁用 / 模拟 / 执行）和self.true_float（是否用浮点数计算），输出符合 FHE 要求的attn_output_0。

5. 合并头部 + 输出处理

   • 用torch.cat将 0 号头与 1-11 号头的输出拼接，再通过_merge_heads将多个头的特征合并为统一维度；
   • 经c_proj（线性投影层）和resid_dropout（残差 dropout 层）处理后，得到最终的注意力层输出attn_output。

6. 缓存标记处理

   若use_cache=True（需要缓存当前 key/value 供下一层使用），则present为当前 key/value；否则为None。

三、参数与返回值

类别	细节
输入参数	- hidden_states：前一层输出的特征张量（核心输入）；- layer_past：历史 key/value 缓存（加速生成任务）；- attention_mask：注意力掩码（屏蔽 padding 等无效 token）；- use_cache：是否缓存当前 key/value；- output_attentions：是否输出注意力权重（此处未实现，仅占位）。
返回值	元组(attn_output, present)：- attn_output：注意力层处理后的特征张量；- present：当前 key/value 缓存（或 None）。

四、核心设计亮点

通过 “部分头部适配 FHE” 的策略，既满足了 FHE 场景下的加密计算需求（0 号头），又通过普通头（1-11 号）维持了模型的计算效率，是 “加密安全性” 与 “模型性能” 的折中设计，常见于需要隐私保护的 AI 推理场景（如医疗、金融领域的敏感数据处理）。

class SingleHeadQGPT2Model(QGPT2LMHeadModel)

具有单个注意力头的QGPT2LMHeadModel实现可以在全同态加密（FHE）中执行。

def __init__(self, config: GPT2Config, n_bits: int = 16, layer: int = 0):
        super().__init__(
            config, n_bits=n_bits, attention_module=QGPT2SingleHeadAttention, layer=layer
        )

这段代码是一个类的构造函数（__init__ 方法），用于初始化该类的实例，核心作用是 “复用父类初始化逻辑并预设关键参数”，具体解析如下：

1. 方法定义核心信息

   • def __init__(self, config: GPT2Config, n_bits: int = 16, layer: int = 0)
     

     ：

     • self：类实例自身的引用（Python 构造函数必需参数，用于访问实例属性 / 方法）；
     • config: GPT2Config：必需参数，传入 GPT-2 模型的配置对象（如模型层数、隐藏层维度等），类型标注确保传入参数符合 GPT2Config 类规范；
     • n_bits: int = 16：可选参数，量化位数（默认 16 位），用于控制模型权重 / 激活值的量化精度（如 16 位量化、8 位量化等）；
     • layer: int = 0：可选参数，目标层索引（默认第 0 层），指定要对 GPT-2 模型的哪一层进行量化改造。

2. 核心逻辑：调用父类构造函数

   • super().__init__(...)：通过 super() 调用当前类的父类的构造函数，实现 “代码复用”（避免重复编写父类已有的初始化逻辑）；
   • 传给父类的参数：
     • config：直接传递 GPT-2 配置对象（父类需用它初始化基础模型结构）；
     • n_bits=n_bits：将当前构造函数接收的 “量化位数” 传给父类（父类需用它配置量化规则）；
     • attention_module=QGPT2SingleHeadAttention：预设量化注意力模块—— 明确告诉父类，使用 QGPT2SingleHeadAttention 这个 “单头量化注意力类”，替换 GPT-2 原始的注意力模块（这是量化改造的核心：用自定义量化注意力层替代原生层）；
     • layer=layer：将当前构造函数接收的 “目标层索引” 传给父类（父类需用它定位到要替换的模型层）。

3. 整体功能总结

   这个构造函数的本质是：定义一个 “简化版初始化接口”—— 用户只需传入 config（必需），或按需调整 n_bits（量化精度）、layer（目标层），即可快速初始化一个 “指定层用单头量化注意力模块” 的 GPT-2 相关模型实例，无需每次手动传入 attention_module 参数（已预设为 QGPT2SingleHeadAttention），降低了使用门槛。

@classmethod
    def from_pretrained(
        cls, pretrained_model_name_or_path: Optional[Union[str, os.PathLike]], *model_args, **kwargs
    ):
        """从预训练文件中加载模型，并手动加载新的Conv1D模块的权重。
        卷积模块必须手动加载适当的权重，这些权重代表11个注意力头，而不是通常的12个，因为Hugging Face对GPT-2的初始实现中并不存在这个模块。
        """

        model = super().from_pretrained(
            pretrained_model_name_or_path=pretrained_model_name_or_path, *model_args, **kwargs
        )

        # 获取适当的注意力权重
        c_attn_params = model.q_attention.c_attn.state_dict()

        # 提取适当的索引和形状
        n_embd = model.config.n_embd
        head_dim = model.config.n_embd // model.config.n_head
        head_1_11_indices = [list(range(i * n_embd + head_dim, (i + 1) * n_embd)) for i in range(3)]

        c_attn_params_1_11 = slice_ordered_dict(c_attn_params, dim=-1, indices=head_1_11_indices)

        # 将权重加载到新的卷积模块中
        c_attn_params = model.q_attention.c_attn_1_11.load_state_dict(c_attn_params_1_11)

        return model

这段代码是 QGPT2LMHeadModel 类（量化版 GPT-2 带语言模型头）的类方法，核心作用是从预训练模型文件加载权重，并适配自定义的 Conv1D 模块（c_attn_1_11），解决了 Hugging Face 原生 GPT-2 实现与自定义量化模块的权重不兼容问题，具体解析如下：

1. 方法本质：@classmethod 与 from_pretrained

• @classmethod：表明这是 “类级别的方法”，不依赖实例，通过 cls（代表当前类，即 QGPT2LMHeadModel）调用，用于创建 / 初始化类实例（这里是加载预训练模型实例）。
• from_pretrained：是 Hugging Face transformers 库的 “标准接口”，用于从本地路径或远程仓库（如 Hugging Face Hub）加载预训练模型的权重和配置，这里重写该方法以适配自定义逻辑。

2. 核心逻辑步骤

步骤 1：调用父类方法，加载基础预训练模型

model = super().from_pretrained(...)

• super().from_pretrained：调用父类（Hugging Face 原生 GPT2LMHeadModel）的方法，先正常加载预训练模型的基础权重和配置（如模型结构、原生注意力层权重等），得到一个基础模型实例 model。

步骤 2：提取原生注意力层的权重（c_attn）

c_attn_params = model.q_attention.c_attn.state_dict()

• model.q_attention：自定义量化注意力模块（QGPT2Attention 相关）的实例，是 QGPT2LMHeadModel 中替换原生注意力层的核心组件。
• c_attn：原生 GPT-2 注意力层的 Conv1D 模块（负责注意力的 “查询 / 键 / 值”（QKV）映射），state_dict() 是 PyTorch 中获取模块权重的方法，这里拿到该模块的所有权重（如权重矩阵、偏置等）。

步骤 3：计算 “适配 11 个注意力头” 的权重索引

# 1. 从模型配置中获取关键参数
n_embd = model.config.n_embd  # GPT-2的隐藏层维度（如768，原生GPT-2-small配置）
head_dim = n_embd // model.config.n_head  # 单个注意力头的维度（如768//12=64，原生12头）
# 2. 生成“排除第1个头、保留第2-12头（共11头）”的索引
head_1_11_indices = [
    list(range(i * n_embd + head_dim, (i + 1) * n_embd)) 
    for i in range(3)
]

• 核心目的：从原生 12 头的权重中，剔除第 1 个头，保留后 11 个头的权重（因自定义模块 c_attn_1_11 只需要 11 头，而非原生 12 头）。

• 索引逻辑：

  原生c_attn的权重维度与n_embd * 3（对应 Q、K、V 三个映射，各占n_embd维度）一致；每个映射的n_embd又拆分为 12 头（每头head_dim维度），因此 “跳过第 1 头（前head_dim维度）、取剩余 11 头”，生成 Q/K/V 三个映射的目标索引。

步骤 4：切割权重并加载到自定义模块

# 1. 按索引切割原生权重，保留11头对应的权重
c_attn_params_1_11 = slice_ordered_dict(c_attn_params, dim=-1, indices=head_1_11_indices)
# 2. 将切割后的权重加载到自定义Conv1D模块（c_attn_1_11）
model.q_attention.c_attn_1_11.load_state_dict(c_attn_params_1_11)

• slice_ordered_dict：自定义工具函数，按 dim=-1（权重矩阵的最后一维，对应 QKV 的维度）和之前生成的索引，切割原生 c_attn 的权重，得到适配 11 头的权重 c_attn_params_1_11。
• load_state_dict：PyTorch 加载权重的标准方法，将切割后的权重 “喂给” 自定义的 c_attn_1_11 模块（解决 Hugging Face 原生无此模块、无法自动加载权重的问题）。

步骤 5：返回适配后的量化模型

return model

• 最终返回 “加载了预训练权重 + 适配好 11 头 Conv1D 模块” 的 QGPT2LMHeadModel 实例，可直接用于后续量化推理或微调。

3. 核心解决的问题

Hugging Face 原生 GPT-2 的注意力层（c_attn）是为 12 个注意力头设计的，但自定义的量化注意力模块（q_attention）新增了 c_attn_1_11 模块（仅需 11 头）。

原生 from_pretrained 无法识别这个自定义模块，因此该方法通过手动提取、切割原生权重、再加载到自定义模块，实现了 “预训练权重复用” 与 “自定义量化模块适配” 的兼容。

class MultiHeadsAttention(QGPT2)

表示采用量化方法实现的多头机制的类

def run_numpy(self, q_inputs: np.ndarray) -> Union[np.ndarray, DualArray]:
        """运行将被转换为FHE的量化算子。
        该方法本质上是最初在Hugging Face的GPT2Attention模块的前向传播中实现的多头注意力机制，但仅使用量化算子。
        参数：
            q_inputs（np.ndarray）：量化输入。
        返回：
            Union[np.ndarray, DualArray]：量化输出。
        """

        # 使用存储的校准数据将输入转换为DualArray实例
        # q_x的形状为（n_batch，n_seq，n_embed）
        q_x = DualArray(float_array=self.x_calib, int_array=q_inputs, quantizer=self.quantizer)

        # 提取注意力基础模块名称
        mha_module_name = f"transformer.h.{self.layer}.attn."

        # 应用第一个投影以将Q、K和V提取为单个数组
        # q_qkv的形状为（n_batch，n_seq，3*n_embed）
        q_qkv = q_x.linear(
            weight=self.q_weights[mha_module_name + "c_attn.weight"],
            bias=self.q_weights[mha_module_name + "c_attn.bias"],
            key=f"attention_qkv_proj_layer_{self.layer}",
        )

        # 提取Q、K和V，其形状为（n_batch，n_seq，n_embed）
        q_q, q_k, q_v = q_qkv.enc_split(3, axis=-1, key=f"qkv_split_layer_{self.layer}")

        # 重塑Q、K和V，以便将它们拆分为12个注意力头，就像初始实现中所做的那样
        # q_q_mh、q_k_mh、q_v_mh的形状为（n_batch，n_head，n_seq，n_embed // n_head）
        splitted_head_shape = (
            q_x.shape[0],
            q_x.shape[1],
            self.config.n_head,
            q_x.shape[2] // self.config.n_head,
        )
        q_q_mh = q_q.reshape(
            splitted_head_shape, key=f"q_head_reshape_layer_{self.layer}"
        ).transpose((0, 2, 1, 3), key=f"q_head_transpose_layer_{self.layer}")
        q_k_mh = q_k.reshape(
            splitted_head_shape, key=f"k_head_reshape_layer_{self.layer}"
        ).transpose((0, 2, 1, 3), key=f"k_head_transpose_layer_{self.layer}")
        q_v_mh = q_v.reshape(
            splitted_head_shape, key=f"v_head_reshape_layer_{self.layer}"
        ).transpose((0, 2, 1, 3), key=f"v_head_transpose_layer_{self.layer}")

        # 计算注意力
        # q_y_mh 的形状为 (n_batch, n_head, n_seq, n_embed // n_head)
        q_y_mh = self.attention(q_q_mh, q_k_mh, q_v_mh)

        # 按照初始实现的方式，沿着轴-1合并回12个注意力头
        # q_y的形状为（n_batch, n_seq, n_embed）
        q_y_mh = q_y_mh.transpose((0, 2, 1, 3), key=f"head_transpose_layer_{self.layer}")
        q_y = q_y_mh.reshape(q_x.shape, key=f"head_reshape_layer_{self.layer}")

        # 为保证精度稳定性，将结果重新量化为n_bits位
        q_y = q_y.requant(key="q_y_requant")

        # 应用最后的投影
        # q_y的形状为（n_batch, n_seq, n_embed）
        q_y = q_y.linear(
            weight=self.q_weights[mha_module_name + "c_proj.weight"],
            bias=self.q_weights[mha_module_name + "c_proj.bias"],
            key=f"attention_last_proj_layer_{self.layer}",
        )

        return self.finalize(q_y)

该方法是量化版 GPT-2 多头注意力机制的核心执行函数，基于 NumPy 实现（无 PyTorch 依赖），核心目标是用 “量化算子” 复现 Hugging Face 原生 GPT2Attention 的前向逻辑，同时为后续转换为全同态加密（FHE）做准备，整体流程可拆解为 6 个关键步骤：

1. 输入量化转换：从数组到 DualArray

• 作用：将外部传入的量化整数数组（q_inputs），结合预先存储的 “校准浮点数数据”（self.x_calib）和量化器（self.quantizer），封装成自定义的DualArray对象。
• 意义：DualArray是量化框架的核心载体，同时保存 “浮点数参考值” 和 “量化整数实际值”，既支持量化计算，又能用于精度校准。
• 输入形状：(n_batch, n_seq, n_embed)（批量大小、序列长度、词向量维度）。

2. QKV 投影：单线性层提取查询 / 键 / 值

• 作用：通过 GPT-2 预训练的 “注意力投影层权重”（c_attn.weight）和偏置（c_attn.bias），对q_x做线性变换，一次性输出 “查询（Q）、键（K）、值（V）” 的合并数组。
• 关键细节：
  • 权重通过 “模块路径名”（mha_module_name = transformer.h.{层号}.attn.）精准定位，确保复用原生 GPT-2 的预训练参数；
  • 输出形状：(n_batch, n_seq, 3*n_embed)（3 倍词向量维度，对应 Q、K、V 各占 1 份）。

3. QKV 拆分与多头重塑

• 两步操作实现 “多头注意力” 的基础结构：

  1. 拆分 Q/K/V：用enc_split按最后一维（axis=-1）将合并数组拆分为 3 个独立数组， each 形状恢复为(n_batch, n_seq, n_embed)，分别对应 Q、K、V；

  2. 多头重塑与转置

     ：

     • 先将 Q/K/V 重塑为(n_batch, n_seq, n_head, n_embed//n_head)（n_head为注意力头数，如 GPT-2 默认 12 头，每头维度 = 词向量维度 / 12）；
     • 再通过transpose调整维度顺序为(n_batch, n_head, n_seq, n_embed//n_head)，目的是让 “每个注意力头” 能独立计算（维度顺序适配后续注意力分数计算）。

4. 多头注意力计算

• 作用：调用自定义的注意力计算逻辑（self.attention），输入重塑后的 Q/K/V（q_q_mh/q_k_mh/q_v_mh），输出每个头的注意力结果。
• 输出形状：与输入一致，仍为(n_batch, n_head, n_seq, n_embed//n_head)（每个头对应一组序列级的注意力输出）。
• 隐藏逻辑：内部会复现原生 GPT-2 的注意力计算（如缩放点积、掩码、SoftMax、加权求和），但全程用量化算子执行。

5. 多头结果合并与重量化

• 两步操作还原单头维度：
  1. 多头合并：先通过transpose将维度顺序转回(n_batch, n_seq, n_head, n_embed//n_head)，再用reshape合并 “多头维度”，最终恢复为(n_batch, n_seq, n_embed)（与输入q_x形状一致）；
  2. 重量化：调用requant将合并后的结果重新量化到n_bits（预设量化位数），目的是保证经过多步计算后的数值精度稳定，避免量化误差累积。

6. 最终投影与输出

• 作用：通过 GPT-2 预训练的 “注意力输出投影层”（c_proj.weight/c_proj.bias），对合并后的注意力结果做最后一次线性变换，完成整个注意力模块的计算。
• 输出处理：调用self.finalize(q_y)对结果做收尾（如根据 FHE 模式决定输出np.ndarray还是DualArray），最终返回量化输出。

核心设计目标

1. 功能对齐：1:1 复现原生 GPT-2 多头注意力的前向逻辑，确保量化后模型效果不偏离预训练性能；
2. 量化兼容：全程使用DualArray和量化算子，避免浮点数计算，适配 FHE 对 “整数运算” 的要求；
3. 参数复用：直接调用原生 GPT-2 的预训练权重（c_attn/c_proj），无需额外训练量化模型。

class QGPT2MultiHeadsAttention(QGPT2Attention):
    """一个Torch模块，它用量化操作重写了GPT-2的多头注意力机制。"""

    def __init__(self, config, layer, n_bits=16):
        super().__init__(config)

        # 实例化用于多头注意力机制的量化模块
        self.q_module = MultiHeadsAttention(n_bits=n_bits, layer=layer)

    def forward(
        self,
        hidden_states: Optional[Tuple[torch.FloatTensor]],
        layer_past: Optional[Tuple[torch.Tensor]] = None,
        attention_mask: Optional[torch.FloatTensor] = None,
        head_mask: Optional[torch.FloatTensor] = None,
        encoder_hidden_states: Optional[torch.Tensor] = None,
        encoder_attention_mask: Optional[torch.FloatTensor] = None,
        use_cache: Optional[bool] = False,
        output_attentions: Optional[bool] = False,
    ) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:
        """GPT-2的多头注意力传递是为FHE计算设计的。
        初始实现可在huggingFace的GPT2Attention类中找到。
        """
        if encoder_hidden_states is not None:
            raise ValueError(
                "Class cannot be used as cross attention, please make sure to not instantiate "
                "class with `GPT2Attention(..., is_cross_attention=True)`."
            )

        if self.reorder_and_upcast_attn:
            raise ValueError("Method 'reorder_and_upcast_attn' is not implemented")

        #使用符合FHE的运算符应用多头注意力机制
        attn_output = self.q_module.run_torch(
            hidden_states,
            fhe=self.fhe,
            true_float=self.true_float,
        )

        # 该方法不处理缓存选项
        return (attn_output, None)

该类是基于 QGPT2Attention（继承自 Hugging Face 的 GPT2Attention）实现的量化版 GPT-2 多头注意力模块，核心目标是在保留多头注意力逻辑的同时，集成量化操作以适配全同态加密（FHE）计算场景，解决 FHE 对 “低精度、特定运算符” 的依赖问题。

1. 类的核心定位

• 继承关系：QGPT2MultiHeadsAttention → QGPT2Attention → GPT2Attention，本质是对原生 GPT-2 多头注意力的 “量化改造”，而非从零实现。
• 核心功能：用自定义的量化模块（MultiHeadsAttention）替代原生注意力的计算逻辑，确保前向传播过程符合 FHE 计算要求（如低精度运算、兼容 FHE 运算符）。

2. init 初始化方法

作用

完成量化模块的实例化，为后续注意力计算准备量化能力。

关键逻辑

• 调用父类初始化：super().__init__(config) 继承 QGPT2Attention 的基础配置（如 FHE 模式开关 self.fhe、浮点数计算开关 self.true_float）。

• 实例化量化核心

  ：

  self.q_module = MultiHeadsAttention(n_bits=n_bits, layer=layer)
  

  • n_bits：量化位数（默认 16 位，可控制量化精度，位数越低越适配 FHE，但可能损失模型性能）；
  • layer：当前注意力层的索引（用于定位模型权重、区分不同层的量化参数）；
  • self.q_module 是实际执行 “量化 + 多头注意力计算” 的核心模块，封装了量化逻辑（如权重 / 激活值的量化 / 反量化、符合 FHE 的运算符）。

3. forward 前向传播方法

作用

定义量化版多头注意力的计算流程，输出注意力层的结果（适配 FHE 模式）。

关键逻辑拆解

（1）输入合法性校验

• 禁止交叉注意力：通过 if encoder_hidden_states is not None 抛出错误，说明该类仅支持 “自注意力”（GPT-2 decoder 核心逻辑），不支持跨模态 / 跨序列的交叉注意力。
• 禁止重排序与上采样：通过 if self.reorder_and_upcast_attn 抛出错误，说明该类未实现原生 GPT2Attention 中的 “注意力重排序 + 精度上采样” 逻辑（因 FHE 需简化运算，暂不支持）。

（2）量化注意力计算

核心代码：attn_output = self.q_module.run_torch(...)

• 调用self.q_module（量化多头注意力模块）的run_torch方法，传入 3 个关键参数：
  1. hidden_states：当前层的输入特征（需量化处理的核心数据）；
  2. fhe=self.fhe：FHE 模式（继承自 QGPT2Attention，可选 disable 禁用 /simulate 模拟 /execute 实际执行）；
  3. true_float=self.true_float：是否用浮点数计算（仅 fhe=disable 时生效，用于对比 “量化” 与 “非量化” 的性能差异）。
• 该方法内部会完成：输入量化 → 量化多头注意力计算 → 输出反量化，最终得到 attn_output（注意力层输出特征）。

（3）输出结果

• 返回(attn_output, None)：
  • 第一个元素 attn_output：注意力层的计算结果；
  • 第二个元素 None：因代码注释 “不处理缓存选项”（use_cache 参数未实际使用），故缓存相关结果设为 None，与原生 GPT2Attention 的输出格式（(attn_output, present)）兼容。

4. 核心设计目的

1. 适配 FHE：通过量化（降低数据精度）和简化运算（移除不兼容 FHE 的逻辑），让 GPT-2 的多头注意力可在 FHE 环境中运行（保护数据隐私，无需解密计算）；
2. 兼容性：继承自原生 GPT2Attention，输出格式与原生一致，可无缝替换原生注意力层，无需修改模型其他部分；
3. 可调试性：支持 fhe=simulate（模拟 FHE 计算）和 true_float=True（浮点数计算），方便对比不同模式下的模型效果与性能。

class MultiHeadsQGPT2Model(QGPT2LMHeadModel)

具有多头注意力机制且可在FHE中执行的QGPT2LMHeadModel实现。

def __init__(self, config: GPT2Config, n_bits: int = 16, layer: int = 0):
        super().__init__(
            config, n_bits=n_bits, attention_module=QGPT2MultiHeadsAttention, layer=layer
        )

1. 方法定义与参数

   • def __init__(self, config: GPT2Config, n_bits: int = 16, layer: int = 0)
     

     • self：类实例的引用（必选参数），用于访问实例的属性 / 方法；
     • config: GPT2Config：必选参数，传入 GPT-2 模型的配置对象（如模型层数、隐藏层维度等核心参数），类型标注确保传入参数符合GPT2Config类规范；
     • n_bits: int = 16：可选参数，量化位数（默认 16 位），用于指定模型量化时的精度（如 16 位量化、8 位量化等，影响模型大小和推理速度）；
     • layer: int = 0：可选参数，目标层索引（默认第 0 层），指定要对 GPT-2 模型的哪一层进行量化改造。

2. 核心逻辑：调用父类构造

   • super().__init__(config, n_bits=n_bits, attention_module=QGPT2MultiHeadsAttention, layer=layer)
     

     • super()：获取当前类的父类（结合背景代码，父类应为QGPT2LMHeadModel）；
     • 调用父类的__init__方法，将当前方法的参数传递给父类，同时固定传入量化注意力模块QGPT2MultiHeadsAttention—— 即该类实例化时，会自动用 “多头量化注意力模块” 改造 GPT-2 指定层，无需外部手动传入注意力模块类型，简化了使用流程。