欧拉路径的判断(并查集,DFS)
题目

我的题解
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
map<int, int>mp;
int n, m;
cin >> n >> m;
for (int i = 1;i < n+1;i++) {
mp.insert(pair<int, int>(i, 0));
}
for (map<int, int>::iterator it = mp.begin();it != mp.end();it++) {
//cout << it->first << " " << it->second << endl;
}
int a[10][2];
for (int i = 0;i < m;i++) {
for (int j = 0;j < 2;j++) {
cin >> a[i][j];
}
int key1 = a[i][0];
int key2 = a[i][1];
map<int, int>::iterator it1 = mp.find(key1);
it1->second++;
map<int, int>::iterator it2 = mp.find(key2);
it2->second--;
}
int count1 = 0;
int count2 = 0;
for (map<int, int>::iterator it = mp.begin();it != mp.find(n+1);it++) {
//cout << it->first << " " << it->second<<endl;
if (it->second <= -1)count1++;
if (it->second >= 1)count2++;
}
//cout << count1 << count2 << endl;
if ((count1 == 1) && (count2 == 1)) {
cout << "Yes";
}
else {
cout << "No";
}
return 0;
}
问题
没有考虑没有连通的情况
正确思路
1.先判断是否连通,即连通分支数为1(可以用并查集或dfs)
2.只有一个结点入度为1,一个结点出度为1,其余结点出度=入度
并查集
定义
把连通的两个点合并,如果最后只有一个集合,那么该图连通,否则不连通。
实现
并查集由一个整数型的数组和两个函数构成。数组pre[]记录了每个点的前导点是什么,函数find是查找,join是合并。
数组下标是当前点的号码,值是前导点的号码,如果值和下标一样代表自己是根。
查找是找根用的,直到找到值和下标一样的根位置
合并就是在两个根之间修改其中一个根的值为另一个根的下标或者值。
路径压缩算法:最理想的情况就是所有点的前导点都是相同的根,一共就是两级结构。做法就是在查找时找到根之后把自身的值修改成根的下标。
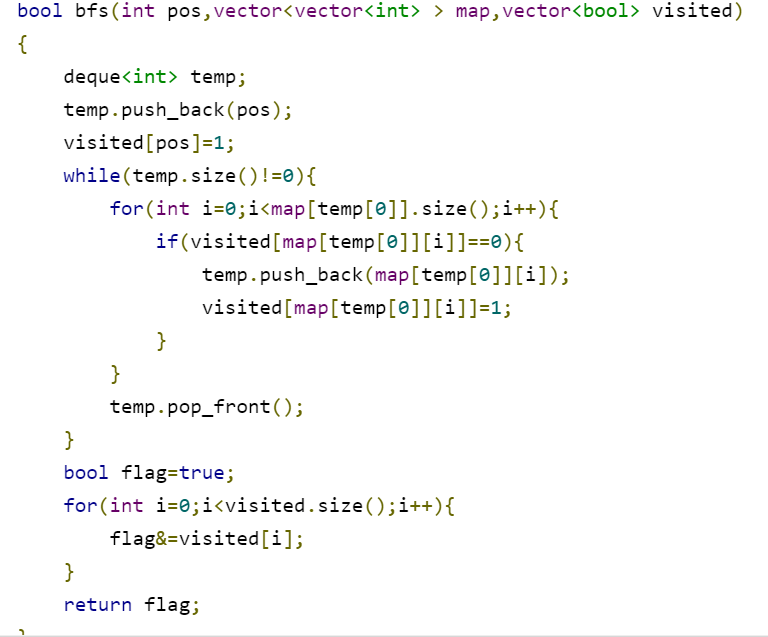
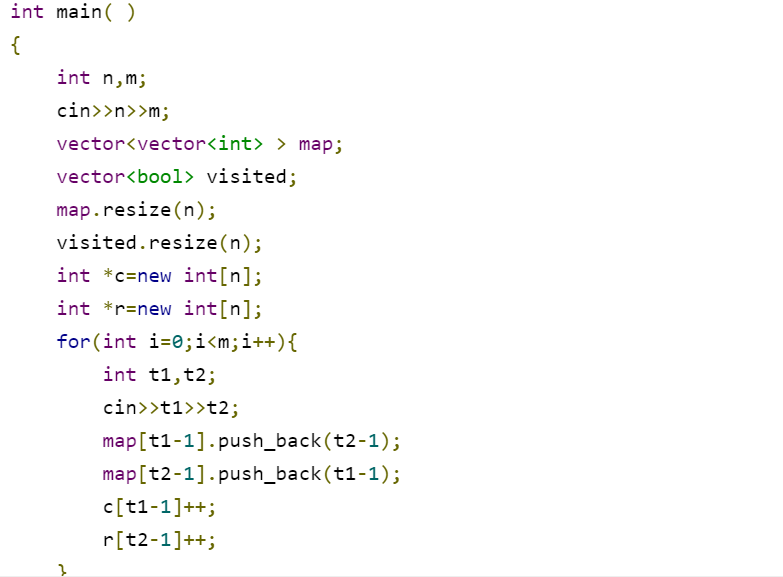
正确代码






 浙公网安备 33010602011771号
浙公网安备 33010602011771号