人工智能必备数学知识01

 

1. 高等数学基础

函数的定义

• 量和量之间的关系如：A = π r²  ；
• y = f(x) 其中x是自变量，y是因变量；
• 函数在x₀处取得的函数值y₀ = y|_x=x0 = f(x₀)
• 符号只是一种表示，也可以 y = g(x)等

几种函数

分段函数： 

 

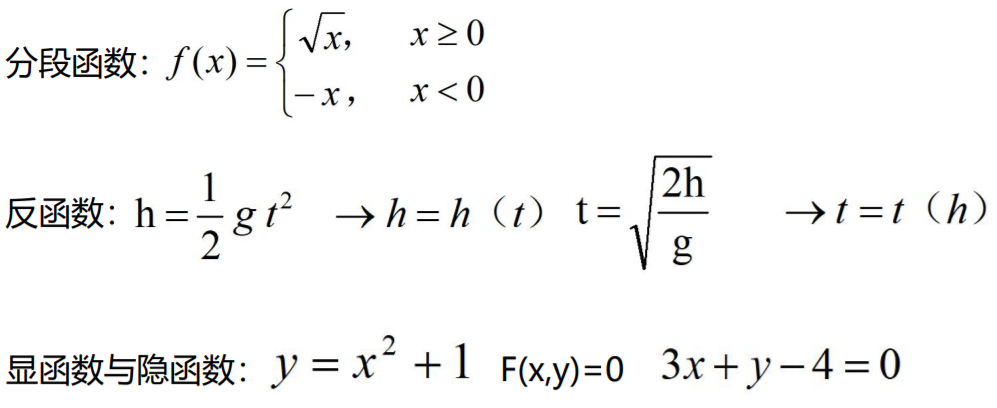
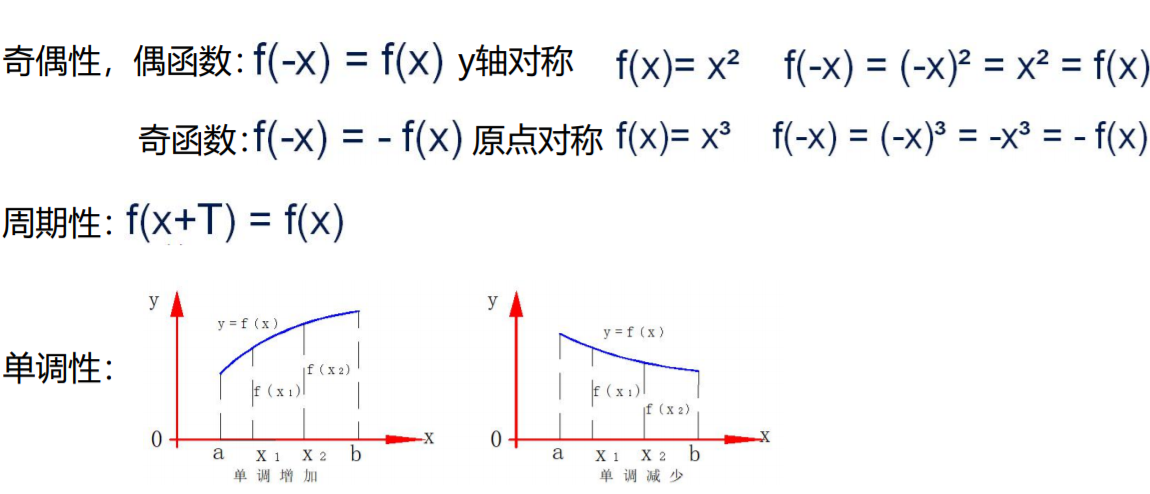
 几种特性

数列

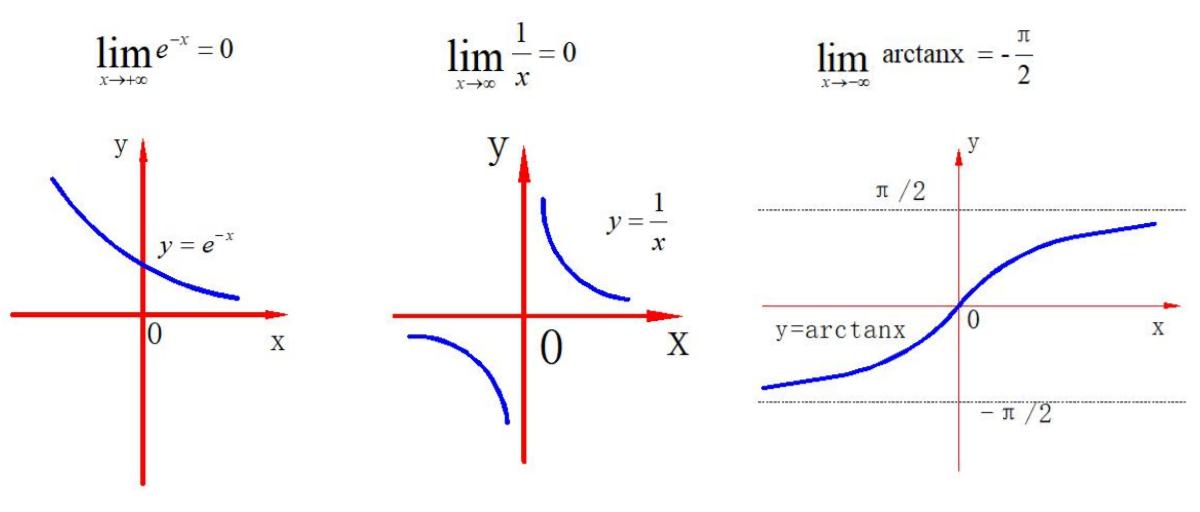
极限

 

 

 

 

 

 

 

函数的连续型

 

 

 

 

 

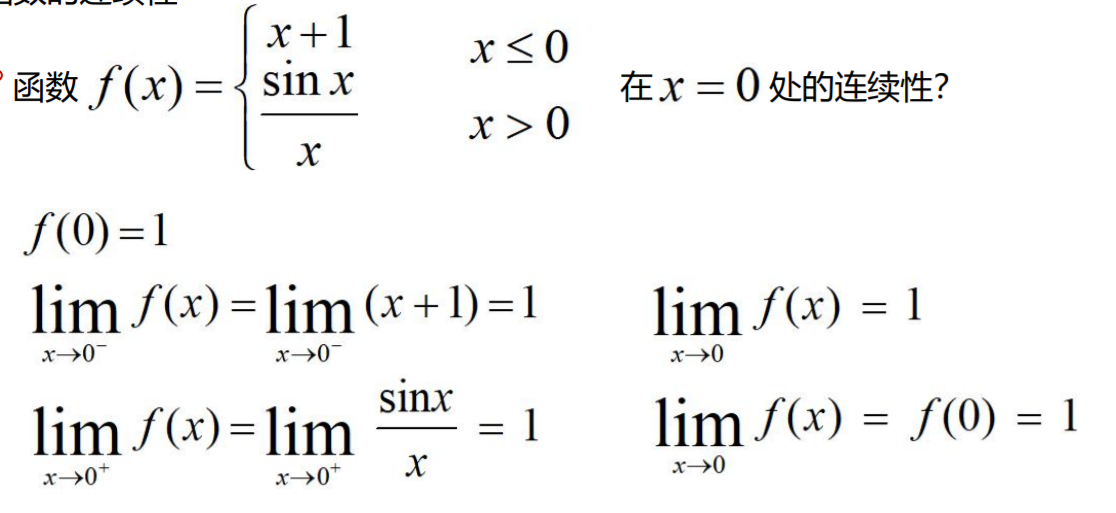
 导数

 

 

 

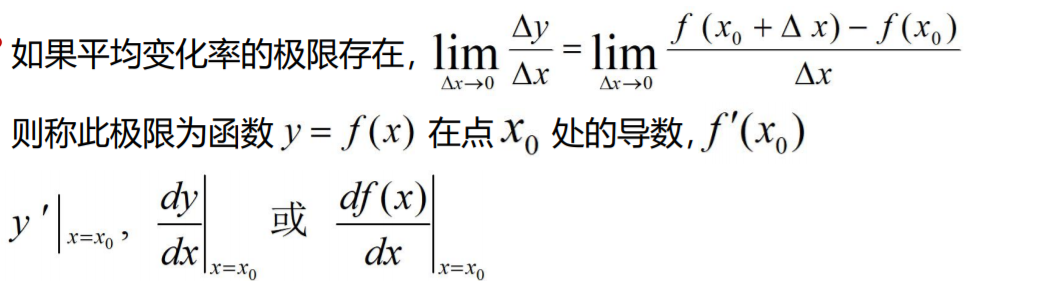
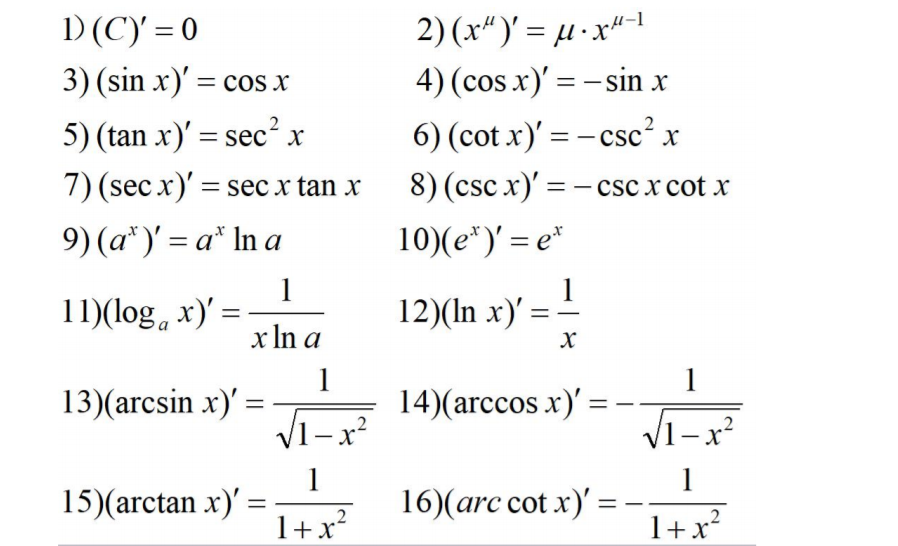
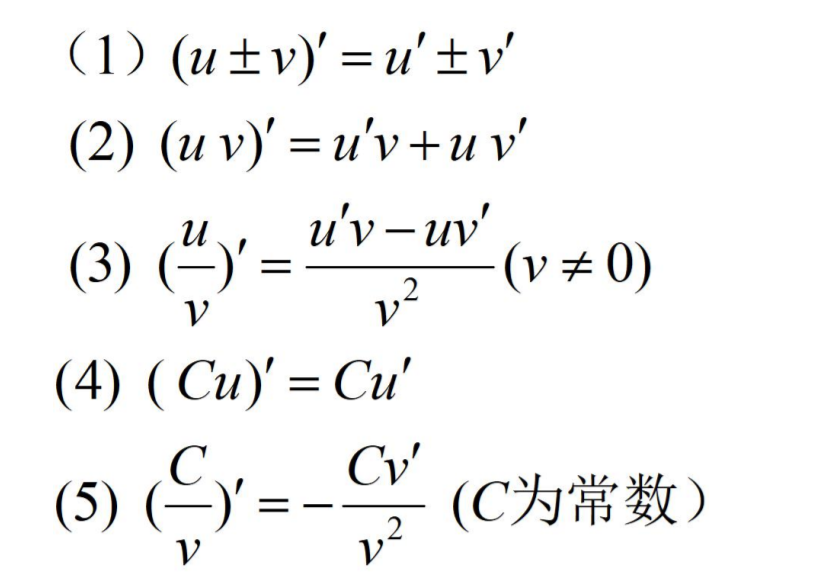
梯度

偏导数

对于一元函数y=f(x)只存在y随x的变化率

二元函数z=f(x,y)存在z随x变化的变化率，随y变化的变化率，随x﹑y同时变化的变化率。

 

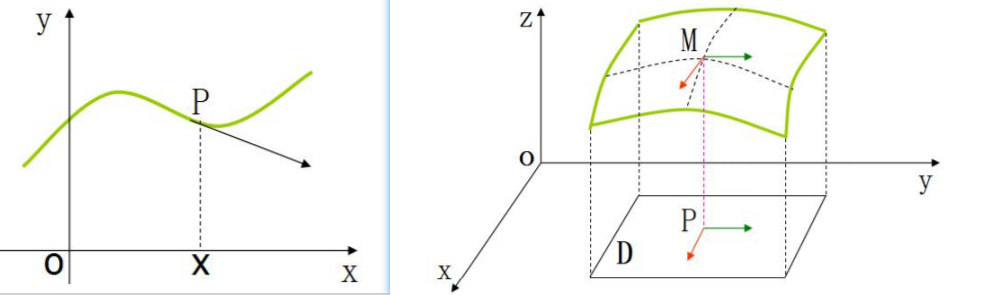
偏导数

定义：设函数z = f(x, y) 在点(x₀, y₀) 的某个邻域内有定义, 定y = y₀ ，一元函数f(x, y₀) 在点x = x₀ 处可导，即极限

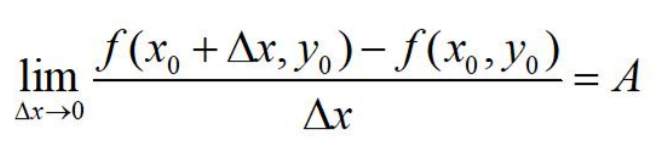
则称 A为函数：z = f(x, y) 在点(x₀, y₀) 处关于自变量X的偏导数 

记作：f_x(x₀, y₀)  或者 

 

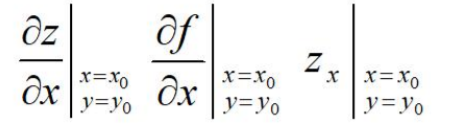
 求f(x, y) = x² + 3xy + y² 在点(1, 2) 处的偏导数：

  f_x(x, y) = 2x + 3y = f_x(1, 2) = (2x + 3y) | _{x=1, y=2} = 8 

  f_y(x, y) = 3x + 2y = f_y(1, 2) = (3x + 2y) | _{x=1, y=2} = 7

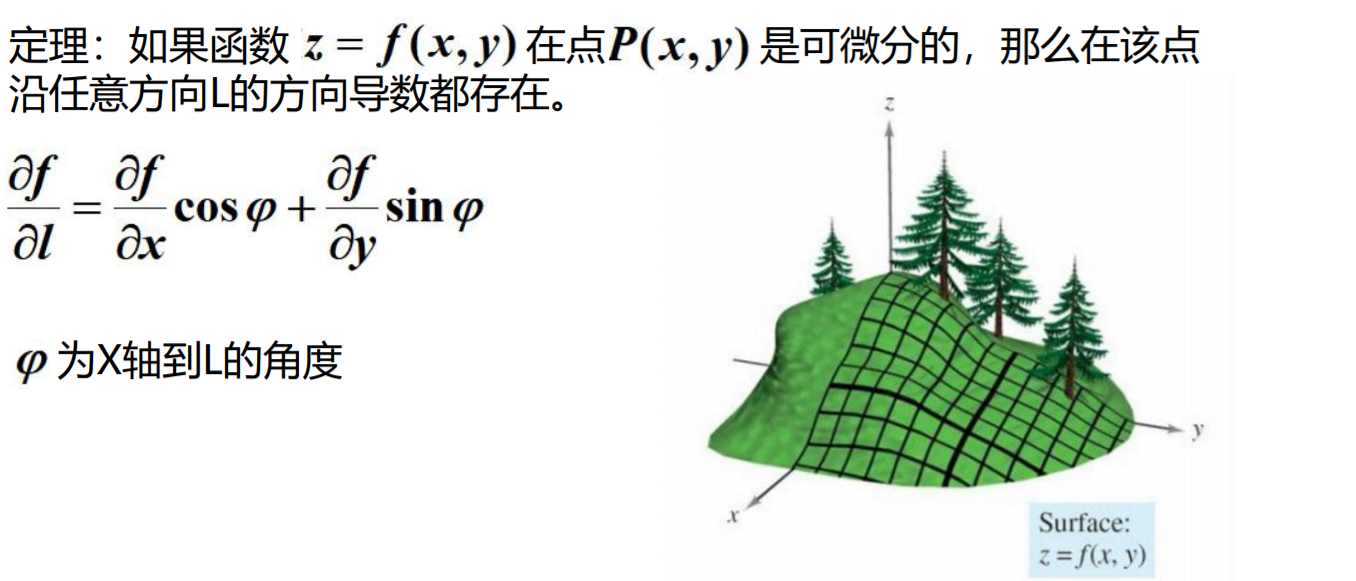
方向导数

蚂蚁沿着什么方向跑路才能活？ 

函数：z = f(x, y) 

 

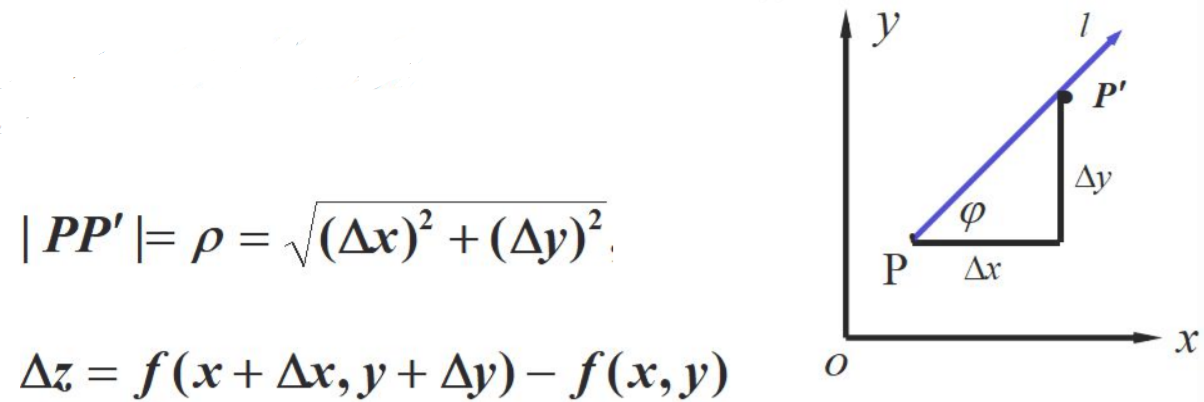
方向导数

如果函数的增量，与这两点距离的比例存在，则称此为在P点沿着L的方向导数

 

 

 

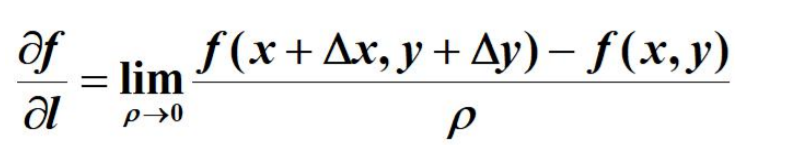
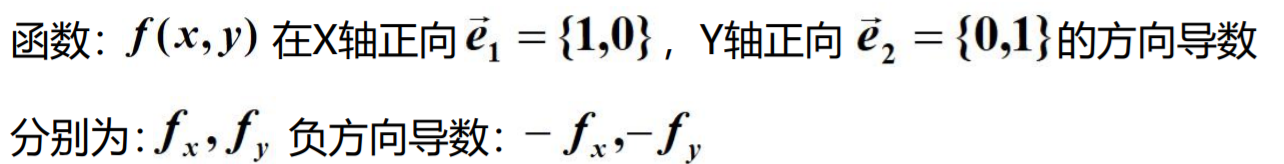
 梯度

 

 

 

2. 微积分

起源：微积分诞生于17世纪，主要帮助人们解决各种速度问题，面积等实际问题；

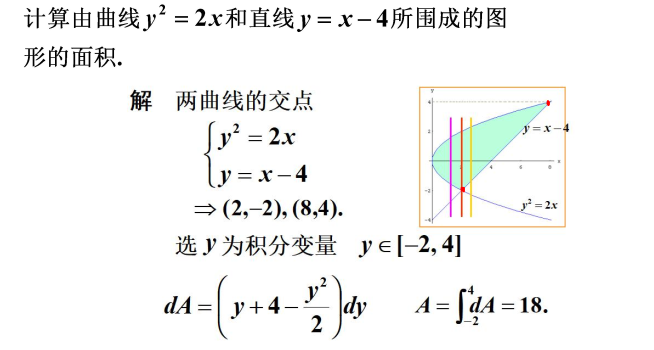
如何求曲线的面积呢？

以直代曲

• 对于矩阵，我们可以轻松求得其面积，能否用矩形代替曲线形状呢？
• 应该用多少个矩阵来代替呢？

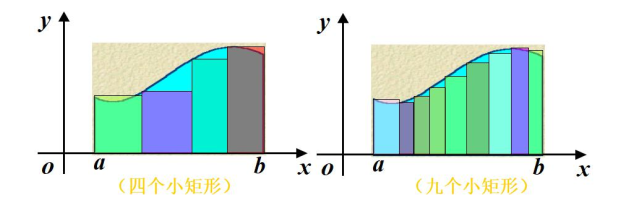
 面积由来

 从求和出发

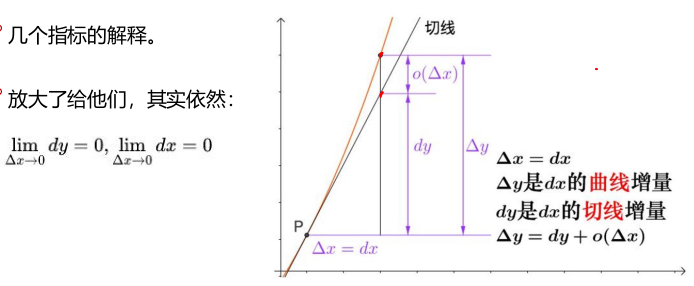
 切线的解释

 微分是什么

 定积分

 

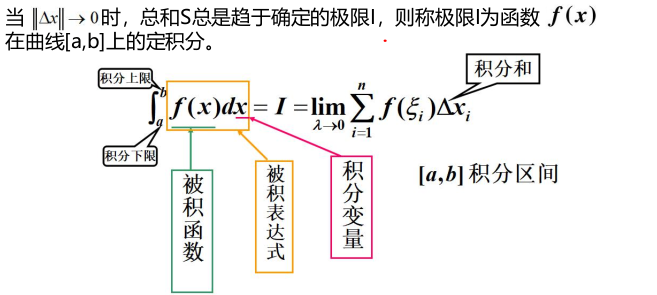
定积分的几何意义

 

 

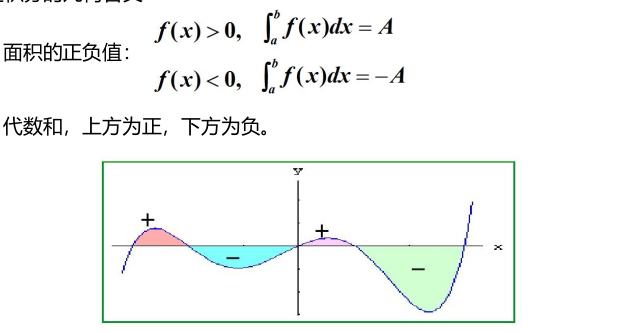
 定积分的性质

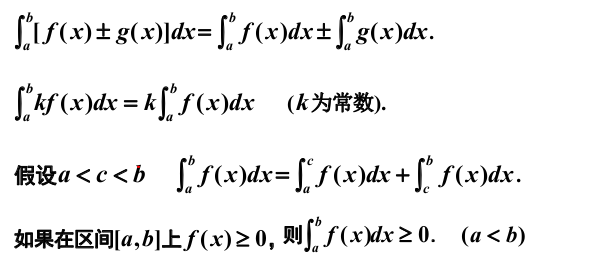
 第一中值定理

 积分上限函数

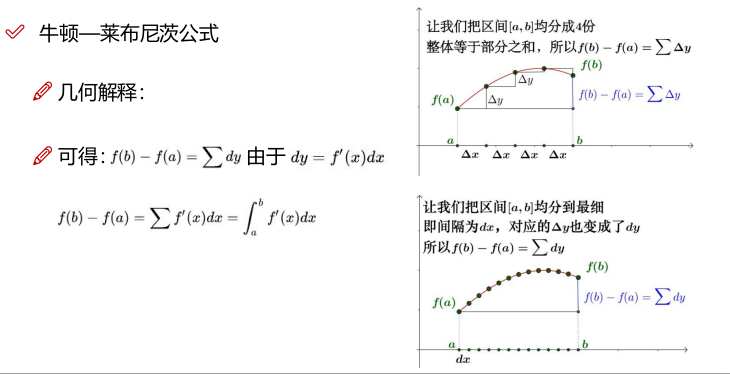
 牛顿-莱不尼茨公式

 

 

 

 

3. 泰勒公式与拉格朗日

拉格朗日

如何求极值？

• 给个函数：z = f(x, y) 如何求其极值点呢？
• 简单来说直接求它的偏导不就OK啦嘛，f_x(x, y) = 0，f_y(x, y) = 0
• 现在问题难度加大了，如果再加约束条件呢? 面积固定，求体积最大 = ? 
  • V(x, y, z) = xyz 
  • 2xy + 2yz + 2zx = S

什么点是我们想要的？

山峰的高度是f(x, y)，其中有一条曲线是g(x, y) = C

曲线镶嵌在山上，如何找到曲线最低点呢？

法向量平行：▽f(x, y) = -λ ▽g(x, y) 

得到结论： ▽( f(x, y) + λg(x, y) ) = 0

 

 自变量多于两个条件下

 实例

 

 

 

 

 

 

泰勒公式

出发点

• 用简单的熟悉的多项式来近似代替复杂的函数
• 易计算函数值，导数与积分仍是多项式
• 多项式由它的系数完全确定，其系数又由它在一点的函数值及其导数所确定。

微分：

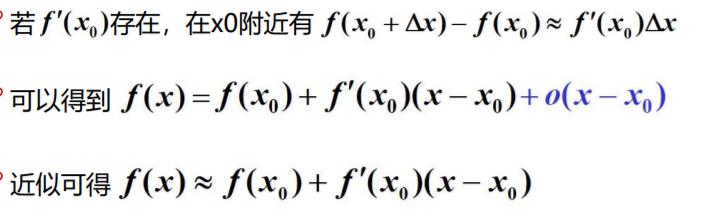
 以直代曲

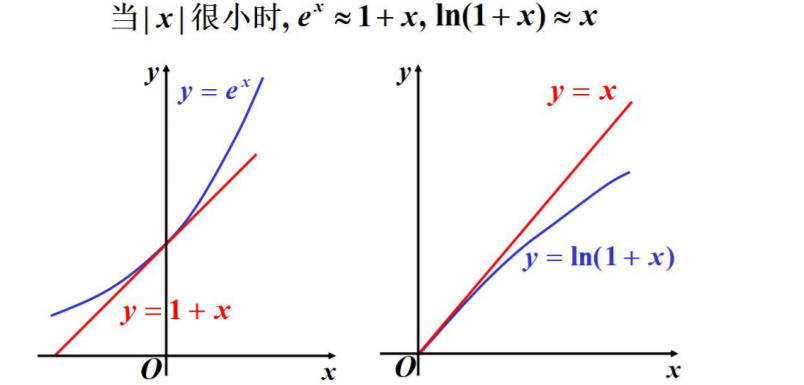
 一点一世界 

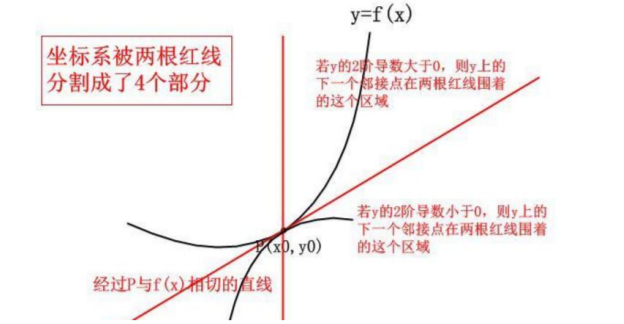
　　只用一阶导看起来有点不准，能不能再利用一些？

 　　一阶导只能帮我们定位下一个点是上升还是下降，对之后的趋势就很难把控了；

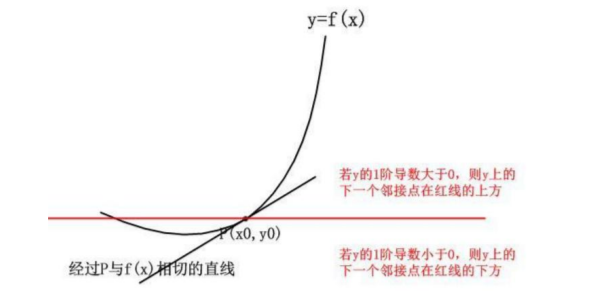
 　　如何做的更准确些，把二阶段利用上呢？

 

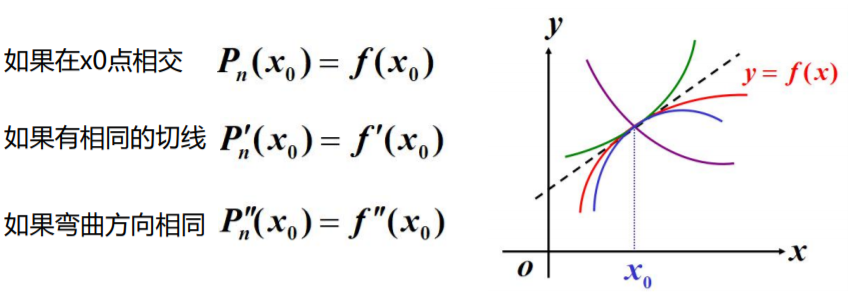
泰勒多项式

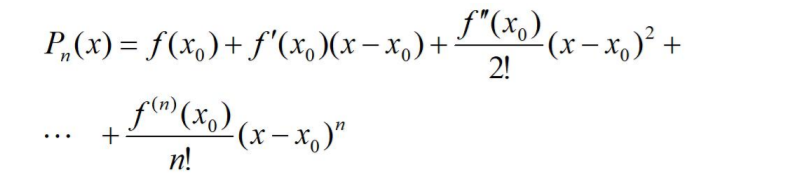
 称f(x)的在x0关于(x - x0) 的n阶泰勒多项式 ；

麦克劳林公式

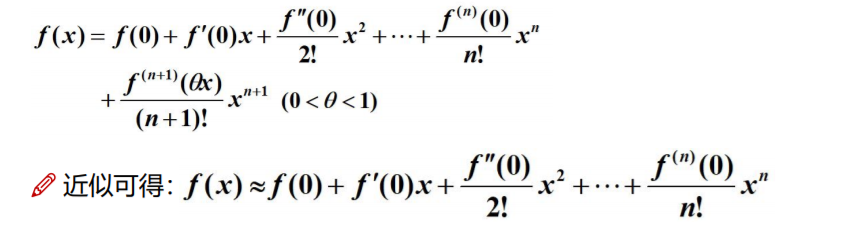
多项式逼近

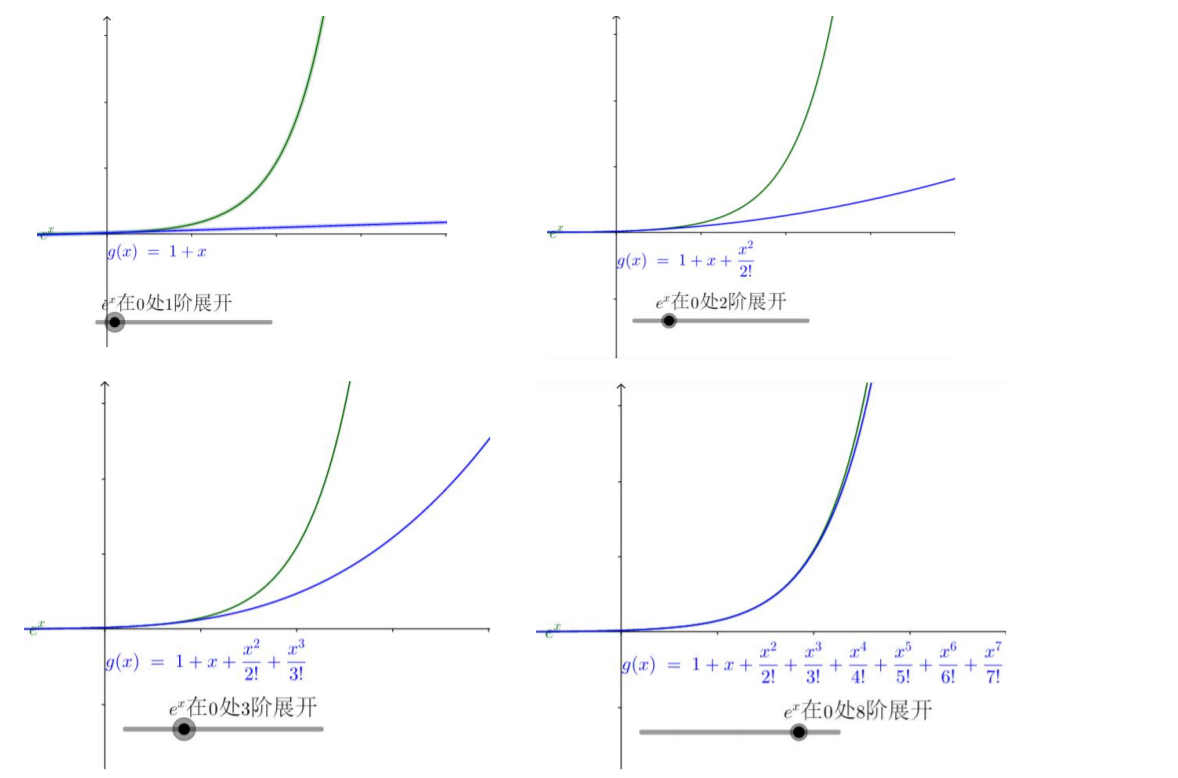
 阶数是什么意思？

• 阶数越高增长速度越快；
• 观察可发现，越高次项在越偏右侧影响越大；
• 对于一个复杂函数，给我们的感觉是在当前点，低阶项能更好的描述当前点附近，对于之后的走势就越来越依靠高阶的了；

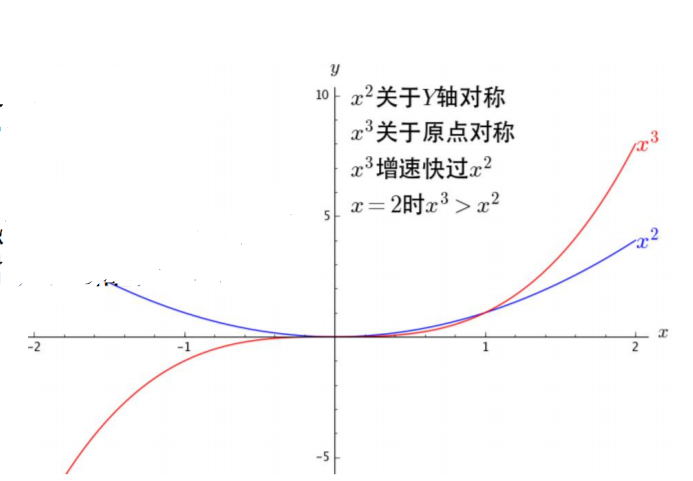
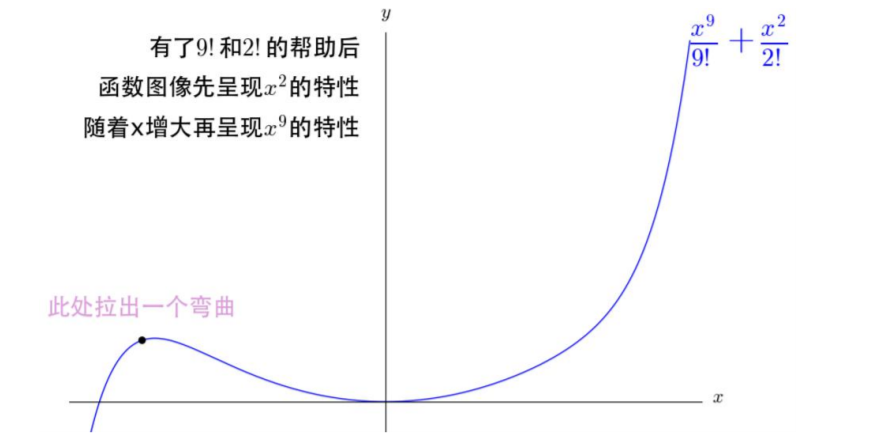
如果把9次的和2次的直接放在一起，那2次的就不用玩了；

但是在开始的时候应该是2次的效果更好，之后才是慢慢轮到9次的呀！

 

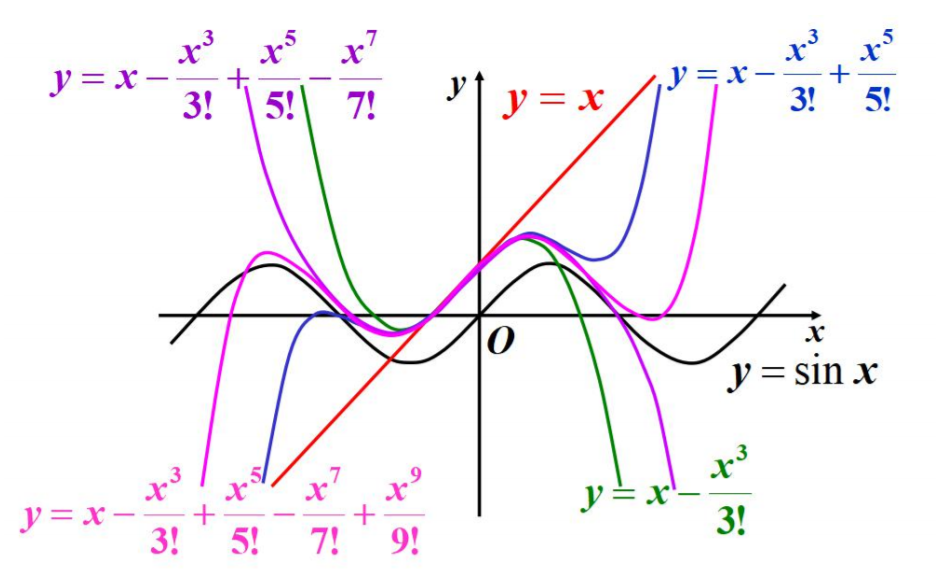
 多项式逼近

逼近sinx 

 

 

4. 线性代数基础 

行列式

二元线性方程组的求解

• a₁₁ x₁ + a₁₂ x₂ = b₁ 
• a₂₁ x₁ + a₂₂ x₂ = b₂ 

(a₁₁ a₂₂  - a₁₂ a₂₁ ) x₁ = b₁ a₂₂ - a₁₂b₂ 

(a₁₁ a₂₂  - a₁₂ a₂₁ ) x₂ = a₁₁b₂  - b₁a₂₁ 

当a₁₁ a₂₂  - a₁₂ a₂₁  ！= 0 方程组有唯一解：

•  x₁  = (b₁ a₂₂ - a₁₂b₂) / (a₁₁ a₂₂  - a₁₂ a₂₁ ) 
•  x₂  = ( a₁₁b₂  - b₁a₂₁ ) / (a₁₁ a₂₂  - a₁₂ a₂₁ )

看起来好像有些规律

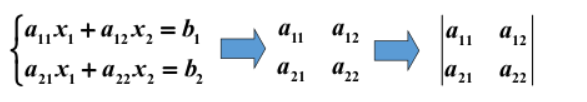
 表达式 a₁₁ a₂₂  - a₁₂ a₂₁ 即为二阶行列式

 三阶行列式

二阶看起来挺容易就算出来了，三阶的呢？

 

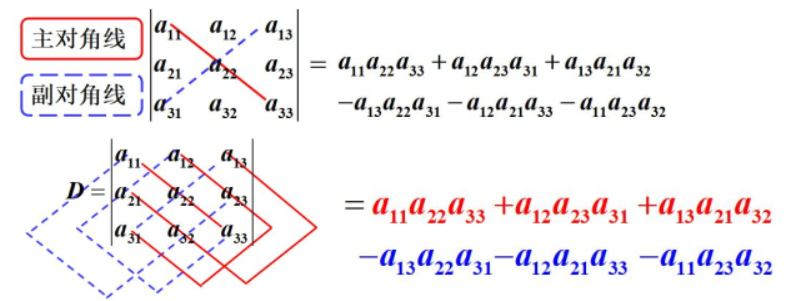
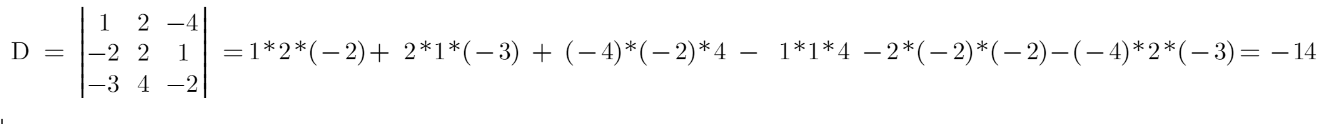
矩阵

矩阵和数据之间的关系

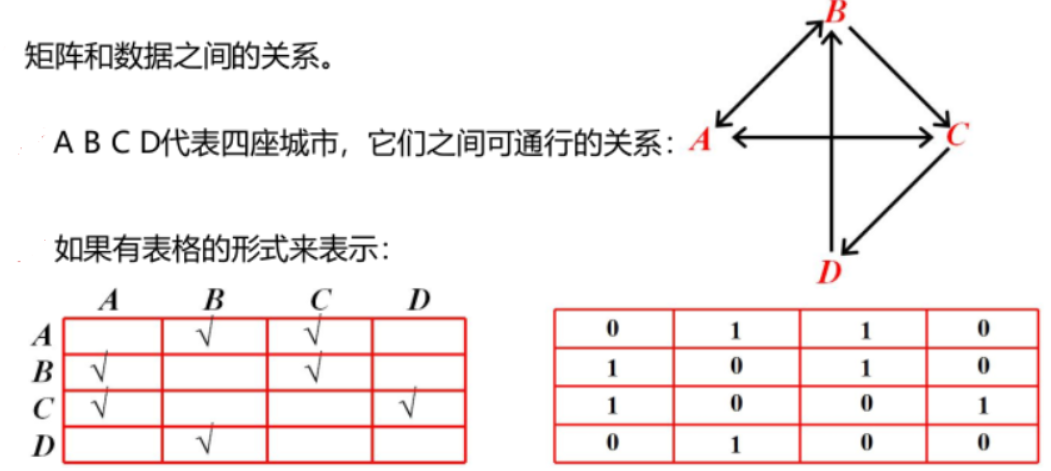
行列式与矩阵的区别 

                   

何为矩阵 

输入的数据就是矩阵，对数据做任何的操作都是矩阵的操作了；

 

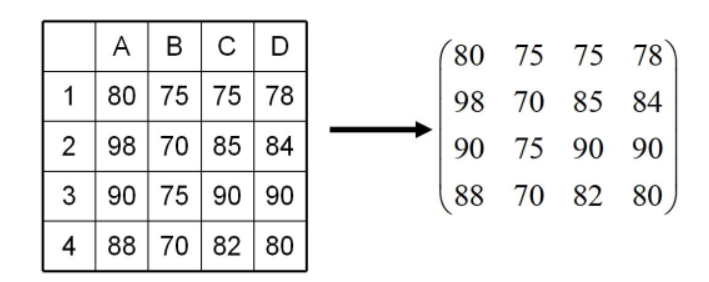
 方阵是什么？

　　行和列一样就是方阵啦，一般叫做n阶方阵；

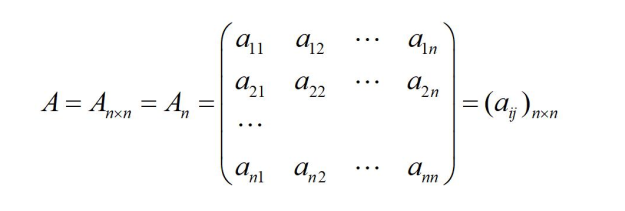
几种特别的矩阵

 

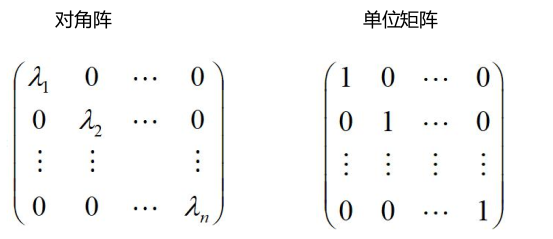
 同型矩阵和矩阵相等是一个事吗？

 

矩阵基本运算

加减法

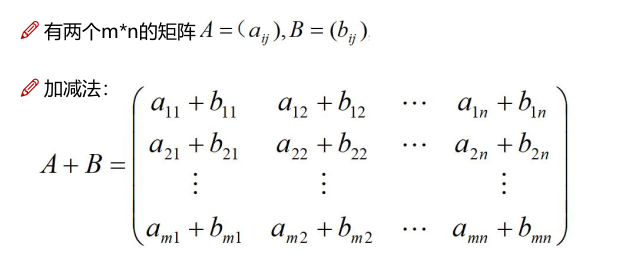
 数乘运算，数 与矩阵A的乘积 

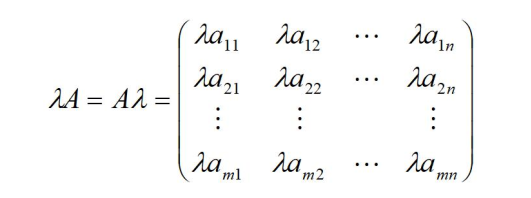
 矩阵的乘法

两个商场，三种电视机，求销售额？（A的列数与B的行数要相等）

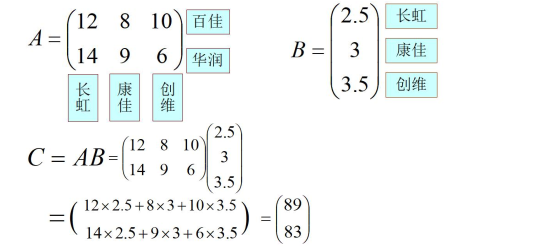
 乘法没有交换律

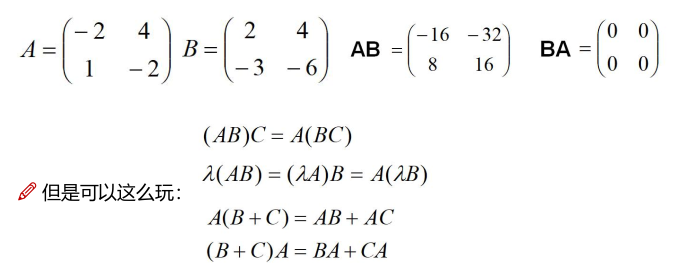
方程呢，A为系数矩阵，X是未知数矩阵，B是常数矩阵。 

 

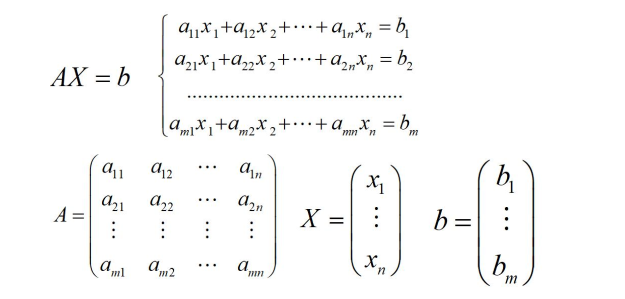
 矩阵转置

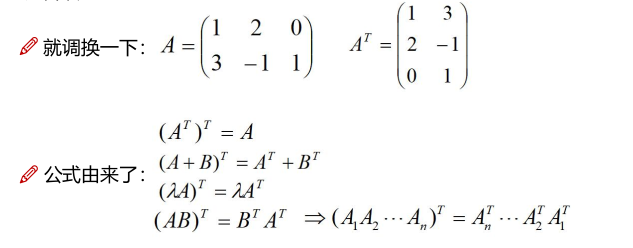
对称矩阵

如果满足A^T = A ，那么A就是对阵矩阵；

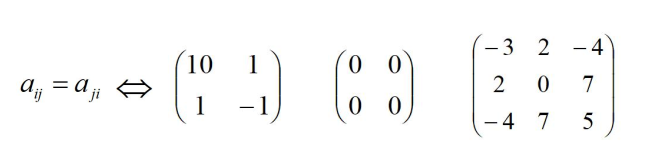
 逆矩阵

　　A为n阶方阵，如果存在n阶方阵B，使得AB = BA = I (单位阵)，记作：B = A^-1

 

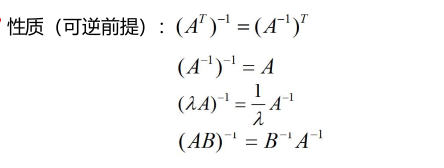
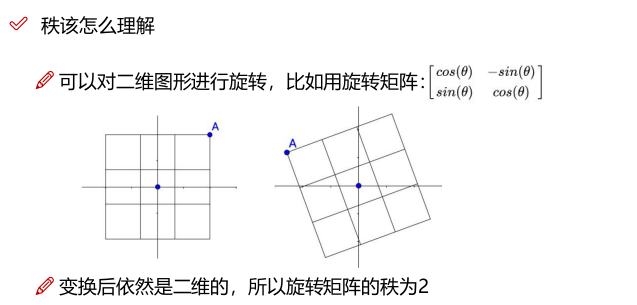
矩阵的秩

 

 

 

 

 

 

 

 

 

 

 

 

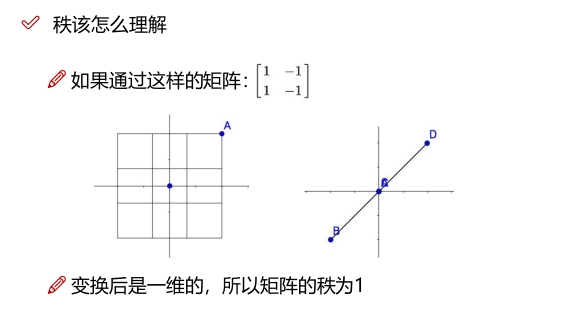
5. 特征值与矩阵分解

特征值

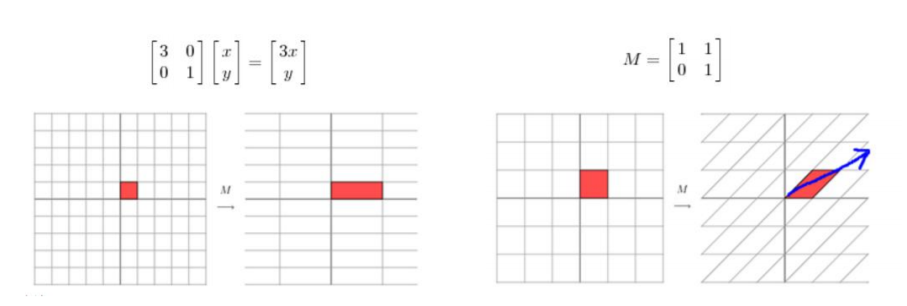
矩阵究竟做了什么

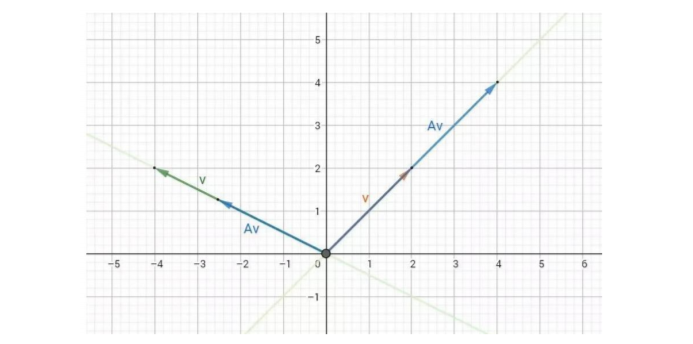
矩阵对向量可以做拉伸也可以做旋转

特征值和特征向量描述了什么

拳击怎么赢？攻击的方向和力量！

我们可以把方向当做是特征向量，在这个方向上用了多大力量就是特征值。

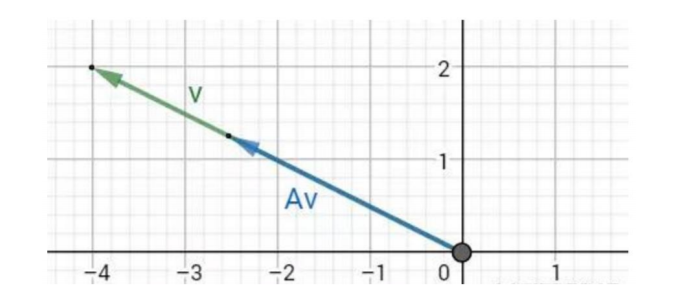
数学定义：

对于给定矩阵A，寻找一个常数λ 和非零向量x，使得向量x 被矩阵A作用后所得的向量Ax 与原向量x 平行，并且满足Ax = λx 

特征空间

特征空间中包含了所有的特征向量

特征向量的应用

既然特征值表达了重要程度且和特征向量所对应，那么特征值大的就是主要信息了，基于这点我们可以提取各种有价值的信息了。 

SVD矩阵分解

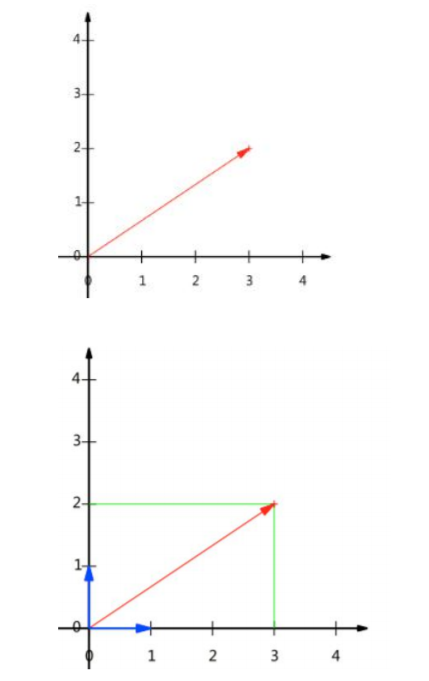
向量的表示及基变换 

向量可以表示为(3,2)， 实际上表示线性组合：x(1, 0)^T + y(0, 1)^T 

基：(1,0)和(0,1)叫做二维空间中的一组基

 

基变换

　　基是正交的（即内积为0，或直观说相互垂直）

　　要求：线性无关

 

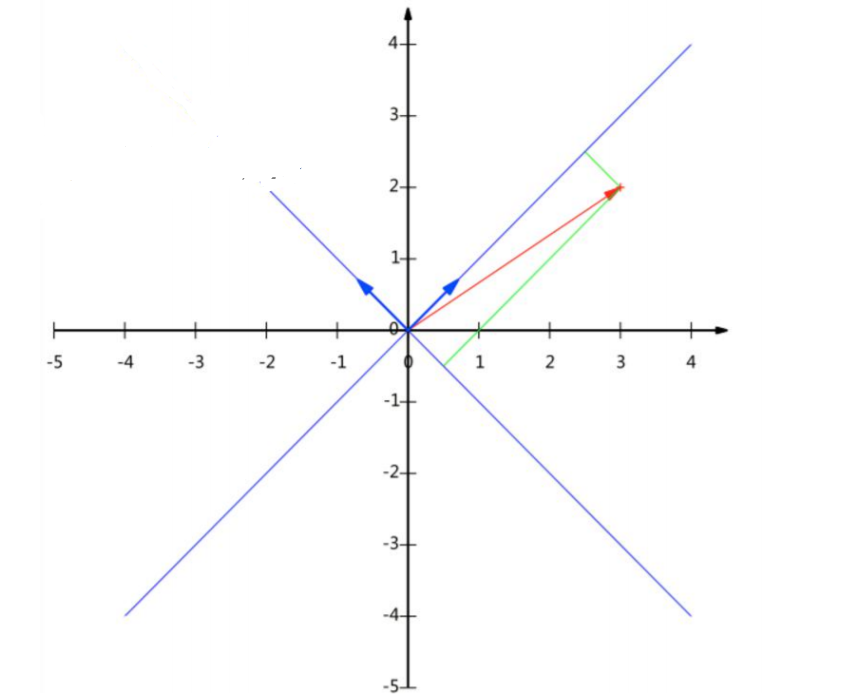
变换：数据与一个基做内积运算，结果作为第一个新的坐标分量，然后与第二个基做内积运算，结果作为第二个新坐标的分量

数据（3，2）映射到基中坐标：

                                         

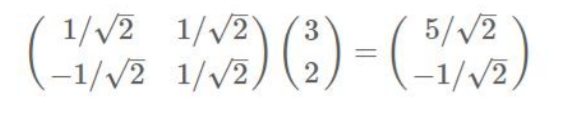
 矩阵乘以一个向量, 结果仍是一个向量

 

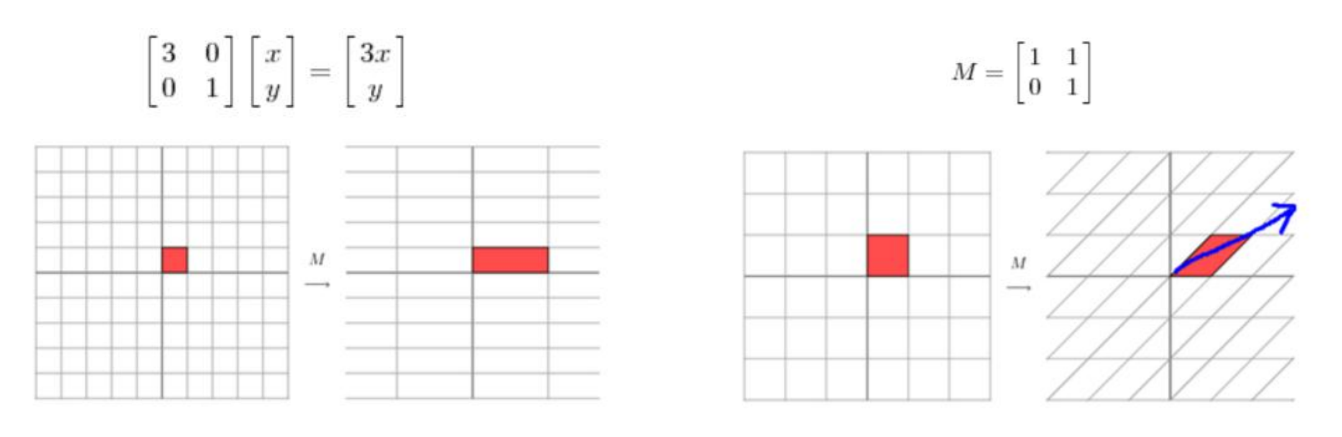
特征值分解

矩阵里面的信息有很多呀？来分一分吧！A = UΛU^-1 

当矩阵是N*N的方阵且有N个线性无关的特征向量时就可以来玩啦！

这时候我们就可以在对角阵当中找比较大的啦，他们就是代表了！

SVD

特征值分解不挺好的嘛，但是它被限制住了，如果我的矩阵形状变了呢？

但是问题也来了，如果M和N都很大呢？

 

照样按照特征值的大小来进行筛选，一般前10%的特征值（甚至更少）的和就占到了总体的99%了。

取前K个来看看吧！

 

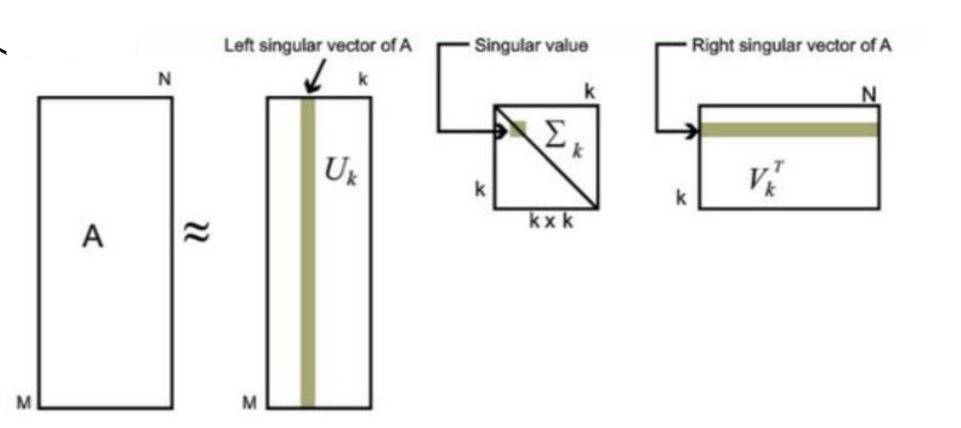
SVD推导

前提：对于一个二维矩阵M可以找到一组标准正交基v1和v2使得

Mv1和Mv2是正交的。

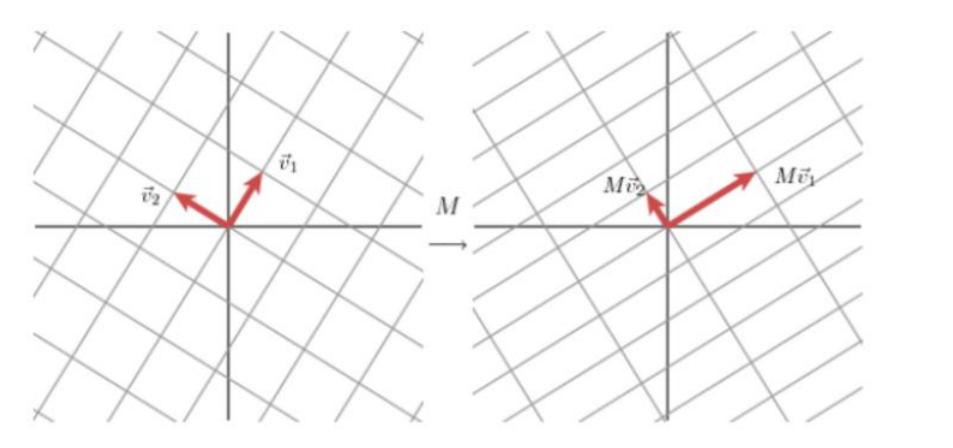
 SVD推导

使用另一组正交基u1和 u2来表示Mv1和 Mv2的方向；

其长度分别为：||MV1|| = σ1，||MV2|| = σ2，可得MV1 =  σ1u1，MV2 =  σ2u2 

对于向量X在这组基中的表示： x = (v1*x)v1 + (v2*x)v2 ，（点积表示投影的长度，可转换成行向量乘列向量 v*x = v^T x） 

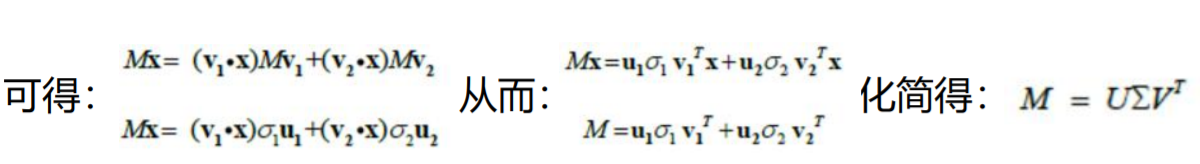
6. 随机变量

连续与离散随机变量（数值化实验的各种结果）

 

离散型随机变量

概率函数（概率质量函数）

• 专为离散型随机变量定义的：P(x) = Prob(X=x) ；
• 本身就是一个概率值，X是随机变量的取值，P就是概率了；
• 比如我们来投掷筛子；

离散型随机变量概率分布

　　找到离散型随机变量X的所有可能取值；

　　得到离散型随机变量取这些值的概率

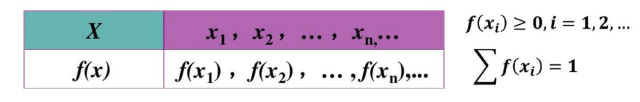
　　f(x_i) = P(X=x_i) 为离散型随机变量的概率函数；

  房间中介一天卖出房源数量

 

 

连续型随机变量 

如何理解概率函数和概率分布呢

概率密度:对于连续型随机变量X,我们不能给出其取每一个值的概率，也就是画不出那个分布表,这里我们选择使用密度来表示其概率分布!

假设我有一组零件,由于各种因素的影响,其长度是各不相同的。

概率密度函数

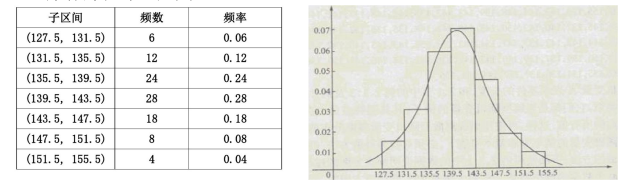
离散型的我们已经知道咋办啦,那按照这个思路我们先简单分个组

 

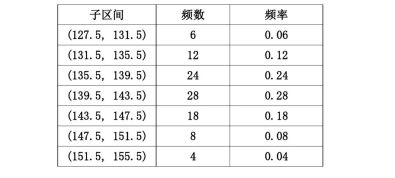
绘制频率分布直方图

这样看起来有点粗糙,当我们把样本数据增加,分组数也同时增加,这样的轮廓是不是会越来越细致呀!接近于一条曲线,这不就是我们想要的嘛!

 

密度:一个物体,我们如果问其中一个点的质量是多少?这该怎么求呢?由于这个点实在太小了,那么质量就为0了。但是其中的一大块是由很多个点组成的,这时我们就可以根据密度来求其质量了!

X为连续随机变量,X在任意区间(a,b]上的概率可以表示为:

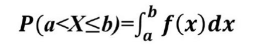
其中f(x) 就叫做X的概率密度函数, 也可以简单叫做密度.

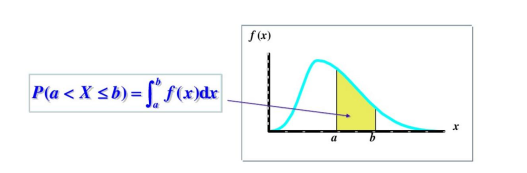
概率密度函数用数学公式表示就是一个积分,也可以把概率形象的说成面积!

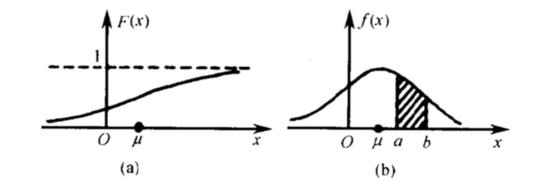
 图(a)是连续型随机变量的分布函数,  图(b)是其概率密度函数图像。

 

简单随机抽样

抽取的样本满足两点:

• (1)样本X1,X2...Xn是相互独立的随机变量。
• (2)样本X1,X2...Xn与总体X同分布。

联合分布函数:

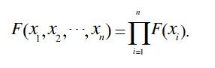
联合概率密度:

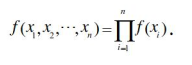
似然函数

似然函数

给定联合样本值x关于参数θ的函数：L(θ| x) = f(x| θ)， 其中x是随机变量X取得的值，θ是未知的参数。

f(x| θ)是密度函数，表示给定θ下的联合密度函数。

似然函数是关于θ的函数而密度函数是关于x的函数。

 

离散情况下

概率密度函数： f(x| θ) = P_θ(X=x) ，表示在参数θ的下随机变量X取到x的可能性；

     

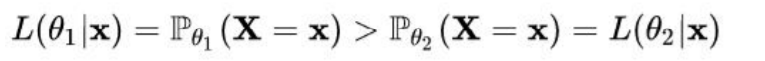
如果有上式成立，则在参数θ1下随机变量X取到x值的可能性大于θ2；

 

连续情况下

如果X是连续随机变量给定足够小的ε>0，那么其在(x-ε,x+ε)内的概率为：

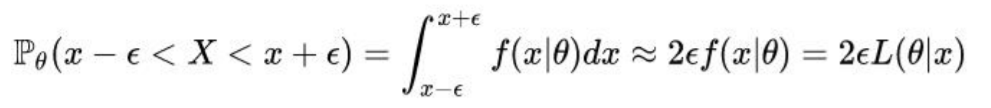
得到的结果与离散型一致！概率表达了在给定参数θ时X=x的可能性， 而似然表示的是在给定样本X=x时，参数的可能性！

 

极大似然估计

谁干掉的多？

在一次吃鸡比赛中，有两位选手，一个是职业选手，一个是菜鸟路人。 比赛结束后，公布结果有一位选手完成20杀，请问是哪个选手呢？

估计大家都选的是职业选手吧！ 因为我们会普遍认为概率最大的事件最有可能发生！

极大似然估计：在一次抽样中，得到观测值x1,x2...xn。 选取θ'(x1,x2...xn)作为θ的估计值，使得θ=θ'(x1,x2...xn)时样本出现的概率最大。

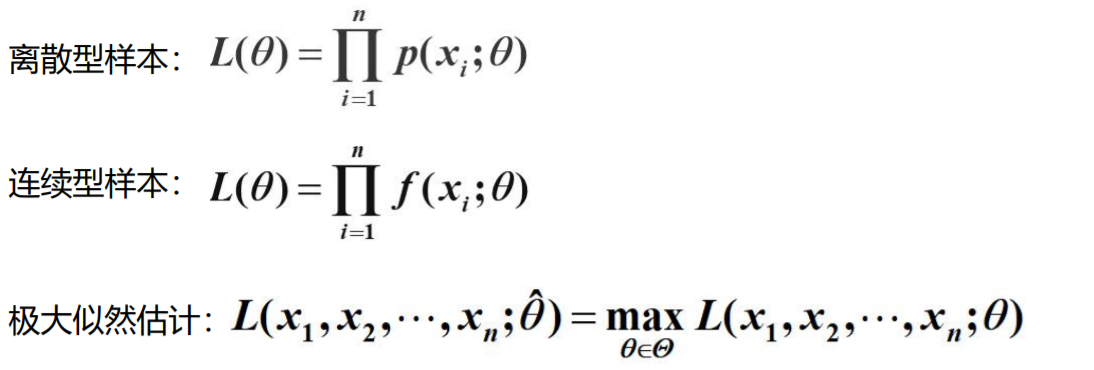
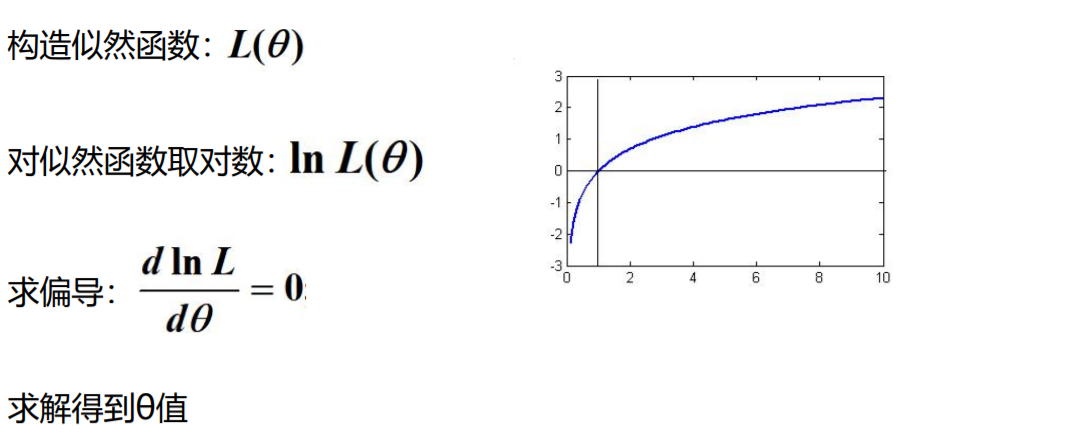
 极大似然估计求解

 

 

 

 

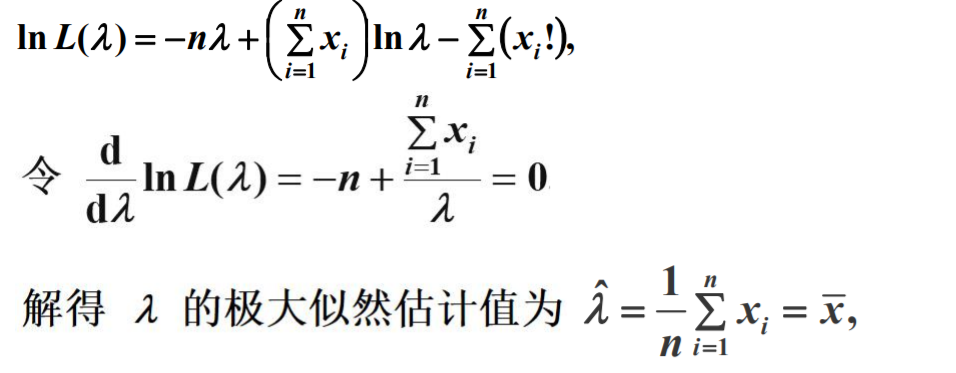
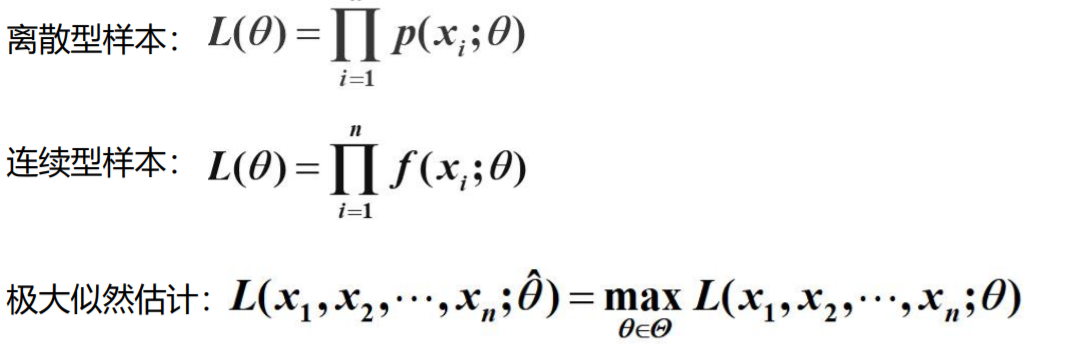
后验概率估计

回顾最大似然估计

 最大似然估计

 

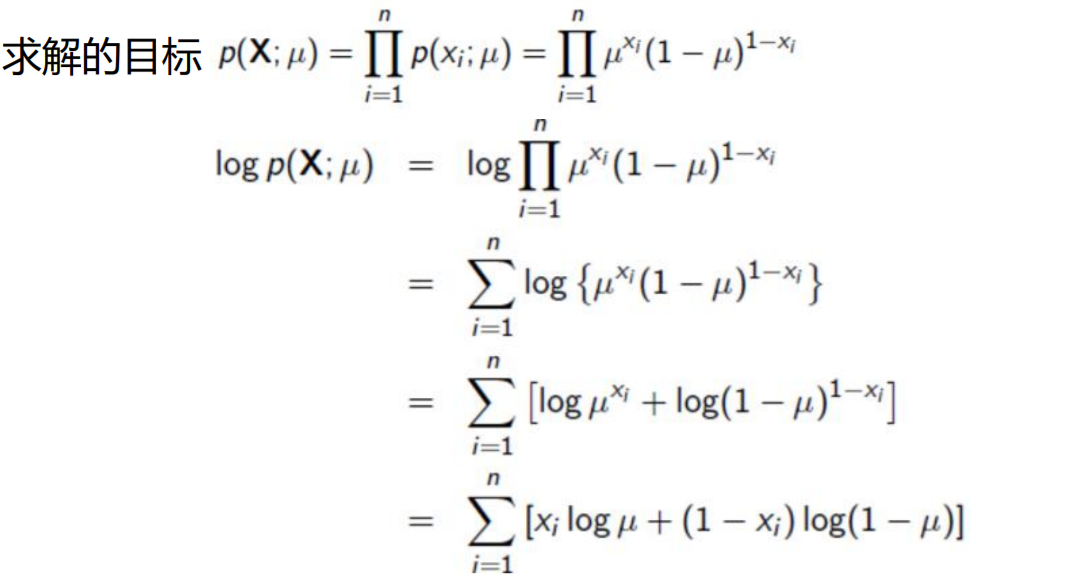
最大后验概率有啥区别吗

要求的东西变了吗？好像木有，都是做参数估计。

问题变得复杂一点了，现在多了一个先验知识。

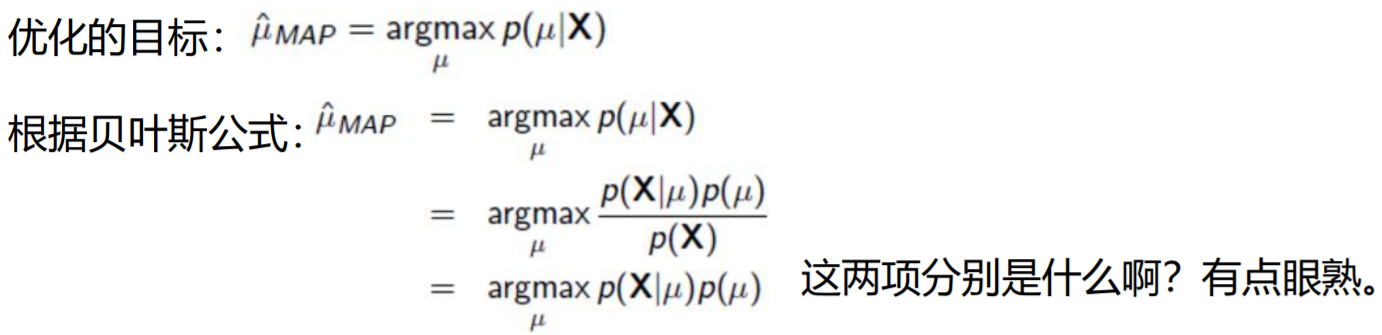
 最大后验估计

 

 

 

7. 概率论基础

概率论是研究随机现象数量规矩的数学分支；

随机事件是什么呢?

扔硬币,王者峡谷击杀数,一批产品合格数，这些有什么特点呢?

• 1.可以在相同条件下重复执行
• 2.事先就能知道可能出现的结果
• 3.试验开始前并不知道这一次的结果

随机试验E的所有结果构成的集合称为E的样本空间 S = { e } 

抛硬币：S = {正面,  反面} 

击杀数：S = {0, 1, 2,...} 

频率与概率

• A在这N次试验中发生频率： f_n(A) = n_A / n 
  • 其中，n_A是A发生的次数(频数)； n是总试验次数； 
• f_n(A) 的稳定值P定义为A的概率 P(A) = p  

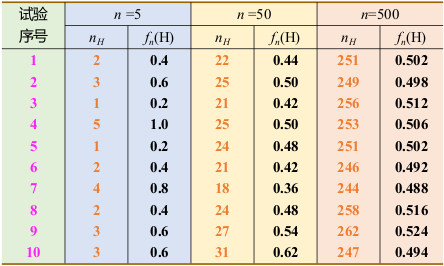
古典概型

定义：试验E中样本点是有限的，出现每一样本点的概率是相同； 

　　P(A) = A所包含的样本点数 / S中的样本点数 

一袋中有8个球, 编号为1-8, 其中1-3号为红球, 4-8号为黄球, 设摸到每一球的可能性相等, 从中随机摸一球, 记A={ 摸到红球 }, 求P(A)。

　　S = {1, 2, 3,...8} 

　　A = {1, 2, 3}   ==> P(A) = 3/8 

条件概率

3张奖券中只有1张能中奖,现分别由3名同学无放回地抽取, 问最后一名同学抽到中奖奖券的概率是否比其他同学小?

Y表示抽到了, N表示木有抽中, 所有的可能情况为: Ω = {YNN, NYN, NNY} ，B表示最后那个同学中了：B = {NNY} 

有古典概率可知：P(B) = n(B) / n(Ω) = 1 / 3 ，一般用Ω 表示所有基事件的集合； 

 

如果已经知道第一个同学没抽中，那最后一名抽中的可能性会变吗？

第一名没中则：A = {NYN, NNY} 

B事件依旧表示最后那同学中了：B = {NNY} 

那第一未中，第三中的事件发生的概率: P(B| A) = n(B) / n(A) = 1 / 2 

 

为什么结果不一样呢？什么变了？

未知第一个同学时，样本空间为：Ω = {YNN, NYN, NNY} 

知道第一同学未中时，样本空间为：A = {NYN, NNY} 

但是第三个同学中奖的情况依旧只有一种：{NNY} 

 

样本空间是什么样？

P(B) 以试验下为条件，样本空间是 Ω ；

P(B| A) 以A 发生为条件，样本空间缩小为A ; 

    P(B| A) 相当于把A 看作新的样本空间求A B 发生的概率；

 

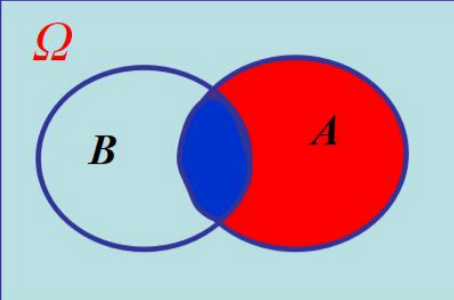
P(B|A)的求解思路：

　　P(B| A) 的求解思路：P(B| A) = n(AB) / n(A) 

因为已经知道事件A必然发生，所以只需在A发生的范围内考虑问题，即现在的样本空间为A。

因为在事件A发生的情况下事件B发生，等价于事件A和事件B同时发生，即AB发生。

   P(B| A) = n(AB)/n(Ω) / n(A)/n(Ω) =  P(AB) / P(A)

 

P(B|A)与P(AB)

相同点：事件A，B都发生了

不同点：

• 样本空间不同：在P(B|A)中，事件A成为样本空间；
• 在P(AB)中，样本空间仍为Ω 。

 

例题

甲乙两地都位于长江下游，根据一百多年的气象记录，知道甲乙两地一年

中雨天所占的比例分别为20％和18％，两地同时下雨的比例为12％，问：

设A={甲为雨天}， B={乙为雨天}则P(A)=20%，P(B)=18%，P(AB)=12%

（1）乙地为雨天时甲地也为雨天的概率是多少？

　　P(A| B) = P(AB) / P(B) = 12%/ 18% = 2 / 3

（2）甲地为雨天时乙地也为雨天的概率是多少？

　　P(B| A) = P(AB) / P(A) = 12% / 20% = 3 / 5 

 

例题

某厂生产的产品能直接出厂的概率为70%，余下的30%的产品要调试后再定，

已知调试后有80%的产品可以出厂，20%的产品要报废。求该厂产品的报废率。

设 A = {生产的产品要报废} 

     B = {生产的产品要调试} 

已经P(B) = 0.3，P(A| B) = 0.2，P(A|  ¯B) = 0 

P(A) = P(AB ∪ A  ¯B) = P(AB) + P(A ¯B)  

        = P(B) . P(A| B) + P(¯B) . P(A| ¯B)

        = 0.3 * 0.2 + 0.7 * 0 

        = 6% 

 

独立性

设A, B 为两随机事件，若P(B| A) = P(B) ，即P(AB) = P(A) * P(B) 

即P(A| B) = P(A) 时，称A, B相互独立。

 但是两两独立并不能得出相互独立。

例题

甲、乙两人同时向一目标射击，甲击中率为0.8，乙击中率为0.7，

求目标被击中的概率。

设 A = {甲击中}，B = {乙击中}，C = {目标被击中} 

则：C = A ∪ B， P(C) = P(A) + P(B) - P(AB) ，甲、乙同时射击，其结果互不影响，A、b相互独立；

       P(C) = 0.7 + 0.8 - 0.56 = 0.94 

 

独立试验

重复独立试验：在相同的条件下，将试验E重复进行，且每次试验是独立进行的，即每次试验各种结果出现的概率不受其他各次试验结果的影响。

n重伯努利试验：若一试验的结果只有两个A和Ā, 在相同的条件下, 将试验独立地重复进行n次, 则称这n次试验所组成的试验为n重复伯努利试验或伯努利概型。

 

将一枚均匀的骰子连续抛掷3次，考察六点出现的次数及相应的概率。

设六点出现的次数为X，设第i 次抛掷中出现6点的事件为A_k,K = 1, 2, 3 ，则 

 

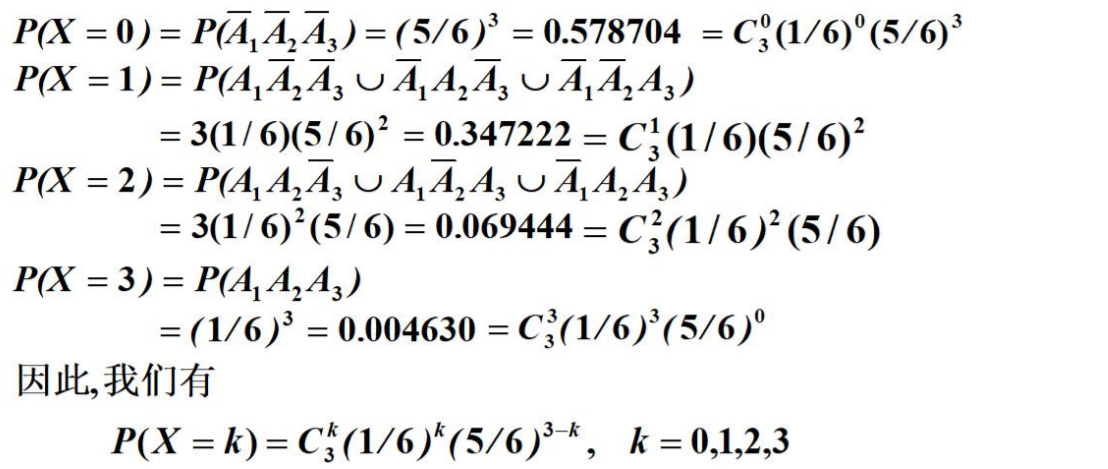
n重伯努利试验

如果每次试验中事件A发生的概率为 P(0 < p < 1)，

则在n次贝努里试验中事件A 恰好发生k次的概率为 

 

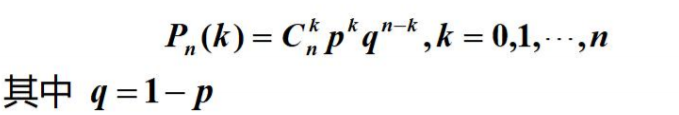
二维随机变量

以前我们只关心一个指标，现在要更操心了，例如根据学生的身高（X）和体重（Y）来观察学生的身体状况。

这就不仅仅是X和Y各自的情况，还需要了解其相互的关系。

 

二维随机变量

二维随机变量的联合函数：若（X,Y）是随机变量，对于任意的实数x,y

  F(x, y) = P{(X <= x ∩ (Y <= y))} 

F(x,y)表示随机点（X,Y）在以（x,y）为顶点且位于该点左下方无穷矩形内的概率。

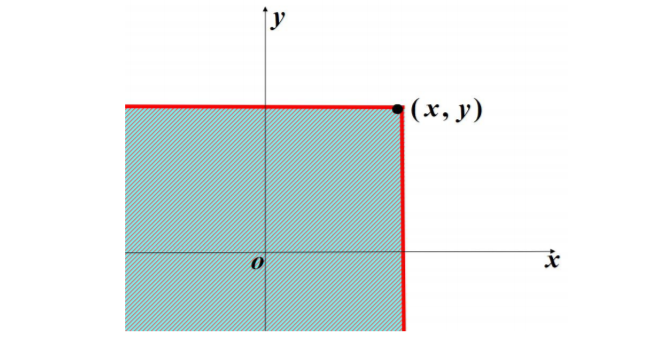
 二维随机变量

用联合分布函数F(x,y)表示矩形域概率

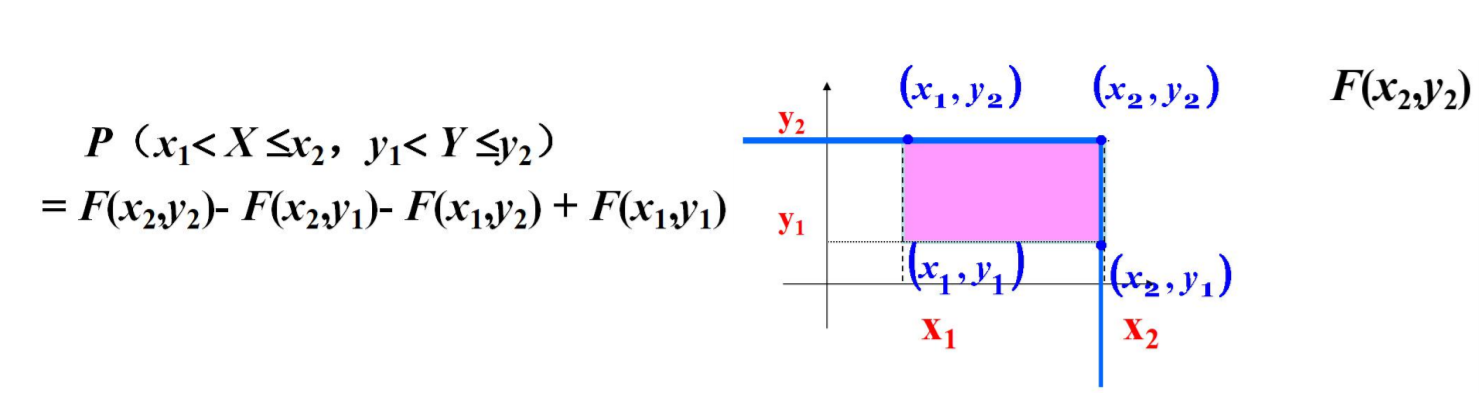
二维随机变量性质

 

 

设随机变量X在1、2、3、4四个整数中等可能地取 一个值，另一个随机变量

Y在1~X中等可能地取一整数值，试求(X,Y)的联合概率分布。

 二维连续型随机变量

 

 

边缘分布

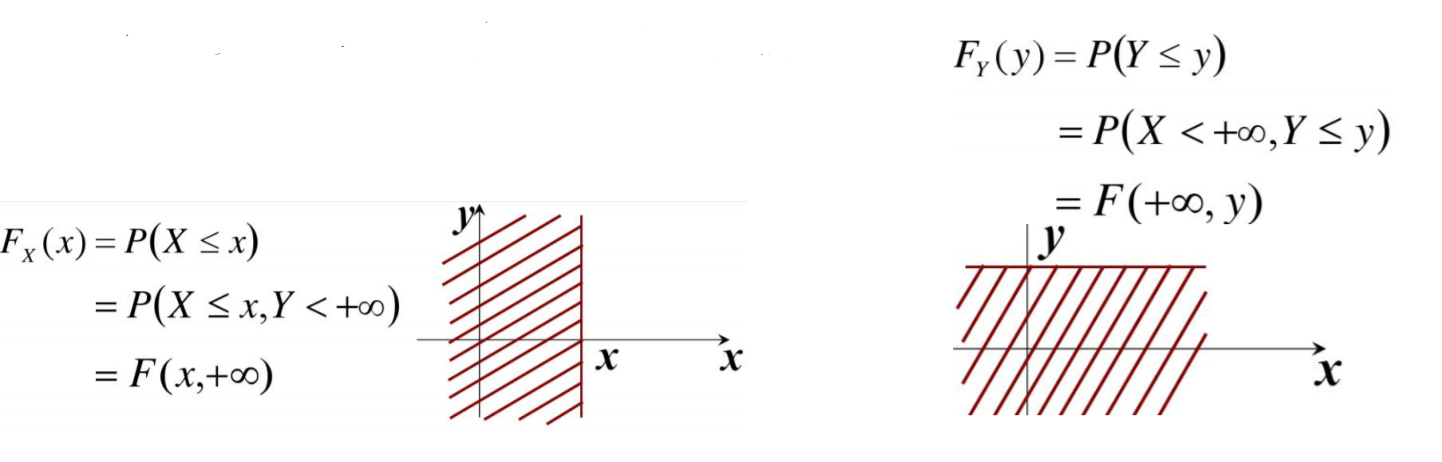
边缘分布函数：二维随机变量(X,Y)作为整体，有分布函数F(x, y)， 其中，X和Y都是随机变量，它们的分布函数记为：F_X(x), F_Y(y)  称为边缘分布函数。

 

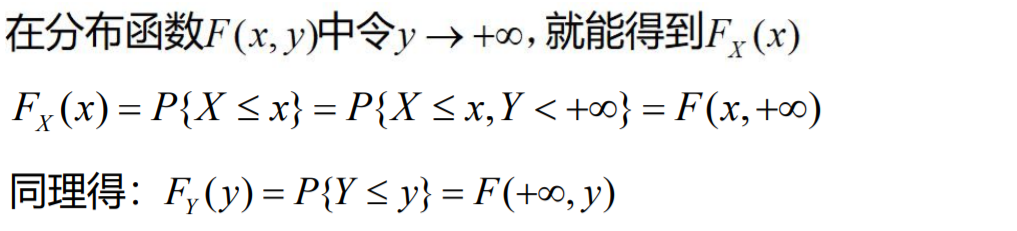
概边缘分布

由联合分布函数可以得到边缘分布函数：

 离散型的边缘分布

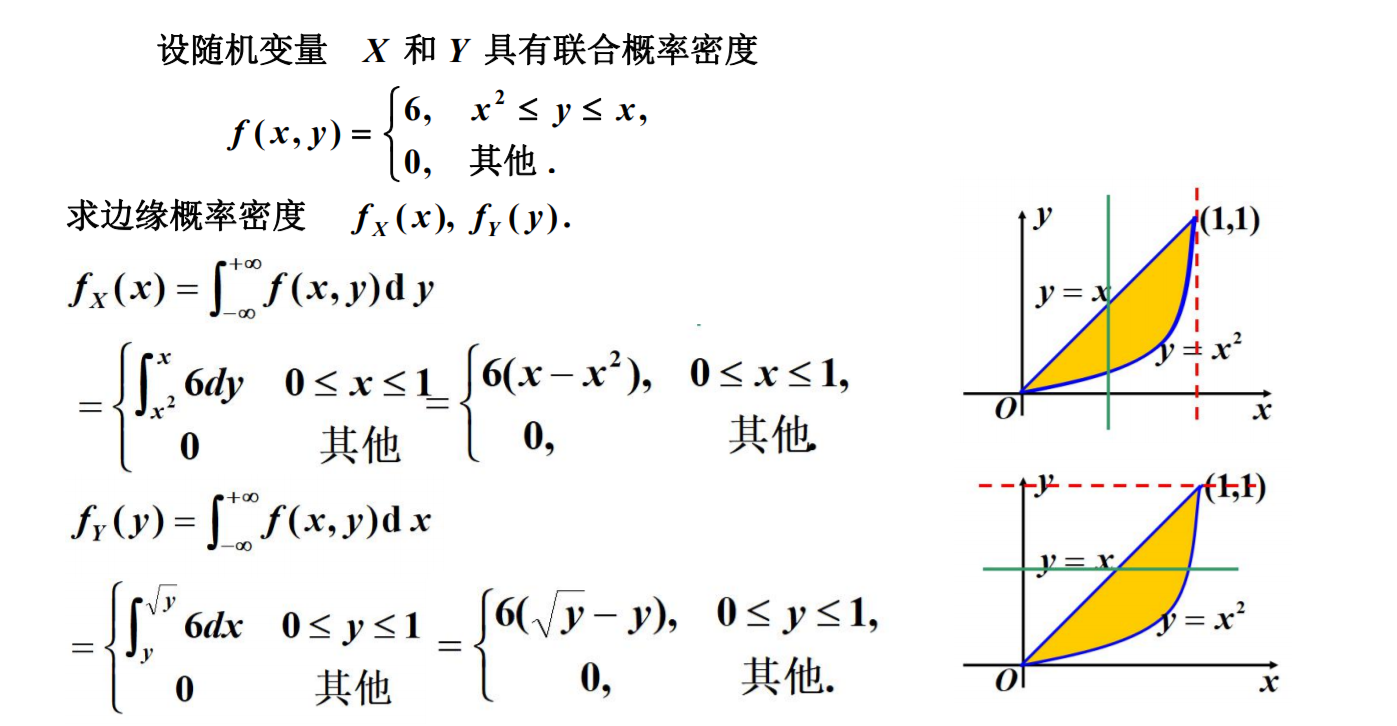
 连续型的边缘概率密度

 

 

 期望

 

 二维情况

 

 期望

 数学期望的性质

 

 方差

 大数定理：

在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。

小的样本试验不足以以偏概全因为有一些局限。

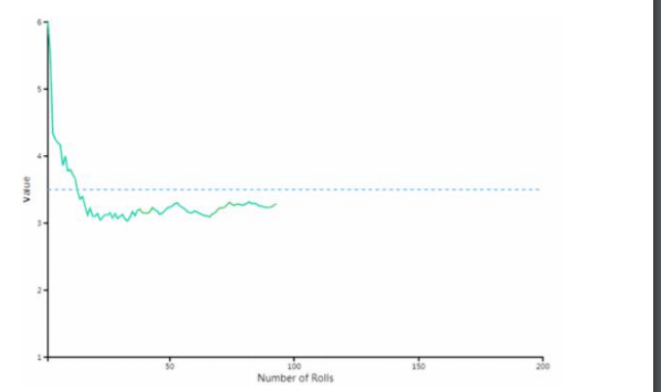
当我们投掷骰子的时，期望会等于多少呢？

马尔科夫不等式

 

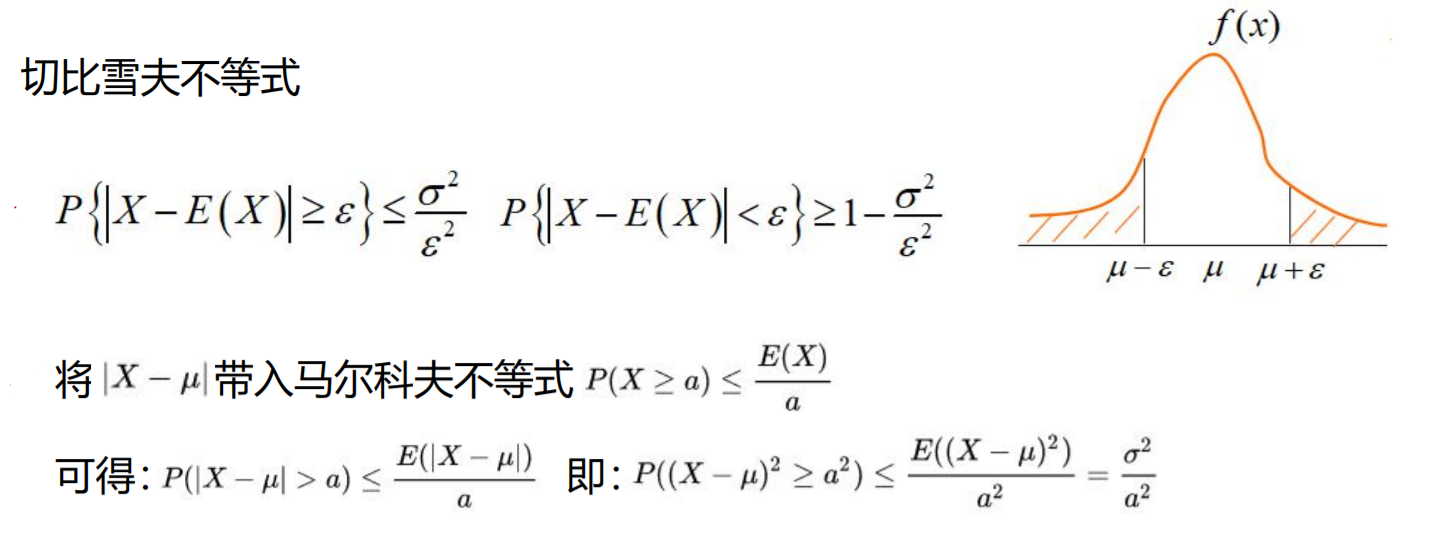
在n重贝努里试验中，若已知每次试验事件A出现的概率为0.75，试利用 契比雪夫不等式估计n，使A出现的频率在0.74至0.76之间的概率不小于0.90。

中心极限定理

样本的平均值约等于总体的平均值。不管总体是什么分布，任意一个总体 的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

描述的是一个实际的现象，有了这个定理就能解决很多问题了，比如我们 可以通过对样本进行观察，得出总体的情况。

https://onlinestatbook.com/stat_sim/sampling_dist/index.html