十二. 主成分分析-PCA

主成分分析-PCA

聚类分析（cluster analysis）是一组将研究对象分为相对同质的群组（clusters）的统计分析技术 ---->>

将观测对象的群体按照相似性和相异性进行不同群组的划分，划分后每个群组内部各对象相似度很高，而不同群组之间的对象彼此相异度很高。

Principal Component Analysis, PCA主成分分析

最广泛无监督算法 + 基础的降维算法；
通过线性变换将原始数据变换为一组各维度线性无关的表述，用于提取数据的主要特征分量 - 高维的降维；

一个样本的特征非常多且样例特别少，直接拟合容易过拟合，所以通过降维的方法，把多维度变成核心的几个维度；

1. 数据的降维

高维数据

除了图片、文本数据，我们在实际工作中也会面临更多高维的数据。比如在评分卡模型构建过程中，我们通常会试着衍生出很多的特征，最后就得到上千维、甚至上万维特征; 在广告点击率预测应用中，

拥有几个亿特征也是常见的事情; 在脑科学或者基因研究中，特征数甚至可能更多; 所以，如何更有效地处理这些高维的特征就变成了一个非常重要的问题。

高维转低维，转换为向量的形式，v是指词库的大小；

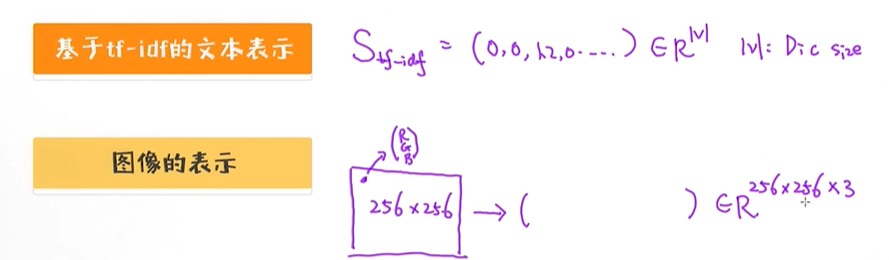
数据降维

对原有的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

除了有效利用高维的数据之外，我们也可以思考一个问题:“高维数据，那么多特征真的都有用吗?” 这就类似于一个人的社交质量并不取决于有多少朋友，而在于朋友质量，在建模过程中也适用这个道理。

特征越多并不代表学出来的模型越好，我们更需要关注特征对预测任务的相关性或者价值，有些特征甚至可能成为噪声，反而影响模型的效果。

在数据挖掘领域，有这样的一句话:“Better Representation always lies in a lower dimensional space”，究竟如何理解这句话呢?

比如有一个图片是100*100，我们用1万维的向量或3万维向量来表示，但这并不是一个图片最好的表示，最好的表示在更低维的空间；因为在原始空间的表示可能存在些噪声，特征是冗余的、或者没有价值的等因素造成原来的表示不是一个最优的，最优的表示通常在更低维的空间里面；

用向量表示一个人的特征

低维空间的表示的优点

可视化：R^{100 ——>} R²/ R³
更高效地利用资源 R¹⁰⁰⁰ ——> R²⁰ （比如硬件资源）
更强的泛化能力 R¹⁰⁰⁰ ——> R²⁰ （模型的适应能力更强，模型越复杂越容易过拟合）
去除噪声（比如数据可能不太准确等等）

如何去寻找更低维空间的表示？（高维转低维）

数据的降维（假设f是线性的，为一个2*3的矩阵）
特征的选择（x2次要特征）

2. PCA的核心思想

比如原数据从100个变量降为10个新变量，这10个新变量分别由这100个旧的变量组成，a1b1 + a2b2 +...+ a10b10，b1~b10按照由大到小排列，并做累计求和 -->贡献率；

一般选取贡献率达到85%以上的成分作为主要成分，比如筛选后，b1、b2、b3的累计贡献率超过85%，则筛选出a1, a2, a3作为该样本数据的主成分，总而实现降维；

求解步骤：

计算数据的协方差矩阵；
计算协方差矩阵的特征值与特征向量；
特征值从大到小排序；
筛选主成分，并将数据转换到特征向量构建的新空间中；

关于PCA的几个问题

PCA(Principal Component Analysis)作为一种重要的降维算法有着非常广泛的应用。PCA经常用来做数据的可视化、或者用来提高预测模型的效果。对于PCA降维算法来讲，有几个核心问题需要弄清楚:

PCA降维的核心思想是什么? 它是依赖于什么条件做降维?
什么叫主成分(principal component)?

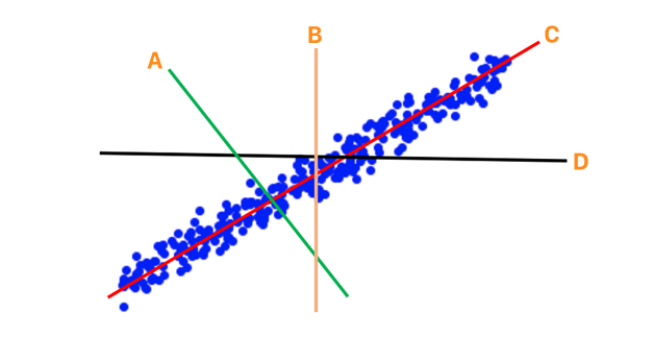
以上图片中的是二维数据的可视化展示。我们现在希望把上述数据映射到一维的空间, 或者可以理解为希望用一维来表示数据但同时保留原始数据的核心特点。

在图中给出了4条直线分别代表的是我们希望选择的坐标方向：

从图中可以看出, 沿着C的方向, 数据是越分散的, 也就说明在这个方向上我们可以看出数据之间的更多差异! 相反, 沿着直线A的方向, 我们可以看到很多数据的差异并不明显, 区分度很低。

所以,总体来讲, 当我们选择C为新的坐标轴时, 所有点在这个坐标轴上的值的差异是最大的, 也就是最大程度的保留了数据之间的特点(差异性) 方差, 这就是PCA的核心思想。

沿着这条线它的跨度最大，数据的方差是最大的，这个方向叫主成分；

如果通过PCA对数据进行转换

二维转一维如下图

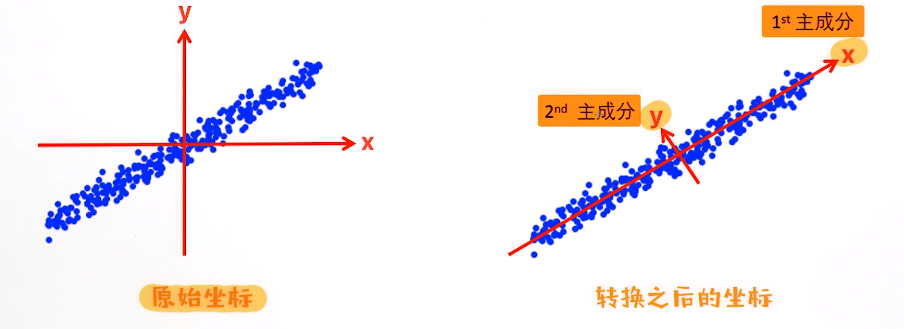
黑色点为样本，第一个主成分沿着绿色线方差最大，蓝色方向是第二个主成分；

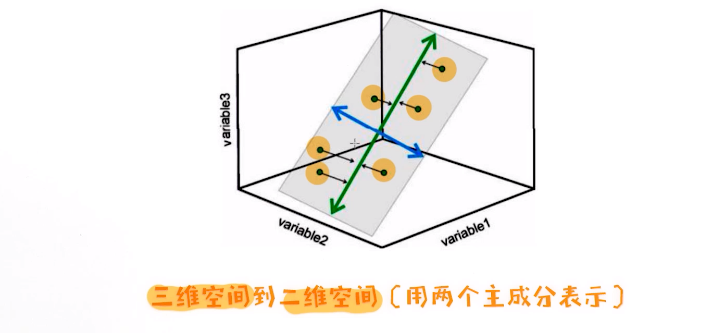
对于给定的二维数据，基于PCA映射到二维空间

用来把数据转换的矩阵tranformation matrix

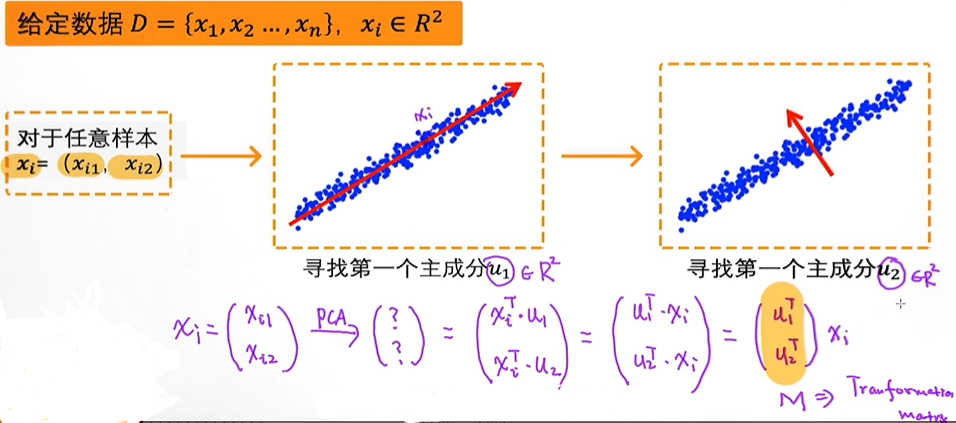
主成分的选取数量决定降维到多大的空间

通常来讲，如果原始数据的维度为

3. PCA的一些细节

PCA的推导过程

　　整个推导的核心是寻找PCA里的主成分；协方差矩阵 - Covariance Matrix

给定数据 D = {x₁, x₂, x₃..., x_n} ，x_i ∈ R^d ，寻找主成分u₁, u₂...

把原来数据挪到中心，数据的均值变成0；计算协方差矩阵 S；

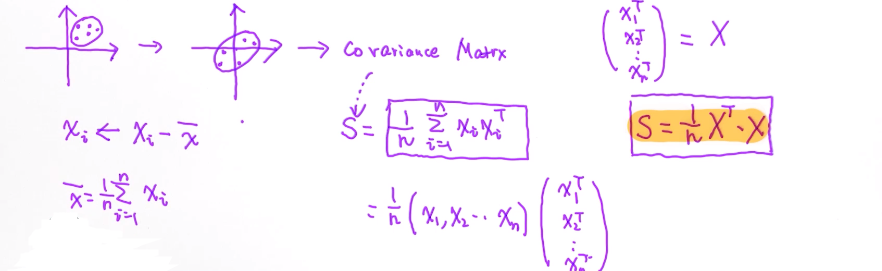
寻找第一个主成分u1，把每个值都映射到主成分上{u_1^Tx₁, u_1^Tx₂...}；

最大化方差σ_1² , 利用拉格朗日得到 L

有数据 -> 数据迁到中心的位置, 均值为0 -> 计算它的S协方差矩阵 -> 它的特征值和特征向量

二维空间的话就选取两个，五维空间的话选取5个特征向量；

需要选取多少个主成分

问题：取多少个主成分？

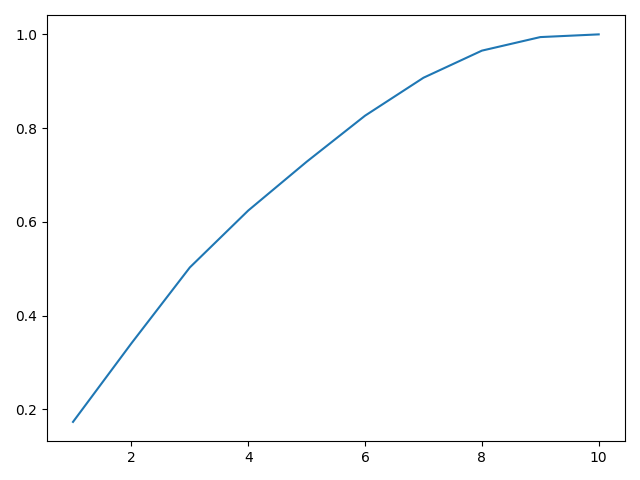
对于10维的数据，假如我们计算出了10个特征值：【30,29,28,21,18,17,14,10,5,1】，需要取多少个特征值呢？

特征值实际上代表了包含了多少信息量,从大到小排序后,选择前K个特征值使得信息量占比大于90%或者95%

首先, 我们要知道特征值代表的是信息量, 这个值越大就说明这个维度所包含的信息量就越大。我们先把特征值从大到小排序, 然后依次计算前K个特征值之和占所有特征值之和的百分比。

举个例子, 如果选取了前5个特征值, 然后他们之和占比已经在90%以上, 就说明前五个主成分基本上包含了所有的信息, 如果选取了前五个主成分, 数据就映射到了5维的空间。

方差存放信息的一种方式，目标值就是代表的方差；

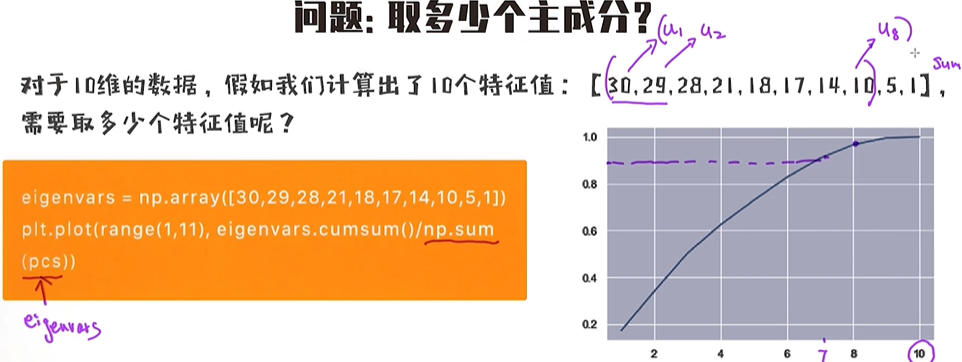
import numpy as np
import matplotlib.pyplot as plt

eigenvars = np.array([30, 29, 28, 21, 18, 17, 14, 10, 5, 1])
plt.plot(range(1, 11), eigenvars.cumsum()/np.sum(eigenvars))
plt.show()

PCA的实现

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
# 直接从sklearn导入iris数据
from sklearn.preprocessing import StandardScaler

data = load_iris()
# 读取特征、标签
X = data.data
y = data.target
# 做数据的归一化(必要的步骤!!!)
X_scaled = StandardScaler().fit_transform(X)
# 计算数据的covariance矩阵 cov = (1/n)* X'*X (X' 是 X的转置), n为样本总数
cov_matrix = np.matmul(X_scaled.T,X_scaled)/len(X_scaled)
# 根据cov_matrix计算出特征值与特征向量,调用linalg.eig函数
# https://numpy.org/doc/stable/reference/generated/numpy.linalg.eig.html
# eigenvalues存放所有计算出的特征值,从大到小的顺序
# eigenvectors存放所有对应的特征向量,这里 eigenvectors[:,0]表示对应的第一个特征向量
#  注:是列向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 根据计算好的特征向量,计算每个向量的重要性
import matplotlib.pyplot as plt
explained_variances = []
for i in range(len(eigenvalues)):
  explained_variances.append(eigenvalues[i] / np.sum(eigenvalues))
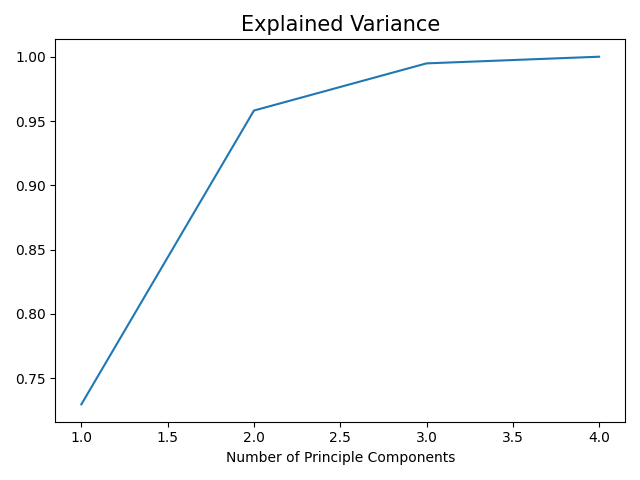
plt.plot(range(1,5),np.array(explained_variances).cumsum())
plt.title('Explained Variance',fontsize=15)
plt.xlabel('Number of Principle Components', fontsize=10)
plt.show()
# 把数据映射到二维的空间(使用前两个特征向量)
pca_project_1 = X_scaled.dot(eigenvectors.T[0]) #基于第一个特征向量的维度值
pca_project_2 = X_scaled.dot(eigenvectors.T[1]) # 基于第二个特征向量的维度值
# 构造新的二维数据
res = pd.DataFrame(pca_project_1, columns=['PCA_dim1'])
res['PCA_dim2'] = pca_project_2
res['Y'] = y
print (res.head())
import seaborn as sns
# 仅用第一个维度做可视化,从结果中会发现其实已经分开的比较好了
plt.figure(figsize=(20, 10))
sns.scatterplot(res['PCA_dim1'], [0] * len(res), hue=res['Y'], s=200)
# 用前两个维度做可视化,从结果中发现分开的比较好
plt.figure(figsize=(20, 10))
sns.scatterplot(res['PCA_dim1'], res['PCA_dim2'], hue=res['Y'], s=200)

PCA的缺点

PCA实际上做了线性转换（多个特征向量叠加一起得到一个新的矩阵，通过矩阵把每个样本做转换，矩阵转换就是线性转换），对于非线性数据效果不好；
必须要做特征的归一化（把数据挪到中心的位置）；

　　　　f₁：（0.1,0.2,0.4,0.7,0.3,0.6）；

　　　　f₂：（35,35.3,37,36.3,36,36.3,37,37）；

通过PCA，f2范围区间更大它的方差更大，但f1的差异性更明显；第二个特征比第一个特征方差更大，选择的方向倾向于 f2，所以一定要做归一化；

部分信息会丢失；（任何降维的算法都有这个缺点）
可解释性比较弱；（高维通过PCA映射到低维，每个维度代表什么含义是不知道的）

4. 其他降维的方法

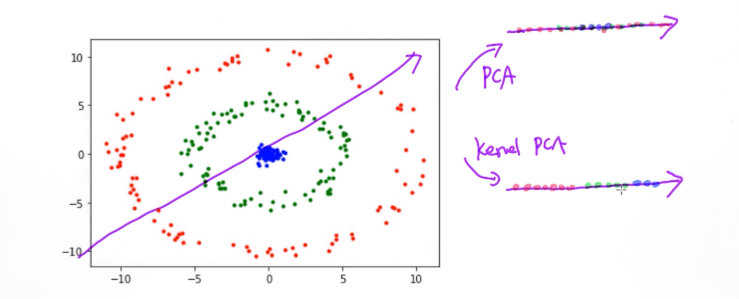
kernel PCA （可处理非线性的数据）
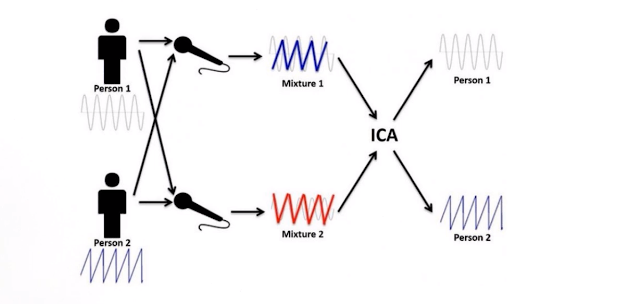
ICA（Independent component analysis ）
t-SNE （用于词向量可视化）
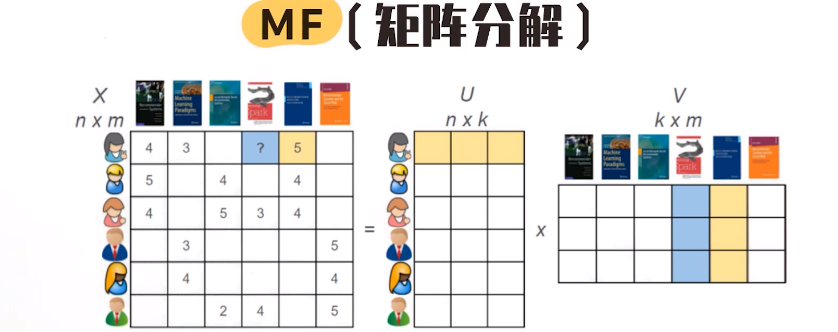
MF（Matrix Factorization）（矩阵分解，推荐系统）
Deep Learning （深度学习）

kernel PCA

使用核函数技巧的PCA；

ICA（Independent component analysis）

t-SNE

词向量

MF（Matrix Factorization）

Deep Learning

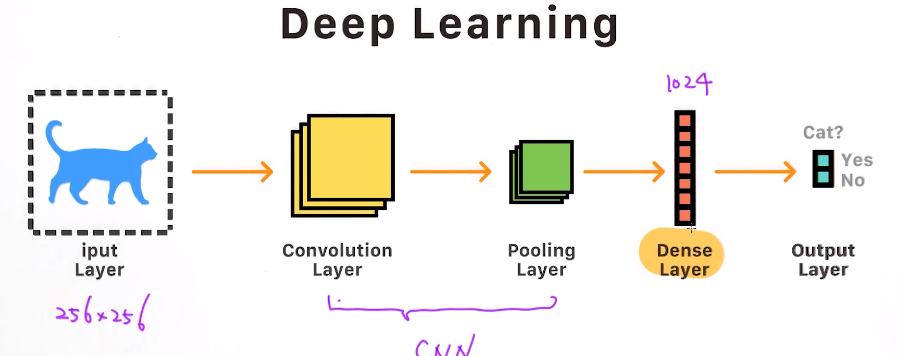
卷积神经网络CNN

5. 基于PCA的人脸识别

基于PCA的人脸识别

在这个案例中，我们将使用PCA做人脸识别，主要分为两步:

利用PCA把64*64大小的图片映射到低维空间
在低维空间利用随机森林做分类

通过这个案例会学到:

如何展示图片
如果在图片上应用PCA
如何可视化特征值的ratio
如何选择合适的主成分个数
如何可视化eigenface
如何把数据降维
如果在降维的数据上训练分类模型

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# 直接从sklearn导入人脸识别数据
from sklearn.datasets import fetch_olivetti_faces
data = fetch_olivetti_faces()
print(data.keys())
# dict_keys(['data', 'images', 'target', 'DESCR'])

inputs=data.data
target=data.target
images=data.images
print(inputs.shape)  # 400张人脸图片，每个图片像素为64*64
# (400, 4096)

# 显示其中几张图片
plt.figure(figsize=(20,20)) # 设置fig大小
for i in range(10,30):  # 输出其中20张图片
    plt.subplot(4,5,i-9)  # 每行五张图片，总共四行
    plt.imshow(data.images[i], cmap=plt.cm.gray)
plt.show()

# 导入相应的库
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(inputs, target, random_state=365)

# 利用PCA把原来4096（64*64）维度的数据映射到100维上
pca = PCA(n_components=200, whiten=True)
# 在训练数据上学习主成分，并把训练数据转换成100维的数据
X_train = pca.fit_transform(X_train)
# 在测试数据上做同样的转换
X_test = pca.transform(X_test)

# 可视化前100个主成分（占比）
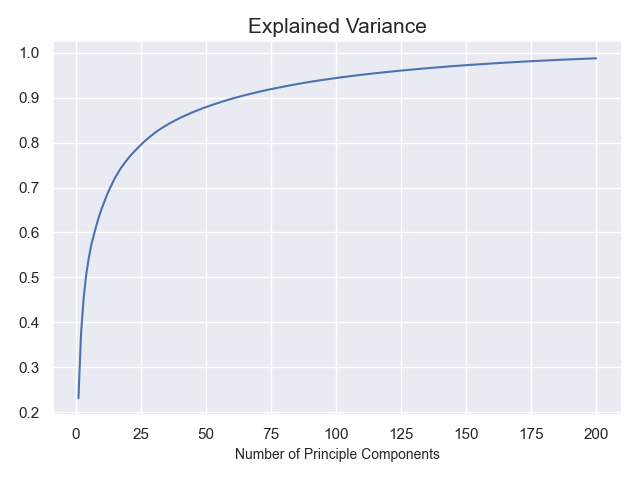
plt.plot(range(1,201), pca.explained_variance_ratio_.cumsum())
plt.title('Explained Variance',fontsize=15)
plt.xlabel('Number of Principle Components', fontsize=10)
plt.show()

# 从结果图中可以看出，当拥有100个主成分时已经将近接近了95%，所以我们可以选定利用前100个主成分

# 在这里，我们可视化主成分。对于人脸识别，我们把每一个主成分也称之为
# eigenface
plt.figure(figsize=(20,20)) # 设置fig大小
for i in range(0,20):  # 输出前20个主成分
    plt.subplot(4,5,i+1)  # 每行五张图片，总共四行
    # 可视化每一个主成分，可视化时需要reshape成64*64的矩阵形式，这样才能输出为图片
    plt.imshow(pca.components_[i].reshape(64,-1),cmap=plt.cm.gray)
plt.show()

# 利用随机森林图像的分类
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=500, random_state=0)
clf.fit(X_train, y_train)

# 计算一下分类准确率
accuracy_train= clf.score(X_train, y_train)
accuracy_test= clf.score(X_test, y_test)
print('Accuracy - train data: {}'.format(accuracy_train))
print('Accuracy - test data : {}'.format( accuracy_test))

# 计算一下f1-score
from sklearn.metrics import f1_score
test_pre=clf.predict(X_test)
train_pre=clf.predict(X_train)
f1_train=f1_score(y_train,train_pre,average='weighted')
f1_test=f1_score(y_test,test_pre,average='weighted')
print("f1 score - train data  : {}" .format(f1_train))
print("f1 score - test data  : {}" .format(f1_test))

　　Accuracy - train data: 1.0
　　Accuracy - test data : 0.94
　　f1 score - train data : 1.0
　　f1 score - test data : 0.9379365079365078

posted @ 2021-10-30 15:57 kris12 阅读(794) 评论(0) 收藏举报

刷新页面返回顶部

Arabic	Hebrew	Polish
Bulgarian	Hindi	Portuguese
Catalan	Hmong Daw	Romanian
Chinese Simplified	Hungarian	Russian
Chinese Traditional	Indonesian	Slovak
Czech	Italian	Slovenian
Danish	Japanese	Spanish
Dutch	Klingon	Swedish
English	Korean	Thai
Estonian	Latvian	Turkish
Finnish	Lithuanian	Ukrainian
French	Malay	Urdu
German	Maltese	Vietnamese
Greek	Norwegian	Welsh
Haitian Creole	Persian

kris12

Self-discipline gives me freedom.