论文阅读笔记：Andreas Loukas 图神经网络区分图能力的研究 —— How hard is to distinguish graphs with graph neural networks?

论文：Andreas Loukas. How hard is to distinguish graphs with graph neural networks? In NIPS 2020.

概要：图神经网络的一个特点是能够区分输入图的同构分类。本文研究了消息传递模型（MPNN）中图同构分类变体的硬度结果（Hardness Results）。MPNN涵盖了目前使用的大多数图神经网络，且当节点被赋予独特的特征时，MPNN是通用的。本文引入了通信容量以衡量网络节点在前向传播过程中可以交换多少信息，其取决于深度、消息大小、全局状态和架构宽度。研究表明，MPNN的容量需要随着节点数的增长而线性增长，这样网络才能区分树，而对于一般的连通图来说，容量则需要二次增长。导出的界限同时考虑了最坏情况和平均情况，并适用于具有/不具有独特特征和自适应结构的网络，它们也比简单论证给出的界限紧两个数量级。文中给出一项涉及12个图分类任务和420个网络的实证研究，其结果表明MPNN的实际性能和理论预测之间有很强的一致性。

1 定义

给定图$G = (\mathcal{V},\mathcal{E},a) \in \mathcal{X}$，$\mathcal{V},\mathcal{E},a$分别为节点集、边集和节点/边的特征。本文关注图同构分类，即需学得函数：$f: \mathcal{X} \rightarrow \mathcal{Y}$, $\mathcal{Y}$即图同构分类的集合。 

1.1 消息传播神经网络 (Message-passing Neural Networks，MPNN)

MPNN中节点表示 $x_{i}^{(\ell)}$ of every node $v_{i} \in \mathcal{V}$ 初始化为节点属性，即 $x_{i}^{(0)}=a_{i}$，且通过交换消息逐步更新:
$$
x_{i}^{(\ell)}=\operatorname{UPDATE}_{\ell}\left(x_{i}^{(\ell-1)},\left\{\operatorname{msg}_{i j}^{(\ell)}: e_{i j} \in \mathcal{E}\right\}\right) \quad \text { for } \quad \ell=1, \ldots, d
$$
每个消息为：
$$
\mathrm{msg}_{i j}^{(\ell)}=\operatorname{MESSAGE}_{\ell}\left(x_{j}^{(\ell-1)}, a_{j}, a_{i j}\right)
$$
其中包含了从节点 $v_{j}$ 传递到节点 $v_{i}$的一些信息.
一个网络中的每个神经元使用有限的字母表$\mathcal{S}$来编码自身的状态，字母表包含$s=|\mathcal{S}|$ 个符号。 由此，$x_{i}^{(\ell)}$ 和 $\mathrm{msg}_{i j}^{(\ell)}$ 分别选自 $\mathcal{S}^{w_{\ell}}$ 和 $\mathcal{S}^{m_{\ell}}$，其中 $w_{\ell}$ 和 $m_{\ell}$ 为 第$\ell$层的宽度和消息大小 。如果要求网络的输出独立于节点的数量，则通过readout函数从最后一层的表示中恢复输出：$g(G) = \operatorname{READOUT} (\{ x_{i}^{(d)} :v_i \in \mathcal{V} \})$，本文假设不使用pooling。

全局状态：上述的消息交换是沿着边发生的。对于某个特定节点来说，可定义一个全局状态扩充边集使之包含其他节点连向它的边。

自适应MPNN：MPNN的层数$d$可取决于输入图的大小和连通性，或其计算时间启发式地取决于节点表示的收敛性等。

1.2 通信容量 (Communication Capacity)

 将MPNN $g$ 和给定图 $G$ 看作一个通信网络$N(G,g)$：处理器为节点，其之间的连接由图$G$决定；$N(G,g)$在第$\ell = 1,...,d$轮次中同步通信，其中在第$\ell$轮中每个处理器向其每个邻居传送$m_{\ell}$个符号；每个处理器有轮次独立但有限的存储，在第$\ell$轮中每个处理器可存储$w_{\ell}$个符号，额外存储（全局状态）可存储$\gamma_{\ell}$个符号。

MPNN的通信容量（原文是communication complexity，疑似编辑错误）是$N(G,g)$中不相交的节点集之间可发送的最大信息量：

定义（通信容量）：给定MPNN $g$ 和图 $G=(\mathcal{V},\mathcal{E})$ ，对任意两个不相交的节点集$\mathcal{V}_a, \mathcal{V}_b \in \mathcal{V}$，$g$的通信容量$c_g$是$N(G,g)$中能从$\mathcal{V}_a$到$\mathcal{V}_b$和从$\mathcal{V}_a$到$\mathcal{V}_b$传送的最大符号数。

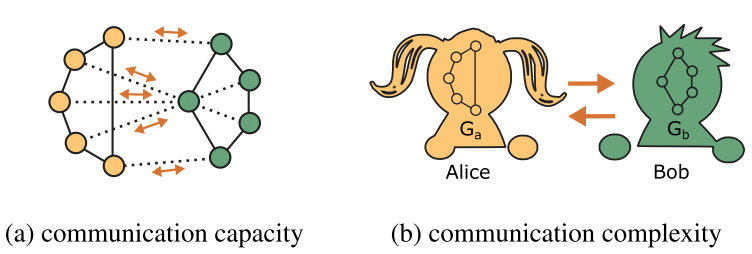
如图所示，假设$G$的两个不相交的子图$G_a=(\mathcal{V}_a,\mathcal{E}_a)$和$G_b=(\mathcal{V}_b,\mathcal{E}_b)$分别受Alice和Bob控制，则Alice给Bob发送信息须经过连接$\mathcal{V}_a$和$\mathcal{V}_b$的路径，反之亦然。由此观察可有推论——由MPNN前向传播传送的符号数受限于两个子图之间的割：

引理1.1：设$g$为$d$层的MPNN，其每层宽为$w_{\ell}$，消息大小为$m_{\ell}$，且维护一个大小为$\gamma_{\ell}$的全局状态。对任意$\mathcal{V}$的不相交的划分$\mathcal{V}_a$和$\mathcal{V}_b$，$g$的通信容量有上界为：

$$
c_{g} \leq \operatorname{cut}\left(\mathcal{V}_{a}, \mathcal{V}_{b}\right) \sum_{\ell=1}^{d} \min \left\{m_{\ell}, w_{\ell}\right\}+\sum_{\ell=1}^{d} \gamma_{\ell}
$$

其中$\operatorname{cut}\left(\mathcal{V}_{a}, \mathcal{V}_{b}\right)$为将$G$分为$\mathcal{V}_a$和$\mathcal{V}_b$的最小割的大小。

1.3 通信复杂度 (Communication Complexity)

现在假设Alice和Bob联合计算$f: \mathcal{X}_a \times \mathcal{X}_b \rightarrow \mathcal{Y}$，Alice / Bob输入为$x_a \in \mathcal{X}_a$ / $x_b \in \mathcal{X}_b$（对应$G_a$/$G_b$。Alice 和 Bob 计算$f(x_a,x_b)$需要基于协议$\pi$交换信息。对每个输入$(x_a,x_b)$，$\pi$决定一个交换信息符号的通信序列$\pi(x_a,x_b) = (({ID}_1,s_1,),({ID}_2,s_2),...)$，其中每个符号$s_i \in \mathcal{S}$与发送者（Alice或 Bob ）的id绑定。用$\| \pi(x_a,x_b)\|_m$表示成功计算$f(x_a,x_b)$需要使用$\pi$交换符号的数量，其中$m \in \{ one, both \}$表示在结束交换时是一方还是双方计算出$f(x_a,x_b)$。

$f$的最坏情况复杂度定义为：

$$
c_{f}^{m}:=\min _{\pi} \max _{\left(x_{a}, x_{b}\right) \in \mathcal{X}_{a} \times \mathcal{X}_{b}}\left\|\pi\left(x_{a}, x_{b}\right)\right\|_{m}
$$

即最坏输入情况下$\pi$的最小长度。

设$(X_a,X_b) \in \mathcal{X}_a \times \mathcal{X}_b $ 为取自分布 $\mathbb{D}$ 的随机变量，则$\pi$的期望长度为：

$$
\mathrm{E}_{\mathbb{D}}\left[c_{f}^{m}(\pi)\right]:=\sum_{\left(x_{a}, x_{b}\right) \in \mathcal{X}_{a} \times \mathcal{X}_{b}}\left\|\pi\left(x_{a}, x_{b}\right)\right\|_{m} \cdot \mathrm{P}\left(X_{a}=x_{a}, X_{b}=x_{b}\right)
$$

定义$f$的期望通信复杂度为：

$$c_{f}^{m} (\mathbb{D}):= \min _{\pi} \mathrm{E}_{\mathbb{D}}\left[c_{f}^{m}(\pi)\right]$$

2 确定同构分类的硬度结果

图同构分类即要学得一个从有标签的图到其同构分类的映射：$f_{isom}: \mathcal{X} \rightarrow \mathcal{Y}$。

下面将分析一个亚二次性/亚线性容量的MPNN不能计算计算连通图/树的同构分类。

定理2.1 设$g$是一个使用基于多数票或一致性Readout的MPNN，$c_g$为其通信容量：

　　1）对每个$n$个节点的图（树）计算$f_{isom}$，其必须满足$c_g = \Omega (n^2)$（ $c_g = \Omega (n)$）。

　　2）如果对每个都取自分布$\mathbb{B}_{n/2,p}$的图(取自$\mathbb{T}_{n/2}$的树)计算$f_{isom}$，其期望必须满足$c_g(\mathbb{D}) = \Omega (n^2)$ $c_g(\mathbb{D}) = \Omega (n)$）。

未完待续。。