P5005 中国象棋 - 摆上马

P5005 中国象棋 - 摆上马

题目背景

相信自己的做法 大喊一声 I won't MLE！您就会过这道题

Imakf 玩腻了国际象棋，决定玩一玩中国象棋。

他发现中国象棋的马和国际象棋的马有所不同，他意识到这又可以出一道简单的问题，于是他又准备摆一摆马了

题目描述

Imakf 有一个 \(X\) 行 \(Y\) 列的棋盘，还有很多完全相同的马（你可以认为有无数个）。现在在棋盘上摆上马（或者不摆），求任何马无法攻击另一匹马的方案总数。

中国象棋的马和国际象棋的马不同。

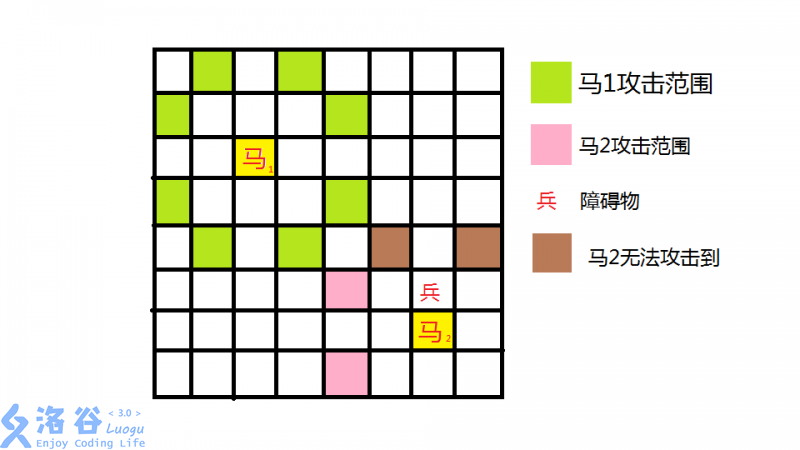
注意：实际问题中是没有兵的。

当然由于方案可能过多，请输出对 \((10^9+7)\) 取模的值

输入格式

第一行两个正整数 \(X,Y\)。

输出格式

方案对 \((10^9+7)\) 取模的值。

输入输出样例 #1

输入 #1

1 1

输出 #1

2

输入输出样例 #2

输入 #2

3 3

输出 #2

145

说明/提示

对于 100% 的数据，有 \(1\le X\leq100\)，\(1\le Y\leq6\)。

对于 20% 的数据，有 \(X,Y\leq6\)。

对于另外 20% 的数据，有 \(X\leq20\)。

对于样例 1，可以选择不摆或者摆。

对于样例 2，我有一个绝妙的解释可惜我写不下。

思路

本题思路极其简单，状压棋盘问题秒了，但是回头一看，这道题空间 1MB !!!

然后我直接写了记忆化之后发现爆了。

对此就肯定要针对空间展开优化，观察这道题的空间消耗，空间瓶颈主要在那个 \(mp[P][S][S]\) ，这里就爆炸了。

因此肯定要思考有没有空间浪费。观察可以发现在后两维之中，有很多不合法的方案也被计入进去了，但实际上它们的值都为 \(0\) ，这里就造成了空间浪费。

然后暴力打一个表之后就可以发现，如果只存合法方案，那么对应下来就是 \(mp[P][M]\) ,\(M=810\) 空间消耗是之前的 \(\frac 1 8\) 然后只需要另外开一个 \(vis[S][S]\) 数组，存储合法的两维状态对应的哈希值就可以了

然后这道题最多 800KB 过的，还是有点卡