P3574 [POI 2014] FAR-FarmCraft
P3574 [POI 2014] FAR-FarmCraft
题目描述
在一个叫做比特村的小村庄中,有 \(n-1\) 条路连接着这个村庄中的全部 \(n\) 个房子。
每两个房子之间都有一条唯一的通路。这些房子的编号为 \(1\) 至 \(n\)。
\(1\) 号房子属于村庄的管理员比特安萨尔。
为了提升村庄的科技使用水平,\(n\) 台电脑被快递到了比特安萨尔的房子。每个房子都应该有一台电脑,且分发电脑的任务就落在了比特安萨尔的肩上。
比特村的居民一致同意去玩农场物语这个游戏的最新快照版,而且好消息是他们很快就要得到他们最新的高配置电脑了。
比特安萨尔将所有电脑都装在了他的卡车上,而且他准备好完成这个艰巨的任务了。
他的汽油恰好够走每条路两遍。
在每个房子边,比特安萨尔把电脑贴心的配送给居民,且立即前往下一个房子。(配送过程不花费任何时间)
只要每间房子的居民拿到了他们的新电脑,它们就会立即开始安装农场物语。安装农场物语所用的时间根据居民的科技素养而定。幸运的是,每间房子中居民的科技素养都是已知的。
在比特安萨尔配送完所有电脑后,他会回到他自己的 \(1\) 号房子去安装他自己的农场物语。
用卡车开过每条路的时间恰好是 \(1\) 分钟,而居民开电脑箱的时间可以忽略不计。(因为他们太想玩农场物语了)
请你帮助比特安萨尔算出从开始配送到所有居民都玩上了农场物语的最少时间。
输入格式
第一行包含一个整数 \(n(2 \leq n \leq 5\times 10^5)\),代表比特村中有多少房子。
第二行包含 \(n\) 个整数 \(c_1, c_2, ⋯, c_n(1 \leq c_i \leq 10^9)\),每个数都被单个空格隔开。\(c_i\) 是第 \(i\) 号房间中居民安装农场物语所用的时间。
接下来的 \(n-1\) 行代表了每一条路的两个顶点。两个顶点 \(a\) 和 \(b\) 满足 \(1 \leq a < b \leq n\),两个数之间有一个空格。
输出格式
一行,包含一个整数,代表题目中所说的最小时间。
感谢@deadpool123 提供的翻译
输入输出样例 #1
输入 #1
6
1 8 9 6 3 2
1 3
2 3
3 4
4 5
4 6
输出 #1
11
题意概括
在树形村庄中,管理员从根节点出发,遍历所有节点分发电脑(每条边恰好经过两次),使得所有节点完成安装游戏的时间最大值最小化,最后返回根节点。
思路
这道题第一眼绝对不会有思路的,但像这种没有思路的题有很大可能是结论题或者性质题,甚至是神秘贪心,那么可以手玩一下样例。
手玩之后,其实可以发现,如果设 \(f_u\) 表示从 \(u\) 出发到其子树中,安装游戏的最大值,那么考虑在一个点 \(u\) 在面临决策:是先走 \(v_1\),还是先走 \(v_2\) 时,要让两个的代价最大值最小,那么第一个下去的代价是 \(f_{v_i}\) ,第二个下去的代价则是 \(2 \cdot (siz_{v_i}-1)+f_{v_2}\) ,那么这里就可以发现对于顺序安排的排序关键字就出来了,拍完序后基于此也就可以算出 \(f_u\) 然后就很简单了
P1772 [ZJOI2006] 物流运输
题目描述
物流公司要把一批货物从码头 A 运到码头 B。由于货物量比较大,需要 \(n\) 天才能运完。货物运输过程中一般要转停好几个码头。
物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在,有的时候某个码头会无法装卸货物。这时候就必须修改运输路线,让货物能够按时到达目的地。
但是修改路线是—件十分麻烦的事情,会带来额外的成本。因此物流公司希望能够订一个 \(n\) 天的运输计划,使得总成本尽可能地小。
输入格式
第一行是四个整数 \(n,m,k,e\)。\(n\) 表示货物运输所需天数,\(m\) 表示码头总数,\(k\) 表示每次修改运输路线所需成本,\(e\) 表示航线条数。
接下来 \(e\) 行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度。其中码头 A 编号为 \(1\),码头 B 编号为 \(m\)。单位长度的运输费用为 \(1\)。航线是双向的。
再接下来一行是一个整数 \(d\),后面的 \(d\) 行每行是三个整数 \(p,a,b\)。表示编号为 \(p\) 的码头在 \([a,b]\) 天之内无法装卸货物。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头 A 到码头 B 的运输路线。
输出格式
包括了一个整数表示最小的总成本。
总成本为 \(n\) 天运输路线长度之和 \(+ k \times\) 改变运输路线的次数。
输入输出样例 #1
输入 #1
5 5 10 8
1 2 1
1 3 3
1 4 2
2 3 2
2 4 4
3 4 1
3 5 2
4 5 2
4
2 2 3
3 1 1
3 3 3
4 4 5
输出 #1
32
说明/提示
【数据范围】
对于 \(100\%\) 的数据,\(1 \le n \le 100\),\(1\le m \le 20\), \(1 \le k \le 500\), \(1 \le e \le 200\)。
【样例输入说明】
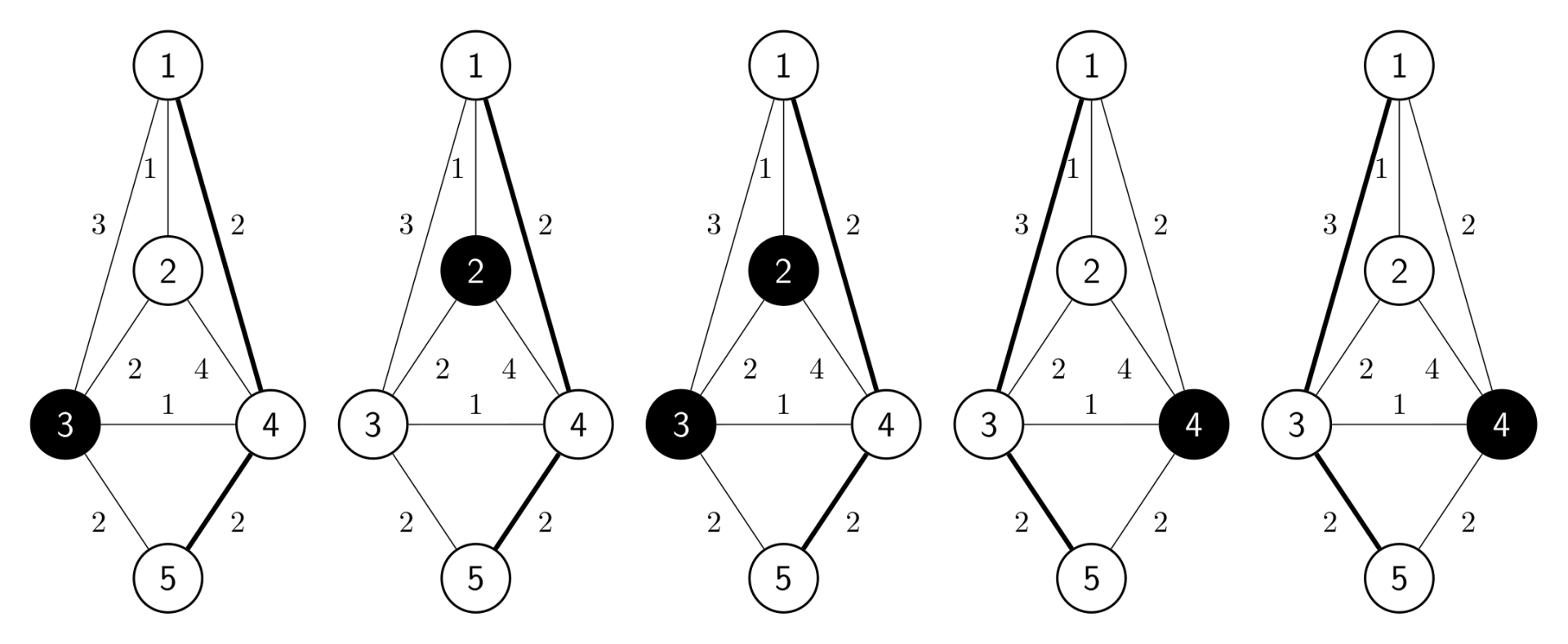
上图依次表示第 \(1\) 至第 \(5\) 天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走 \(1 \to 4 \to 5\),后两天走 \(1 \to 3 \to 5\),这样总成本为 \((2+2)\times 3+(3+2)\times 2+10=32\)。
_NOI导刊2010提高(01)
思路
这道题中,第 \(i\) 天的决策(或者说是答案)要受到前一天的影响,再加上这个神秘数据范围,那么肯定考虑dp
设 \(f_i\) 表示前 \(i\) 天的最小花费,那么状态转移显而易见:
计算 \(cost(l,r)\) 的时候可以预处理,也可以现做,跑一遍dijkstra就可以了,其中边的限制可以直接暴力维护,也可以用线段树区间修改区间查询的方式维护



 浙公网安备 33010602011771号
浙公网安备 33010602011771号