Trapped in the Witch's Labyrinth(搜索)

In the fourth labor of Rostam, the legendary hero from the Shahnameh, an old witch has created a magical maze to trap him. The maze is a rectangular grid consisting of \(n\) rows and \(m\) columns. Each cell in the maze points in a specific direction: up, down, left, or right. The witch has enchanted Rostam so that whenever he is in a cell, he will move to the next cell in the direction indicated by that cell.

If Rostam eventually exits the maze, he will be freed from the witch's enchantment and will defeat her. However, if he remains trapped within the maze forever, he will never escape.

The witch has not yet determined the directions for all the cells. She wants to assign directions to the unspecified cells in such a way that the number of starting cells from which Rostam will be trapped forever is maximized. Your task is to find the maximum number of starting cells which make Rostam trapped.

Input

The first line of the input contains an integer \(t\) (\(1 \leq t \leq 10^4\)), the number of test cases.

For each test case:

• The first line contains two integers \(n\) and \(m\) (\(1 \leq n, m \leq 1000\)), representing the number of rows and columns in the maze.
• Each of the next \(n\) lines contains a string of \(m\) characters representing the directions in the maze. Each character is one of the following:
  • U (up)
  • D (down)
  • L (left)
  • R (right)
  • ? (unspecified direction)

It's guaranteed that the sum of \(n \cdot m\) over all test cases is at most \(10^6\).

Output

For each test case, print a single integer, the maximum number of starting cells from which Rostam will be trapped forever after assigning directions to the unspecified cells optimally.

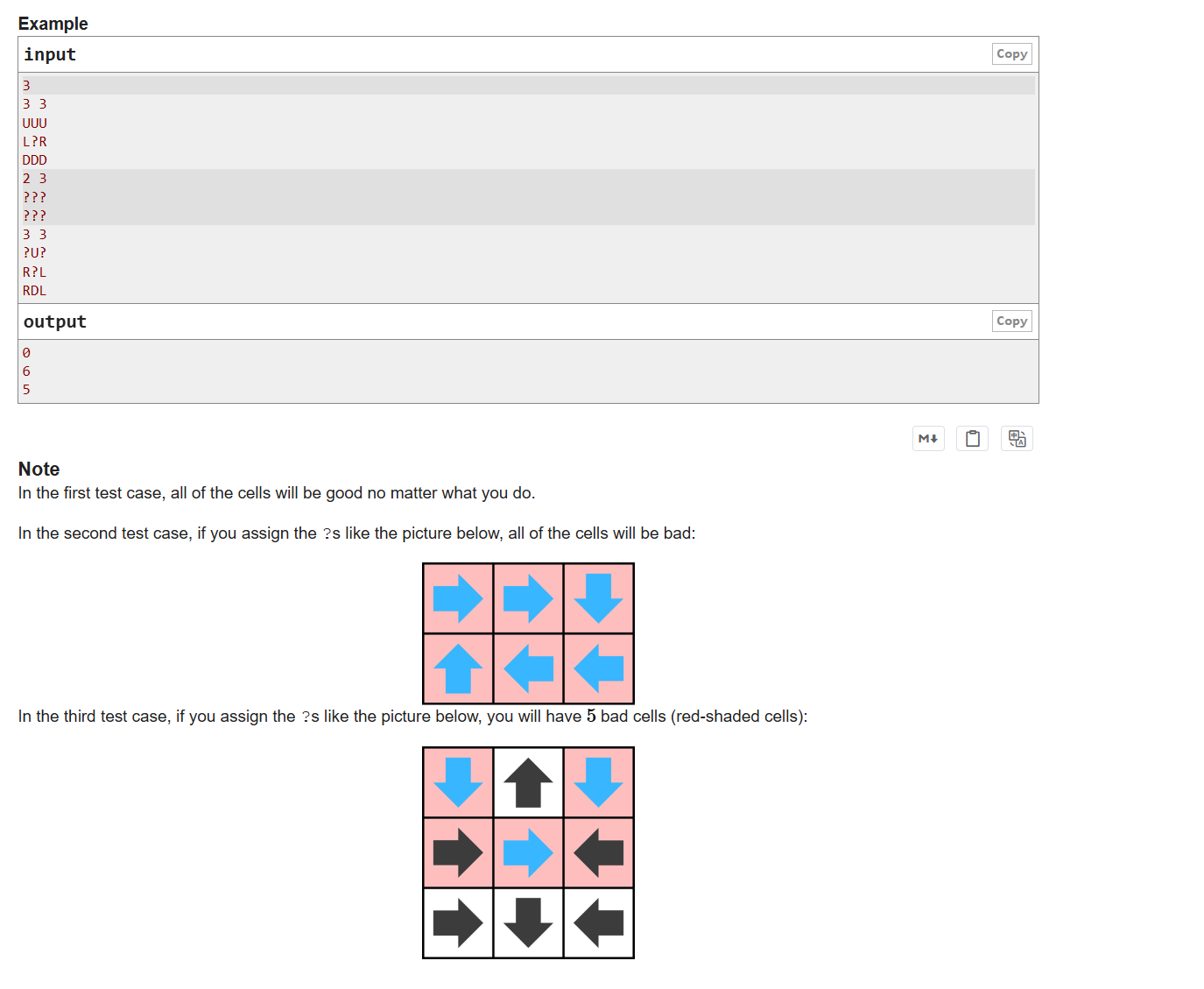
题意：给一 N 行 M 列的迷宫，其中有许多点给定了方向，问将剩下的点确定方向后能形成最大多大的循环路径？

官方题解：

• If a cell has a fixed direction (i.e., it points to another cell), and following that direction leads outside the maze, it must eventually exit the maze. Such cells cannot be part of any loop.
• We can analyze the remaining cells once we identify cells that lead out of the maze. Any undirected cell or \(?\) cell might either lead to the exit or form part of a loop.
• If all neighboring cells of a \(?\) cell can eventually lead out of the maze, then this \(?\) cell will also lead out of the maze. The state of such \(?\) cells can be determined based on their surroundings.
• For any remaining cells (directed cells that do not lead out of the maze, or other \(?\) cells that cannot be determined to lead to an exit), we can assign directions such that starting from those cells will eventually lead to a loop. These cells will form the loops.
• To find how many cells will eventually lead to a loop, we can use a Depth-First Search (DFS) on the reversed graph, where all directions are reversed. By performing DFS starting from the "out-of-maze" cells, we can identify all cells that are reachable from the outside and thus will eventually lead out of the maze.
• Count the number of cells that can reach the exit. Subtract this number from the total number of cells in the maze to determine how many are part of loops (i.e., cells that cannot reach the exit).

意思大概就是从外部往内部能走到的都不能构成循环，剩下的，如果有单独的 ? 格子，四周都被不构成循环的格子围上了，那它也不构成循环格子。
其余所有，通过构造均能构成循环格子。

my code

#include<bits/stdc++.h>
#define L(i, j, k) for(int i = (j); i <= (k); ++i)
#define R(i, j, k) for(int i = (j); i >= (k); --i)
#define sz(a) ((int) (a).size())
#define pb emplace_back
#define me(a, x) memset(a, x, sizeof(a))
#define vi vector<int>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned int;
using i128 = __int128;
#define TEST 
#define TESTS int T; cin >> T; while(T--)
const int N = 1010;
using namespace std;
int n, m;
char maz3[N][N];
int vis[N][N]; // 可达的点
void Main() {
    L(i, 0, N-1) L(j, 0, N-1) vis[i][j] = 1;
	cin >> n >> m;
	L(i, 1, n) L(j, 1, m) vis[i][j] = 0;
	int sum = n * m;
	L(i, 1, n) L(j, 1, m) { // 输入迷宫
	    cin >> maz3[i][j];
	}
	queue<pair<int, int>> q;
	L(i, 1, n) {
	    // 从最左边这一排走
	    if(maz3[i][1] == 'L') q.push({i, 1});
	    // 从最右边这一排走
	    if(maz3[i][m] == 'R') q.push({i, m});
	}
	L(i, 1, m) { // 同理
	    if(maz3[1][i] == 'U') q.push({1, i});
	    if(maz3[n][i] == 'D') q.push({n, i});
	}
    while(!q.empty()) {
        pair<int, int> now = q.front(); q.pop();
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, 1, 0, -1};
        vis[now.first][now.second] = 1;
        L(i, 0, 3) {
            int x = now.first + dx[i];
            int y = now.second + dy[i];
            if(1 <= x and x <= n and 1 <= y and y <= m) {
                if(i == 0 and maz3[x][y] == 'D' and !vis[x][y]) 
                    q.push({x, y});
                else if(i == 1 and maz3[x][y] == 'L' and !vis[x][y]) 
                    q.push({x, y});
                else if(i == 2 and maz3[x][y] == 'U' and !vis[x][y]) 
                    q.push({x, y});
                else if(i == 3 and maz3[x][y] == 'R' and !vis[x][y]) 
                    q.push({x, y});
            }
        }
    }
    // L(i, 1, n) {
        // L(j, 1, m) cout << vis[i][j] << ' ';
        // cout << endl;
    // }
    L(i, 1, n) L(j, 1, m) {
        if(maz3[i][j] == '?' and 
        vis[i-1][j] == 1 and vis[i+1][j] == 1 and
        vis[i][j-1] == 1 and vis[i][j+1] == 1) vis[i][j] = 1;
    }
    L(i, 1, n) L(j, 1, m) if(vis[i][j] == 1) sum--;
    cout << sum << endl;
}
int main() {
	ios :: sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	TESTS Main();
	return 0;
}