Recommendations
Suppose you are working in some audio streaming service. The service has \(n\) active users and \(10^9\) tracks users can listen to. Users can like tracks and, based on likes, the service should recommend them new tracks.
Tracks are numbered from \(1\) to \(10^9\). It turned out that tracks the \(i\)-th user likes form a segment \([l_i, r_i]\).
Let's say that the user \(j\) is a predictor for user \(i\) (\(j \neq i\)) if user \(j\) likes all tracks the \(i\)-th user likes (and, possibly, some other tracks too).
Also, let's say that a track is strongly recommended for user \(i\) if the track is not liked by the \(i\)-th user yet, but it is liked by every predictor for the \(i\)-th user.
Calculate the number of strongly recommended tracks for each user \(i\). If a user doesn't have any predictors, then print \(0\) for that user.
Input
The first line contains one integer \(t\) (\(1 \le t \le 10^4\)) — the number of test cases. Next, \(t\) cases follow.
The first line of each test case contains one integer \(n\) (\(1 \le n \le 2 \cdot 10^5\)) — the number of users.
The next \(n\) lines contain two integers \(l_i\) and \(r_i\) per line (\(1 \le l_i \le r_i \le 10^9\)) — the segment of tracks the \(i\)-th user likes.
Additional constraint on the input: the sum of \(n\) over all test cases doesn't exceed \(2 \cdot 10^5\).
Output
For each test case, print \(n\) integers, where the \(i\)-th integer is the number of strongly recommended tracks for the \(i\)-th user (or \(0\), if that user doesn't have any predictors).
题义:
有 1000000000 首音乐, 名字是1,2,3,......等等,
然后有 n 个用户, 这些用户喜欢的音乐都是一个连续的区间,
定义一个用户的推荐人, 推荐人喜欢的音乐区间完全包含用户喜欢的音乐,
对于每一个用户, 求他的所有推荐人共同喜欢的音乐但用户不喜欢的音乐, 有多少
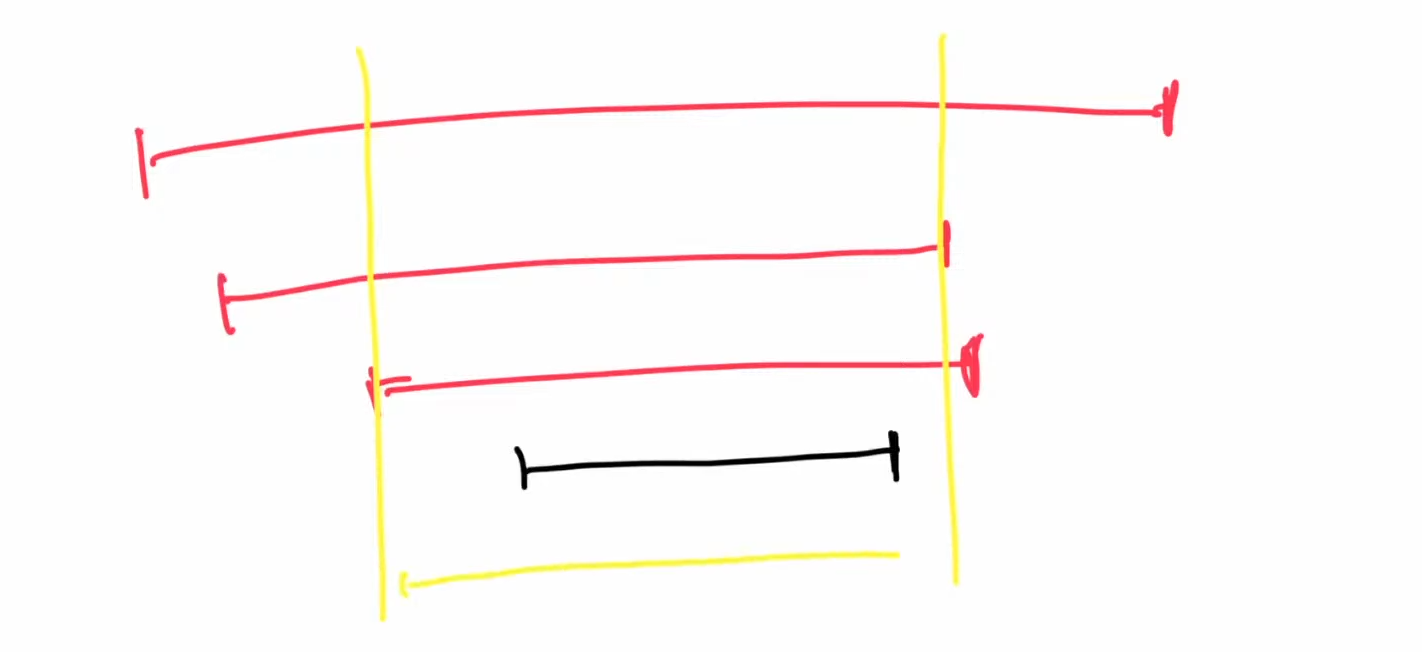
(对于这个图片, 答案是黄色区间减去黑色区间的个数)
先放上蒋老师的做法
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = (j); i <= (k); ++i)
#define R(i, j, k) for(int i = (j); i >= (k); --i)
#define sz(a) ((int) (a).size())
#define pb emplace_back
#define me(a, x) memset(a, x, sizeof(a))
#define vi vector<int>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned int;
using i128 = __int128;
#define TEST
#define TESTS int T; cin >> T; while(T--)
const int N = 1E+6;
using namespace std;
void Main() {
int n;
cin >> n;
vi l(n), r(n); // 所有用户的区间左右端点
L(i, 0, n-1) {
cin >> l[i];
cin >> r[i];
}
vi LL(n, -1), RR(n, -1); // 对于每一个用户, 他的推荐人并集区间的左右端点
vi p(n); // 排序用
iota(p.begin(), p.end(), 0);
{ // 先找每个用户的推荐人并集区间的右端点
sort(p.begin(), p.end(), [&](int i, int j){
if(l[i] != l[j]) { // 排序, 先把左端点在左边的放前面, 这样他之后的用户都可以被他左包围, 只需判断右边即可
return l[i] < l[j];
}
return r[i] > r[j]; // 如果左边一样, 那么区间长的放前面, 因为不这样的话, 区间长的用户不会被算作区间短的用户的推荐人
});
set<int> s; // 维护一个集合, 集合里的元素是排序后的在当前用户前面的用户的右端点, 这些用户的左端点在当前用户前面, 只要找到最小的并且大于当前用户的右端点, 当前用户的推荐人并集区间的右端点就找到了, 而其后面的由于左端点大于当前用户左端点, 必定不会是当前用户的推荐人
for(int j = 0; j < n; ++j) {
int i = p[j];
auto it = s.lower_bound(r[i]); // lower_bound函数返回 大于 等于 传参的第一个迭代器
if(it != s.end()) { // 如果能在左端点小于当前用户的用户里找到右端点最小的大于当前用户的右端点, 当前用户的推荐人并集区间的右端点就是右端点最小的大于当前用户的右端点
RR[i] = *it;
}
s.insert(r[i]); // 把当前判断过的用户的右端点放入集合
if(j + 1 < n and l[i] == l[p[j + 1]] and r[i] == r[p[j + 1]]) { // 特判, 如果当前用户的下一个和他完全一样, 那么他的下一个用户不会被算到当前用户的推荐人里
RR[i] = r[i]; // 如果下一个和他一样, 那么他的推荐人并集就是他本身, 对于连续的一样的用户, 最后一个显然答案也是正确的
}
}
}
{ // 这个跟上一个代码块同理
sort(p.begin(), p.end(), [&](int i, int j){
if(r[i] != r[j]) {
return r[i] > r[j];
}
return l[i] < l[j];
});
set<int> s;
for(int j = 0; j < n; ++j) {
int i = p[j];
auto it = s.upper_bound(l[i]); // 由于upper_bound函数返回 大于 传参的第一个迭代器
if(it != s.begin()) { // 所以如果不是第一个的话, 就有左端点比当前用户小的或者等于他的
LL[i] = *prev(it); // 当前迭代器的上一个的左端点一定小于等于当前用户
}
s.insert(l[i]);
if(j + 1 < n and l[i] == l[p[j + 1]] and r[i] == r[p[j + 1]]) {
LL[i] = l[i];
}
}
}
// L(i, 0, n-1) { // 检验代码
// cout << LL[i] << ' ' << RR[i] << endl;
// }
L(i, 0, n-1) {
int ans;
if(LL[i] == -1) { // 可以证明, 如果LL[i] == -1, 那么 RR[i] == -1
ans=0;
}
else {
ans = RR[i] - LL[i] - (r[i] - l[i]);
}
cout << ans << endl;
}
}
int main() {
ios :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
TESTS Main();
return 0;
}
我的复刻
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = (j); i <= (k); ++i)
#define R(i, j, k) for(int i = (j); i >= (k); --i)
#define sz(a) ((int) (a).size())
#define pb emplace_back
#define me(a, x) memset(a, x, sizeof(a))
#define vi vector<int>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned int;
using i128 = __int128;
#define TEST
#define TESTS int T; cin >> T; while(T--)
const int N = 1E+6;
using namespace std;
void Main() {
int n; cin >> n;
vi l(n), r(n);
L(i, 0, n-1) cin >> l[i] >> r[i];
vi LL(n, -1), RR(n, -1);
vi p(n); // p(n)定义了访问顺序
iota(p.begin(), p.end(), 0);
//sort(p.begin(), p.end(), [=](int a, int b){ // 这一行不能写 [=], 得写 [&], 不知道为什么
sort(p.begin(), p.end(), [&](int a, int b){
if(l[a] == l[b]) {
return r[a] > r[b];
}
return l[a] < l[b];
});
set<int> st;
st.clear();
L(j, 0, n-1) {
int i = p[j]; // 有这句话才能按顺序来
auto it = st.lower_bound(r[i]);
if(it != st.end()) {
RR[i] = *it;
}
st.insert(r[i]);
//if(i != n-1 and l[i] == l[i+1] and r[i] == r[i+1]) { // 这么写是错的
if(j < n - 1 and l[i] == l[p[j+1]] and r[i] == r[p[j+1]]) {
RR[i] = r[i];
//cout << "YES!!!" << endl;
}
}
//sort(p.begin(), p.end(), [=](int a, int b){
sort(p.begin(), p.end(), [&](int a, int b){
if(r[a] == r[b]) {
return l[a] < l[b];
}
return r[a] > r[b];
});
st.clear();
L(j, 0, n-1) {
int i = p[j];
auto it = st.upper_bound(l[i]);
if(it != st.begin()) {
LL[i] = *prev(it);
}
st.insert(l[i]);
//if(i != n-1 and l[i] == l[i+1] and r[i] == r[i+1]) {
if(j != n-1 and l[i] == l[p[j+1]] and r[i] == r[p[j+1]]) {
LL[i] = l[i];
//cout << "YES!!!" << endl;
}
}
// L(i, 0, n-1) {
// cout << LL[i] << ' ' << RR[i] << endl;
// }
L(i, 0, n-1) {
if(LL[i] != -1) {
cout << RR[i] - LL[i] - r[i] + l[i] << endl;
}
else {
cout << 0 << endl;
}
}
//cout << endl;
}
int main() {
ios :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
TESTS Main();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号