机器学习

机器学习

一、深度学习

1.1、绪论

人工智能、机器学习和深度学习的关系

人工智能 > 机器学习 > 深度学习

• 人工智能是一个目标，该目标是指实现机器能够像人一样思考，感知和推理
• 机器学习是实现人工智能的一种方法
• 深度学习只是使用了深度神经网络的机器学习

1.1.1、从专家系统到机器学习

• 专家系统：基于人工定义的规则
• 机器学习：基于人对问题的理解去提取特征，再将特征和结果建立映射关系，构造分类器

1.1.2、从传统机器学习到深度学习

传统机器学习：特征处理（数据预处理、特征提取、特征转换） + 浅层学习

深度学习：分层 + 组合 简单特征 - > 复杂特征

1.1.3、深度学习的能与不能

• 不能
  • 算法输出不稳定，容易被攻击
  • 模型复杂度高，难以纠错和调试
  • 模型层级复合程度高，参数不透明
  • 端到端训练方式对数据依赖性强，模型增量性差
  • 专注直观感知类问题，对开放性问题无能为力
  • 人类知识无法有效引入进行监督，机器偏见难以避免

1.2、深度学习概述

1.2.1、浅层神经网络

神经元特性：

• 多输入单输出：多树突接收多信号
• 空间和时间整合：不同位置的树突可在不同时间不同位置接收信号输入
• 输入分两种：兴奋性/抑制性
• 阈值特性：当信号输入量达到一定的阈值之后才会激活神经元

激活函数的两个参数：结点数和层数

激活函数的作用：完成输入到输出空间的变换

• 升维/降维
• 放大/缩小
• 旋转
• 平移
• 弯曲

增加神经网络层数：增加激活函数的次数，也就是增加非线性转换次数

多层神经网络可以看成是一个复合的非线性多元函数

瘦高还是矮胖？

瘦高代表着有着较高的神经网络层数但是每一层的节点数较少

矮胖代表着有着较低的神经网络层数但是每一层的节点数较多

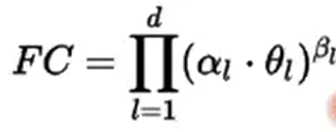
层数这一参数在指数上，理论上相同成本的情况下应该增加神经网络的层数

单层感知器：实现简单的与或非，解决线性问题

多层感知器的出现：单层感知器无法处理非线性分类问题（例如：异或），将单层感知器进行组合（异或的逻辑电路可以通与或非组合实现）

神经网络的参数学习：

• 梯度下降
• 误差反向传播

梯度和梯度下降：

• 梯度：多元函数中，一个点在各个方向都有导数，其中最大方向导数的方向就是梯度的方向，值就是梯度的值

• 误差反向传播：误差通过梯度传播，找到极小值点，反向传播回去，以极小值点作为初始值继续传播，直到找到最小值

• 前馈：某一层的输出作为上一层的输入

• 残差：损失函数在某个结点的偏导

梯度消失

增加深度会造成梯度消失，误差无法传播（某一层的训练结果较差，导致其他层无法更新训练数据）

1.2.2、神经网络到深度学习

逐层预训练：逐层进行训练，每次训练之前都以一个较好的参数值开始。

实现逐层预训练：

• 自编码器：对输入进行编码，通过中间层解码还原输入

• 受限玻尔兹曼机（RBM）：两层神经网络：可见层和隐藏层

二、pytorch基础

---

pyTorch是一个python库，它主要提供了两个高级功能：

• GPU加速的张量计算
• 构建在反向自动求导系统上的深度神经网络

1、pytorch基础代码练习

1.1、什么是张量？

张量（tensor）是数字各种形式的总称。

• 不同类型的数字：1、1.1...

• n维数组：[1,2,3]、[[1,2,3],[4,5,6]]...

1.2、定义张量

维度取决于深度

导包：

import torch

dtype的值：

• torch.float32
• torch.int32
• ...

定义不同张量：

#一个数
x = torch.tensor(1)
#一维数组,dtype 可指定数据类型
x = torch.tensor([1,2,3],dtype = torch.float)
#二维数组
x = torch.tensor([[1,2,3],[4,5,6]])
#全1张量，参数为每一个维度的长度(2行3列的二维数组，值为全1)
x = torch.ones(2,3)
#全0张量
x = torch.zeros(2,3)
#以一个张量的类型创建一个新的张量
y = x.new_zeros(2,3)
#空张量(数据的类型和值均随机)
x = torch.empty(2,3)
#随机初始化张量(值随机)
x = torch.rand(2,3)
# 利用原来的tensor的大小，但是重新定义了dtype
y = torch.randn_like(x, dtype=torch.float)

张量形状：

print(x.size())
print(x.shape)

1.3、定义操作

切片符：':'，左闭右开

#每一个维度的高度
m = torch.tensor([[2, 5, 3, 7],[4, 2, 1, 9]])
print(m.size(0),m.size(1),m.size(),sep='\n')
#返回元素的数量
print(m.numel())
#返回第0行，第2列的数
print(m[0][2])
# ','分割的是维度，':'对行或者列进行切片
#返回第1个维度中第1行的所有元素, 
print(m[1,:])
#返回第2个维度第1行的所有元素
print(m[:,1])
#三维
o = t.tensor([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print(o[0,0,:])
#tensor([1, 2, 3])
#标量积(结果为标量),要求两个张量的维度一致
v1 @ v2
#高纬度切片后进行内积，返回
m = t.tensor([1,3,4])
v = t.tensor([[1,4,3],[2,4,5],[3,4,5]])
print(v[[0],:] @ m)
#tensor([25])

from matplotlib import pyplot as plt

# matlabplotlib 只能显示numpy类型的数据，下面展示了转换数据类型，然后显示
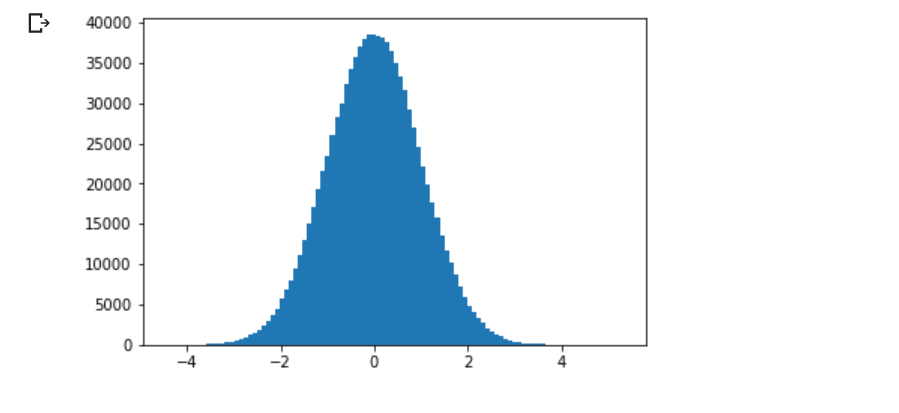
# 注意 randn 是生成均值为 0， 方差为 1 的随机数
plt.hist(t.randn(10**6).numpy(), 100);

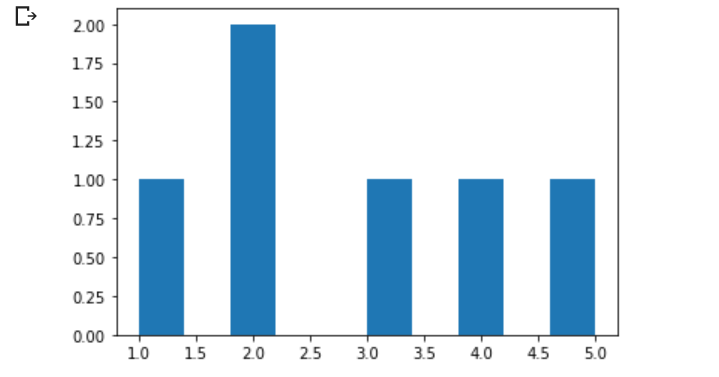
#在指定方向上的张量进行拼接
a = t.Tensor([1,2,3])
b = t.Tensor([2,4,5])
plt.hist(t.cat((a,b),0));

2、螺旋数据分类

绘图函数

!wget https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/plot_lib.py

引入基本的库，然后初始化重要参数

import random
import torch
from torch import nn, optim
import math
from IPython import display
from plot_lib import plot_data, plot_model, set_default

# 因为colab是支持GPU的，torch 将在 GPU 上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('device: ', device)

# 初始化随机数种子。神经网络的参数都是随机初始化的，
# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，
# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量

X：特征矩阵

Y：样本标签

X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
    index = 0
    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t
    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）
    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开
    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
    
    # 每个样本的(x,y)坐标都保存在 X 里
    # Y 里存储的是样本的类别，分别为 [0, 1, 2]
    for ix in range(N * c, N * (c + 1)):
        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
        Y[ix] = c
        index += 1

print("Shapes:")
print("X:", X.size())
print("Y:", Y.size())
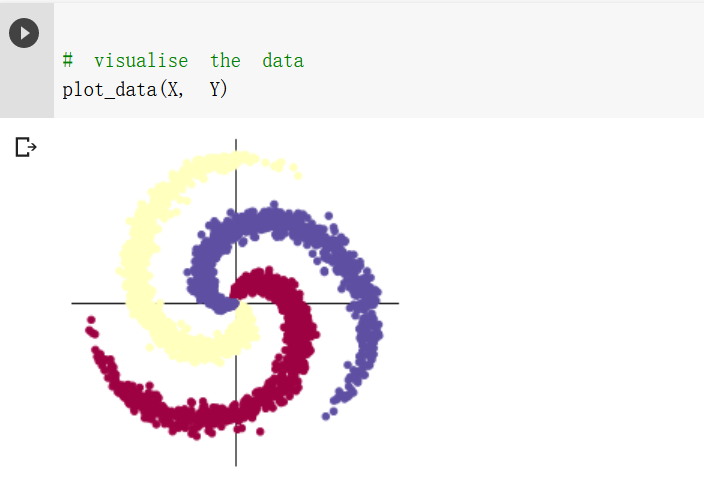
# visualise the data
plot_data(X, Y)

结果截图：

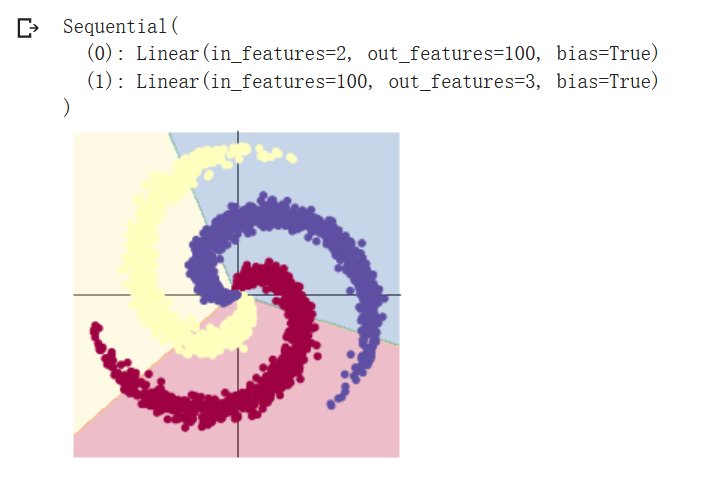
1、构建线性模型分类

learning_rate = 1e-3
lambda_l2 = 1e-5

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H),
    nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练
for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

    # 反向传播前把梯度置 0 
    optimizer.zero_grad()
    # 反向传播优化 
    loss.backward()
    # 更新全部参数
    optimizer.step()

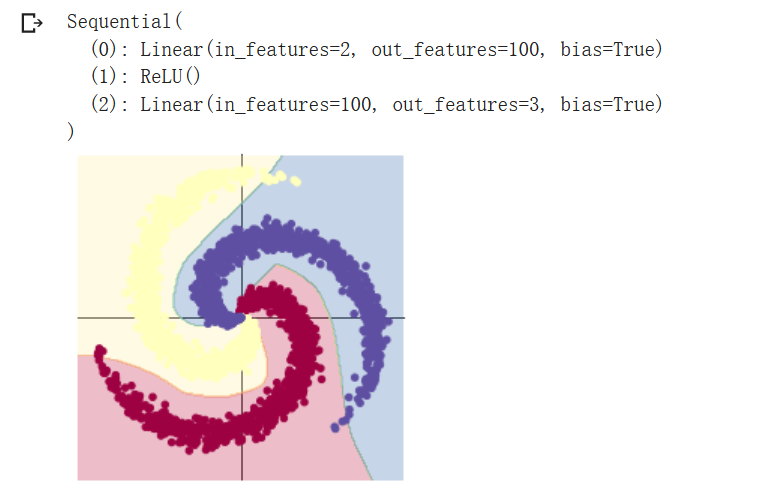
2、构建两层神经网络分类

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()
    
# Plot trained model
print(model)
plot_model(X, Y, model)
print(y_pred.shape)
print(y_pred[10, :])
print(score[10])
print(predicted[10])
# Plot trained model
print(model)
plot_model(X, Y, model)

output:

[EPOCH]: 999, [LOSS]: 0.873033, [ACCURACY]: 0.499
            torch.Size([3000, 3])
tensor([-0.1599, -0.1676, -0.1469], device='cuda:0', grad_fn=<slicebackward>)
tensor(-0.1469, device='cuda:0', grad_fn=<selectbackward>)
tensor(2, device='cuda:0')

2、构建两层神经网络分类

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()
# Plot trained model
print(model)
plot_model(X, Y, model)

output:

[EPOCH]: 999, [LOSS]: 0.168422, [ACCURACY]: 0.952