树状数组学习笔记

目录

1. 前言
2. 树状数组基础
   2.1 定义
   2.2 lowbit
   2.3 部分性质
   2.4 单点加，区间加，求前缀和
3. 树状数组求逆序对

---

1.前言

关于我线段树合并都会了还不懂树状数组这回事

2.树状数组基础

2.1 树状数组定义

众所周知，世界上有个东西叫线段树，维护的是一个区间。
它大概长这样：

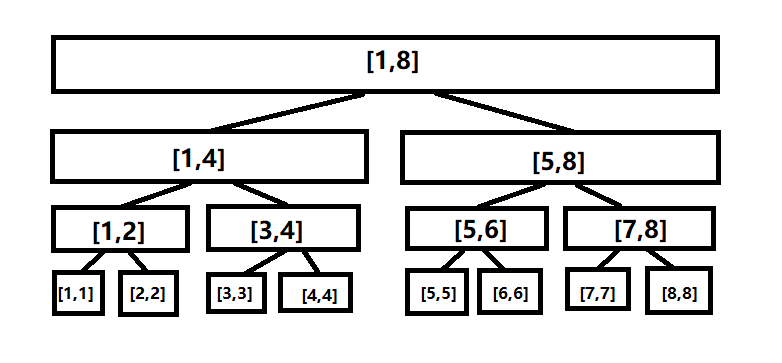
而把它移一下，就是树状数组

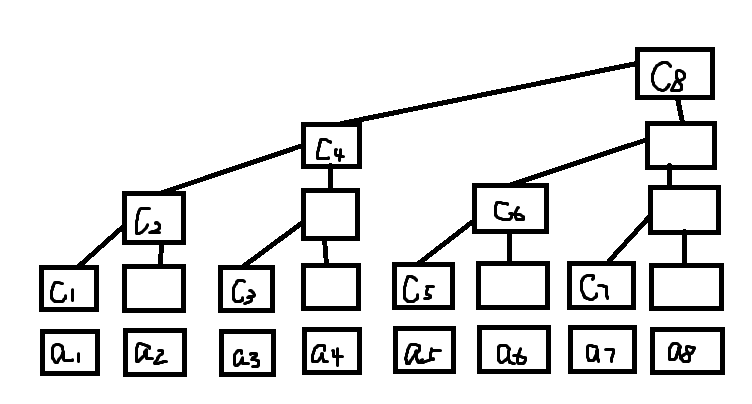
易得
\(c_1=a_1\)
\(c_2=a_1+a_2\)
\(c_3=a_3\)
\(c_4=a_1+a_2+a_3+a_4\)
\(......\)
这样看可能发现不了什么规律

2.2 lowbit

定义一个函数 \(f=lowbit(x)\) ，表示 \(x\) 在二进制表达式中最低位 \(1\) 所表示的数
举个例子：

\[(10)_2=1010 \]

最低位 \(1\) 在倒数第二位，所以

\[lowbit(10)=(10)_{10}=2 \]

所以易得：
设 \(k\) 为一个二进制数最低位 \(1\) 所在的位数，所以这个数的lowbit值即为 \(2^{k-1}\)
所以这个lowbit值可以用以下代码求：

int lowbit(int x)
{
    return x&(-x);
}

---

那么这个lowbit有什么用呢？
我们再把之前的树状数组搬过来
\(c_1=a_1\)
\(c_2=a_1+a_2\)
\(c_3=a_3\)
\(c_4=a_1+a_2+a_3+a_4\)
\(......\)
如果我们把下标变成2进制
\(c_{0001}=a_{0001}\)
\(c_{0010}=a_{0001}+a_{0010}\)
\(c_{0011}=a_{0011}\)
\(c_{0100}=a_{0001}+a_{0010}+a_{0011}+a_{0100}\)
\(......\)
令 \(k\) 为 \(i\) 在二进制表达式中最低位 \(1\) 所表示的数
不难发现：

\[c_i=a_{i-2^{k-1}+1}+a_{i-2^{k-1}+2}+...+a_i \]

即：

\[c_i=a_{i-lowbit(i)+1}+a_{i-lowbit(i)+2}+...+a_i \]

这就是 \(c\) 数组的规律

2.3 部分性质

1. \(c_x\) 保存以它为根的子树中所有叶节点的个数
2. \(c_x\) 的子节点个数为 \(lowbit(x)-1\)
3. 除树根外，\(c_x\) 的父节点为 \(c_{x+lowbit(x)}\)
4. 树的深度为 \(\text{log}\)\(_2n\)

2.4 单点加，区间加，区间查询

由于我们知道了 \(c_x\) 的子节点个数为 \(lowbit(x)-1\) 和 除树根外，\(c_x\) 的父节点为 \(c_{x+lowbit(x)}\) 这两个性质，所以以下的就很好理解了
单点加，区间查询
因为树状数组维护的是前缀和，所以一个点改变肯定会影响到它的父节点
我们知道 \(c_x\)的父节点是 \(c_{x+lowbit(x)}\) ,所以我们每次跳 \(lowbit(x)\) ，也就是跳到 \(x\) 的父节点，然后将它的值加上要加的值就可以了
而区间查询也很好解决，因为树状数组本来就是维护前缀和的，所以如果查询 \([x,y]\) 的和，就是查询 \([1,y]-[1,x-1]\)
代码：

int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int k)//单点加
{
	for(;x<=n;x+=lowbit(x))
		c[x]+=k;
}
int sum(int x)//区间查询
{
	int ans=0;
	for(;x;x-=lowbit)
		ans+=c[x];
	return ans;
}

区间加，单点查询
区间点加加上单点查询的话，我们的做法就不一样了。因为如果用之前的做法，那肯定会超时
所以我们就要用到差分的思想，利用差分建树
我们令 \(a[0]=0,b[i]=a[i]-a[i-1]\)
易得：

\[a[i]=\sum_{j=1}^i b[j] \]

我们很容易发现，如果有区间值改变，差值是不变的，只有 \(b[x]\) 和 \(b[y+1]\) 改变。所以我们可以用这个来建立树状数组
代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+7;
int c[N],a[N];
int n,m;
int lowbit(int x)
{
	return x&(-x);
}
int sum(int x)
{
	int ans=0;
	for(;x;x-=lowbit(x))
		ans+=c[x];
	return ans;
}
void add(int x,int k)
{
	for(;x<=n;x+=lowbit(x)) c[x]+=k;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	//	add(i,a[i]);
	}
	while(m--)
	{
		int op;
		cin>>op;
		if(op==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
			add(x,k);
			add(y+1,-k);
		}
		else
		{
			int x;
			cin>>x;
			cout<<sum(x)+a[x]<<endl;
		}	
	}
	return 0;
}

3.树状数组求逆序对

知道了树状数组的基础，树状数组求逆序对就很好理解了。
维护一个树状数组，记录每个数出现的次数，然后从后往前扫一遍数组，每次就在树状数组中查询有多少比它小的数，计入答案中，然后再将自己出现次数+1即可。
代码实现：

int ans=0;
for(int i=n;i>=1;i--)
{
	ans+=sum(a[i]-1);
	add(a[i],1);
}