前言
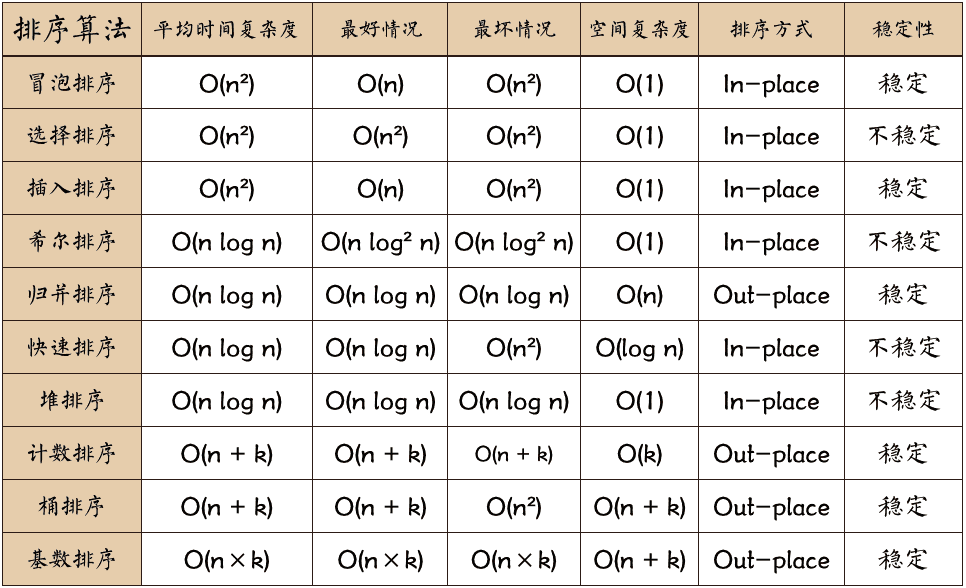
最近心血来潮,对十大排序算法做了一个简单性能测试对比,下图是一张理论性能对比图(已找不到出处)。尽管有些算法的时间复杂度一样,比如冒泡排序,选择排序和插入排序的平均时间复杂度都是 O(n^2),但是由于它们常数项不一样,使得它们实际性能差别很大。
测试说明
- windows 10系统
- i7-11700K@3.60GHz 64GB RAM
- 时间统计未区分 CPU 用户时间和 CPU 系统时间,时间仅为开始和结束时间差,忽略了系统调度带来的误差
- 比较交换统计代码未体现在下面给出的代码中,文末会附上完整代码
- 如有优化的,先单独测试,最后汇总对比
1. 冒泡排序 bubble
冒泡排序代码如下
void sort_bubble(std::vector<int> &arr) {
int length = arr.size();
for (int i = 0; i < length - 1; i++) {
for (int j = 0; j < length - i - 1; j++) { //轮询 length-1 次
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
冒泡排序的算法很简单,两个for循环,总的轮询次数和比较次数都是:(n-1) + (n-2) + ... + 1 = n*(n-1)/2。不论输入数据情况如何,顺序的,逆序的,部分顺序的,轮询和比较的次数一样多。
针对这些情况,可以对冒泡排序做一些优化,常用方法有三种:
- 外层循环优化:设置一个标记用于标记本次是否发生交互,如果本次轮询没有发生交换,说明待排序数组已经是顺序的,不需要再排序,直接退出即可
- 内层循环优化:记录最后一次发生数据交换的位置(数组下标),说明这个位置之后的数组都是有序的,下一次轮询只轮询到这个位置即可
- 双向冒泡排序:又称鸡尾酒排序(cocktail sort),向右轮询时将最大值往右边移,再向左轮询将最小值往左移
以下代码是集合了上述三种优化方法的代码
void sort_bubble2(std::vector<int> &arr) {
int length = arr.size();
int lastExchange = 0; //最后一次发生交换的位置
int left = 0, right = arr.size() - 1;
while (left < right) {
bool exchange = false;
for (int i = left; i < right; i++) { //往右轮询
if (arr[i] > arr[i + 1]) {
int temp = arr[i + 1];
arr[i + 1] = arr[i];
arr[i] = temp;
exchange = true;
lastExchange = i;
}
}
if (exchange == false) { //如果没有发生数据交换,说明数组已有序
return;
}
exchange = false;
right = lastExchange;
for (int i = right; i > left; i--) { //往左轮询
if (arr[i] < arr[i - 1]) {
int temp = arr[i - 1];
arr[i - 1] = arr[i];
arr[i] = temp;
exchange = true;
lastExchange = i;
}
}
if (exchange == false) {
return;
}
left = lastExchange;
}
}
测试对比:
| 数据长度 | 数据方式 | 排序算法 | 时间S | 比较次数 | 交换次数 | 排序算法 | 时间S | 比较次数 | 交换次数 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 顺序 逆序 随机[0-1000] 全0 0->max->1 |
sort_bubble | 0.004 0.011 0.009 0.004 0.008 |
499500 499500 499500 499500 499500 |
0 499500 248232 0 249001 |
sort_bubble2 | 0.000 0.011 0.007 0.000 0.006 |
999 499500 333797 999 332669 |
0 499500 248232 0 249001 |
|
| 10000 | 顺序 逆序 随机[0-10000] 全0 0->max->1 |
sort_bubble | 0.355 1.079 0.772 0.327 0.682 |
49995000 49995000 49995000 49995000 49995000 |
0 49995000 25022825 0 24990001 |
sort_bubble2 | 0.001 1.054 0.643 0.000 0.590 |
9999 49995000 33301272 9999 33326669 |
0 49995000 25022825 0 24990001 |
|
| 100000 | 顺序 逆序 随机[0-100000] 全0 0->max->1 |
sort_bubble | 32.537 103.080 77.567 32.879 69.141 |
4999950000 4999950000 4999950000 4999950000 4999950000 |
0 4999950000 2505074044 0 2499900001 |
sort_bubble2 | 0.001 104.881 64.226 0.001 58.965 |
99999 4999950000 3338285231 99999 33326669 |
0 4999950000 2505074044 0 2499900001 |
从数据可以看出
- 交换次数的多少直接影响bubble排序时间
- 冒泡排序效率很低,一百万的数据排序时间将超多3000秒,所以未测试
- 优化过的冒泡排序除了在顺序,全0(几乎不会发生这种情况)几乎不耗时外,在随机数组情况下,效率有小幅提升,但是不明显,约为
64.226/77.567 = 82.8% - 逆序情况下(几乎不会出现),算法优不优化,效果一样
2. 选择排序 selection
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
void sort_selection(std::vector<int>& arr) {
int length = arr.size();
for (int i = 0; i < length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < length; j++) { //对比查找最小值的索引
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) { //将最小值放到已排序序列末尾
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}
选择排序优化:每次遍历挑选出最小值和最大值,最小值放到左边有序序列末尾,最大值放到右边有序序列起始。这样便利次数会少一半。
void sort_selection2(std::vector<int>& arr) {
for (int left = 0, right = arr.size() - 1; left < right; left++, right--) {
int minIndex = left;
int maxIndex = right;
for (int i = left; i <= right; i++) {
if (arr[i] < arr[minIndex]) {
minIndex = i;
}
if (arr[i] > arr[maxIndex]) {
maxIndex = i;
}
}
if (minIndex != left) {
int temp = arr[left];
arr[left] = arr[minIndex];
arr[minIndex] = temp;
}
if (maxIndex == left) { //先交换left,需要考虑最大值就在left的情况
maxIndex = minIndex;
}
if (maxIndex != right) {
int temp = arr[right];
arr[right] = arr[maxIndex];
arr[maxIndex] = temp;
}
}
}
测试数据
| 数据长度 | 数据方式 | 排序算法 | 时间S | 比较次数 | 交换次数 | 排序算法 | 时间S | 比较次数 | 交换次数 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 顺序 逆序 随机[0-1000] 全0 0->max->1 |
sort_selection | 0.002 0.002 0.003 0.002 0.002 |
499500 499500 499500 499500 499500 |
0 500 996 0 995 |
sort_selection2 | 0.002 0.002 0.002 0.002 0.002 |
501000 501000 501000 501000 501000 |
0 500 991 0 991 |
|
| 10000 | 顺序 逆序 随机[0-10000] 全0 0->max->1 |
sort_selection | 0.236 0.256 0.246 0.228 0.238 |
49995000 49995000 49995000 49995000 49995000 |
0 5000 9991 0 9990 |
sort_selection2 | 0.277 0.233 0.221 0.215 0.225 |
5001000 5001000 5001000 5001000 5001000 |
0 5000 9985 0 9986 |
|
| 100000 | 顺序 逆序 随机[0-100000] 全0 0->max->1 |
sort_selection | 22.333 22.939 22.767 22.473 22.156 |
4999950000 4999950000 4999950000 4999950000 4999950000 |
0 50000 99992 0 99991 |
sort_selection2 | 21.705 22.738 21.593 21.793 22.403 |
5000100000 5000100000 5000100000 5000100000 5000100000 |
0 50000 99975 0 99981 |
- 输入数据情况对选择排序时间影响不大,排序时间只受数据量的影响
- 优化后效果不明显
3. 插入排序 insertion
void sort_insertion(std::vector<int>& arr) {
for (int i = 1; i < arr.size(); i++) {
int preIndex = i - 1;
int current = arr[i];
while (preIndex >= 0 && current < arr[preIndex]) {
arr[preIndex + 1] = arr[preIndex];
preIndex = preIndex - 1;
}
arr[preIndex + 1] = current;
}
}
优化思路1:前半部分已经完成排序是有序序列,则可以通过二分查找法,查找下一个数据的插入点,但是数据的移动个数没有变,可以尝试使用memcpy来代替轮询移动。
优化思路2:希尔排序
4. 希尔排序 shell
希尔排序,也被称为递减增量排序,是插入排序的一种改进版本。将插入排序对比交换间隔 1 改成 gap 就是希尔排序。
void sort_shell(std::vector<int>& arr) {
for (int gap = arr.size() / 2; gap > 0; gap = gap / 2) { //使用gap进行递减插入排序,当 gap == 1 时,完全是插入排序
for (int i = gap; i < arr.size(); i++) {
int preIndex = i - gap;
int current = arr[i];
while (preIndex >= 0 && current < arr[preIndex]) {
arr[preIndex + gap] = arr[preIndex];
preIndex = preIndex - gap;
}
arr[preIndex + gap] = current;
}
}
}
希尔排序的核心是gap序列的设置,我选取了几个gap序列测试,使用以下代码测试
static inline void sort_insertion_gap(std::vector<int>& arr, int gap) {
for (int i = gap; i < arr.size(); i++) {
int preIndex = i - gap;
int current = arr[i];
while (preIndex >= 0 && current < arr[preIndex]) {
arr[preIndex + gap] = arr[preIndex];
preIndex = preIndex - gap;
}
arr[preIndex + gap] = current;
}
}
void sort_shell_gap(std::vector<int>& arr, float divisor) {
int gap = 0;
for (gap = int(arr.size()*1.0 / divisor); gap > 0; gap = int(gap * 1.0 / divisor)) {
sort_insertion_gap(arr, gap);
}
if (gap != 1) {
sort_insertion_gap(arr, 1);
}
}
| 数据长度 | 数据方式 | 排序算法 | 时间S | 比较次数 | 交换次数 | 排序算法 | 时间S | 比较次数 | 交换次数 | 排序算法 | 时间S | 排序算法 | 时间S | 排序算法 | 时间S |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10000 | 顺序 逆序 随机[0-1000] 全0 0->max->1 |
sort_shell | 0.001 0.001 0.003 0.001 0.001 |
120005 172578 262568 120005 145769 |
0 62560 147599 0 30748 |
gap_2.2 | 0.001 0.001 0.002 0.001 0.001 |
110843 147003 205750 110843 143453 |
0 44816 100214 0 36788 |
gap_3 | 0.001 0.001 0.003 0.001 0.001 |
gap_4 | 0.000 0.002 0.003 0.000 0.001 |
gap_5 | 0.001 0.001 0.004 0.001 0.001 |
| 100000 | 顺序 逆序 随机[0-10000] 全0 0->max->1 |
sort_shell | 0.012 0.018 0.041 0.013 0.015 |
1500006 2244585 4244870 1500006 1849170 |
0 844560 2795529 0 399136 |
gap_2.2 | 0.011 0.015 0.034 0.012 0.016 |
1408345 1873314 2671875 1408345 1836048 |
0 551604 1317032 0 469577 |
gap_3 | 0.009 0.015 0.040 0.009 0.012 |
gap_4 | 0.007 0.015 0.041 0.007 0.012 |
gap_5 | 0.006 0.015 0.116 0.006 0.012 |
| 1000000 | 顺序 逆序 随机[0-100000] 全0 0->max->1 |
sort_shell | 0.160 0.216 0.611 0.148 0.183 |
18000007 26357530 68376922 18000007 22371988 |
0 9357504 50878221 0 4871952 |
gap_2.2 | 0.149 0.185 0.374 0.140 0.189 |
17083348 22856174 33672822 17083348 22421397 |
0 6639212 17120198 0 5756891 |
gap_3 | 0.107 0.185 0.527 0.102 0.149 |
gap_4 | 0.084 0.181 0.615 0.078 0.130 |
gap_5 | 0.073 0.179 3.561 0.071 0.129 |
| 10000000 | 顺序 逆序 随机[0-100000] 全0 0->max->1 |
sort_shell | 1.779 2.582 8.960 1.739 2.185 |
220000008 317626219 1069948411 220000008 270962910 |
0 107626176 854961948 0 55962560 |
gap_2.2 | 1.644 2.175 4.507 1.576 2.133 |
200833345 268000919 405669941 200833345 264788606 |
0 75831416 210155083 0 68143804 |
gap_3 | 1.183 2.093 9.045 1.146 1.668 |
gap_4 | 0.942 0.002 8.609 0.922 1.539 |
gap_5 | 0.883 2.112 39.075 0.861 1.555 |
- gap 的选择对排序算法效率影响很大
- 从这几个组测试数据来看,gap 选择 2.2 综合效率最高
5. 归并排序 merge
static inline void Merge(std::vector<int>& arr, int left, int mid, int right) {
int n = right - left + 1;//临时数组存合并后的有序序列
int* tmp = new int[n];
int k = 0;
int i = left;
int j = mid + 1;
while (i <= mid && j <= right) {
if (arr[i] < arr[j]) {
tmp[k++] = arr[i++];
}
else {
tmp[k++] = arr[j++];
}
}
while (i <= mid) {
tmp[k++] = arr[i++];
}
while (j <= right) {
tmp[k++] = arr[j++];
}
for (int m = 0; m < n; ++m) {
arr[left + m] = tmp[m];
}
delete[] tmp;//删掉堆区的内存
}
static inline void sortMerge(std::vector<int>& arr, int left, int right) {
if (left == right) {
return; //递归基是让数组中的每个数单独成为长度为1的区间
}
int mid = (left + right) / 2;
sortMerge(arr, left, mid);
sortMerge(arr, mid + 1, right);
Merge(arr, left, mid, right);
}
void sort_merge(std::vector<int>& arr) {
sortMerge(arr, 0, arr.size() - 1);
}
6. 快速排序 quick
static inline int partition(std::vector<int>& arr, int left, int right) {
int pivot = arr[left]; /* 在最左边挖了一个坑,并临时保存坑中的元素,此时left指向这个坑 */
while (left < right) {
while (left < right && arr[right] >= pivot) {
right--;
}
arr[left] = arr[right]; /* 从右往左,找到第一个小于基准的值,与坑进行互换 */
while (left < right && arr[left] <= pivot) {
left++;
}
arr[right] = arr[left]; /* 从左望右,找到第一个大于基数的值,与坑进行互换 */
}
arr[left] = pivot; /* 把基准填入最后一个坑 */
return left;
}
static inline void quickSort(std::vector<int>& arr, int left, int right) {
if (left >= right) {
return;
}
int position = partition(arr, left, right);
if (position > left) {
quickSort(arr, left, position - 1);
}
if (position < right) {
quickSort(arr, position + 1, right);
}
}
void sort_quick(std::vector<int>& arr) {
quickSort(arr, 0, arr.size() - 1);
}
以上代码的中函数 partition 中的 pivot 每次都选最左边的值,当数组是逆序或者大面积逆序的时候,效率很差。同时数据逆序时,递归调用层数太多,很有可能栈溢出。
稍微改动一点,每次在 left 和 right 中间选取一个随机位置,将这个位置与 left 进行交换,相当于 pivot 的值就是随机的,改动代码如下
static inline int partition_random(std::vector<int>& arr, int left, int right) {
std::default_random_engine random(time(NULL));
std::uniform_int_distribution<int> dis1(left, right);
int mid = dis1(random);
int temp = arr[left];
arr[left] = arr[mid];
arr[mid] = temp;
int pivot = arr[left]; /* 在最左边挖了一个坑,并临时保存坑中的元素,此时left指向这个坑 */
while (left < right) {
while (left < right && arr[right] >= pivot) {
right--;
}
arr[left] = arr[right]; /* 从右往左,找到第一个小于基准的值,与坑进行互换 */
while (left < right && arr[left] <= pivot) {
left++;
}
arr[right] = arr[left]; /* 从左望右,找到第一个大于基数的值,与坑进行互换 */
}
arr[left] = pivot; /* 把基准填入最后一个坑 */
return left;
}
经测试发现,在输入数组本身为随机的情况下,partition_random 方法效率要差很多,原因是随机函数调用次数太多导致性能差,于是做一点点改进,换成使用获取ns时间来模拟随机值
static inline int partition_random_time(std::vector<int>& arr, int left, int right) {
uint64_t t = std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count();
int mid = t % (right - left) + left;
int temp = arr[left];
arr[left] = arr[mid];
arr[mid] = temp;
int pivot = arr[left]; /* 在最左边挖了一个坑,并临时保存坑中的元素,此时left指向这个坑 */
while (left < right) {
while (left < right && arr[right] >= pivot) {
right--;
}
arr[left] = arr[right]; /* 从右往左,找到第一个小于基准的值,与坑进行互换 */
while (left < right && arr[left] <= pivot) {
left++;
}
arr[right] = arr[left]; /* 从左望右,找到第一个大于基数的值,与坑进行互换 */
}
arr[left] = pivot; /* 把基准填入最后一个坑 */
return left;
}
测试对比
| 数据长度 | 数据方式 | 排序算法 | 时间S | 比较次数 | 交换次数 | 栈深 | 排序算法 | 时间S | 比较次数 | 交换次数 | 栈深 | 排序算法 | 时间S | 比较次数 | 交换次数 | 栈深 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10000 | 顺序 逆序 全0 0->max->1 随机[0-10000] 随机[0-1000] 随机[0-100] 随机[0-10] |
sort_quick | 0.167 0.148 0.165 0.002 0.002 0.001 0.003 0.013 |
49995000 50000000 49995000 477279 201426 225631 539491 4156165 |
9999 9999 9999 30955 31227 28140 22158 14680 |
199980 199980 199980 1640 580 900 3140 24980 |
sort_quick_random | 0.022 0.018 0.192 0.020 0.022 0.026 0.030 0.039 |
173230 177047 49995000 211550 206076 212510 536657 4243287 |
6718 12773 9999 32612 31089 28787 22346 14904 |
620 600 199980 600 640 800 3220 23720 |
sort_quick_random_time | 0.001 0.001 0.150 0.002 0.001 0.001 0.002 0.015 |
159219 178019 49995000 209432 199248 230973 547243 4532485 |
7062 12540 9999 31622 31438 28148 21936 14724 |
580 640 199980 660 560 1000 3200 25240 |
| 100000 | 顺序 逆序 全0 0->max->1 随机[0-100000] 随机[0-10000] 随机[0-1000] 随机[0-100] |
sort_quick | 14.959 14.654 15.479 0.026 0.019 0.016 0.025 0.125 |
4999950000 5000000000 4999950000 7622561 2681076 2762938 6020716 41162538 |
99999 99999 99999 391120 389278 364649 299146 222137 |
1999980 1999980 1999980 3060 780 940 3520 30380 |
sort_quick_random | 0.183 0.202 14.375 0.197 0.199 0.232 0.260 0.362 |
2018329 2226212 4999950000 2603392 2714558 2827954 5985350 41224175 |
62102 129462 99999 384938 385797 362389 299000 225317 |
680 760 1999980 720 900 1000 3700 29180 |
sort_quick_random_time | 0.010 0.010 14.099 0.016 0.020 0.019 0.029 0.133 |
2034893 2252728 4999950000 2697028 2662789 2816588 6031719 43824040 |
70760 124837 99999 402245 389422 362149 297201 215492 |
780 840 1999980 780 760 1000 3460 30680 |
| 1000000 | 顺序 逆序 全0 0->max->1 随机[0-1000000] 随机[0-100000] 随机[0-10000] 随机[0-1000] |
sort_quick | -1.000 -1.000 -1.000 0.368 0.200 0.201 0.289 1.346 |
0 0 0 109786135 33897189 34206626 66110991 430278258 |
0 0 0 4576789 4614226 4403201 3728938 2975141 |
0 0 0 4980 1100 1160 3740 28400 |
sort_quick_random | 1.712 2.023 -1.000 2.055 2.102 2.455 2.781 3.842 |
24297024 26128503 0 33585568 32921333 35084119 65943225 428986214 |
587196 1210851 0 4782607 4639564 4351762 3751578 2973398 |
920 960 0 980 1000 1280 3840 31240 |
sort_quick_random_time | 0.113 0.123 -1.000 0.176 0.228 0.231 0.306 1.330 |
24855857 26576833 0 33544634 33142889 34799692 65457491 426499334 |
706298 1250884 0 4687857 4636489 4377918 3761835 3003727 |
1000 980 0 1080 1000 1160 3760 30080 |
- 时间 -1.000 表示未测试,时间太长了,等不起
- 栈深度单位是4字节,有些许误差,但不会太大
- 使用随机pivot效果明显,在有序和部分有序情况对改善排序时间和递归栈深度都有改善
7. 堆排序 heap
static inline void heapify(std::vector<int>& arr, int i, int length) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < length && arr[left] > arr[largest]) {
largest = left;
}
if (right < length && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
heapify(arr, largest, length);
}
}
void sort_heap(std::vector<int>& arr) {
/* 构建大顶堆 */
for (int i = arr.size() / 2 - 1; i >= 0; i--) {
heapify(arr, i, arr.size());
}
for (int i = arr.size() - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapify(arr, 0, i);
}
}
8. 计数排序 counting
计数排序的思想是:对每一个输入元素x,确定小于x的元素个数,利用这一信息,就可以直接把x放到它在输出数组中的位置上了。
void sort_counting(std::vector<int>& arr) {
int max = arr[0];
for (int i = 0; i < arr.size(); i++) {
if (arr[i] > max) {
max = arr[i];
}
}
std::vector<int> count(max + 1, 0);
std::vector<int> tArr(arr);
for (auto x : arr) {
count[x]++;
}
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
for (int i = arr.size() - 1; i >= 0; i--) {
arr[count[tArr[i]] - 1] = tArr[i];
count[tArr[i]]--;
}
}
9. 桶排序 bucket
void sort_bucket(std::vector<int>& arr) {
int max = arr[0];
int min = arr[0];
for (int i = 0; i < arr.size(); i++) {
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < min) {
min = arr[i];
}
}
int bucketCount = 10;
int bucketSize = arr.size();
int gap = (max - min) / bucketCount + 1;
std::vector<std::vector<int>> bucket(bucketCount + 1);
for (int i = 0; i < arr.size(); i++) {
int index = (arr[i] / gap);
bucket[index].push_back(arr[i]);
}
int k = 0;
for (int i = 0; i < bucket.size(); i++) {
sort_shell(bucket[i]); //调用希尔排序
for (int j = 0; j < bucket[i].size(); j++) {
arr[k++] = bucket[i][j];
}
}
}
10. 基数排序 radix
void sort_radix(std::vector<int>& arr) {
/* 获取位数 */
int max = arr[0];
for (int i = 0; i < arr.size(); i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int d = 1;
int p = 10;
while (max >= p) {
max /= p;
d++;
}
std::vector<int> temp(arr.size(), 0);
std::vector<int> count(p);
for (int radix = 1, i = 0; i <= d; i++, radix *= p) {
for (int j = 0; j < p; j++) { /* 清空计数器 */
count[j] = 0;
}
for (int j = 0; j < arr.size(); j++) { /* 统计每个桶中的记录 */
int index = (arr[j] / radix) % p;
count[index]++;
}
for (int j = 1; j < p; j++) {
count[j] = count[j] + count[j - 1];
}
for (int j = arr.size() - 1; j >= 0; j--) {
int index = (arr[j] / radix) % p;
temp[count[index] - 1] = arr[j];
count[index]--;
}
for (int j = 0; j < arr.size(); j++) {
arr[j] = temp[j];
}
}
}
十大排序测试对比
- 测试耗时单位是秒
- 冒泡排序使用 sort_bubble2, 希尔排序使用 sort_shell_gap_2.2, 快速排序使用 sort_quick_random_time
| 数据长度 | 数据方式 | bubble | selection | insertion | shell | merge | quick | heap | counting | bucket | radix |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10000 万 |
顺序 逆序 全0 0->max->1 随机[0-10000] 随机[0-1000] 随机[0-100] 随机[0-10] |
0.000 0.684 0.000 0.343 0.403 0.393 0.393 0.383 |
0.237 0.250 0.233 0.227 0.228 0.230 0.227 0.225 |
0.000 0.360 0.000 0.164 0.163 0.161 0.161 0.147 |
0.001 0.001 0.001 0.001 0.003 0.002 0.001 0.002 |
0.003 0.003 0.003 0.003 0.003 0.003 0.003 0.003 |
0.001 0.001 0.142 0.001 0.002 0.002 0.002 0.012 |
0.004 0.004 0.001 0.003 0.004 0.004 0.004 0.003 |
0.000 0.000 0.000 0.001 0.000 0.000 0.000 0.000 |
0.001 0.001 0.002 0.001 0.003 0.002 0.002 0.001 |
0.001 0.002 0.000 0.001 0.001 0.001 0.001 0.001 |
| 100000 十万 |
顺序 逆序 全0 0->max->1 随机[0-100000] 随机[0-10000] 随机[0-1000] 随机[0-100] |
0.001 61.222 0.001 33.859 39.825 39.829 39.564 43.278 |
22.599 23.436 22.225 23.018 22.535 22.526 22.863 23.781 |
0.001 32.724 0.001 16.201 16.158 16.257 17.074 16.449 |
0.011 0.015 0.012 0.017 0.030 0.027 0.026 0.020 |
0.028 0.028 0.028 0.030 0.037 0.038 0.038 0.036 |
0.010 0.011 14.263 0.016 0.019 0.019 0.028 0.133 |
0.046 0.042 0.004 0.046 0.049 0.047 0.050 0.049 |
0.002 0.002 0.001 0.002 0.002 0.002 0.002 0.001 |
0.015 0.019 0.017 0.017 0.031 0.028 0.027 0.021 |
0.013 0.015 0.004 0.013 0.015 0.012 0.011 0.009 |
| 1000000 百万 |
顺序 逆序 全0 0->max->1 随机[0-1000000] 随机[0-100000] 随机[0-10000] 随机[0-1000] |
- - - - - - - - |
- - - - - - - - |
- - - - - - - - |
0.142 0.183 0.142 0.182 0.383 0.363 0.324 0.275 |
0.324 0.306 0.308 0.311 0.414 0.416 0.405 0.393 |
0.117 0.125 - 0.178 0.221 0.224 0.311 1.331 |
0.579 0.551 0.038 0.581 0.630 0.640 0.623 0.598 |
0.025 0.023 0.018 0.021 0.033 0.022 0.019 0.018 |
0.176 0.235 0.200 0.207 0.462 0.449 0.410 0.300 |
0.150 0.175 0.046 0.154 0.171 0.151 0.127 0.111 |
| 10000000 千万 |
顺序 逆序 全0 0->max->1 随机[0-10000000] 随机[0-1000000] 随机[0-100000] 随机[0-10000] |
- - - - - - - - |
- - - - - - - - |
- - - - - - - - |
1.600 2.139 1.609 2.127 4.542 4.398 4.005 3.499 |
3.375 3.342 3.350 3.354 4.628 4.604 4.514 4.391 |
1.310 1.373 - 2.030 2.562 2.588 3.459 13.738 |
6.910 6.637 0.363 6.972 9.015 9.015 8.941 9.001 |
0.251 0.237 0.181 0.212 0.886 0.303 0.232 0.197 |
2.011 2.669 2.329 2.366 6.426 6.201 5.962 5.135 |
1.746 1.945 0.463 1.725 1.723 1.717 1.515 1.316 |
| 100000000 亿 |
顺序 逆序 全0 0->max->1 随机[0-100000000] 随机[0-10000000] 随机[0-1000000] 随机[0-100000] |
- - - - - - - - |
- - - - - - - - |
- - - - - - - - |
17.698 23.631 17.656 23.425 52.693 51.197 47.068 41.920 |
36.396 36.297 36.145 36.865 51.035 50.766 49.950 48.687 |
14.377 14.977 - 22.245 28.941 29.133 37.513 142.467 |
80.115 77.762 3.617 81.797 143.594 136.161 137.860 131.183 |
2.521 2.323 1.832 2.140 10.130 8.420 3.221 2.612 |
23.266 30.549 25.508 27.192 95.108 93.309 90.055 80.646 |
19.521 21.508 4.673 19.327 21.460 19.427 17.248 15.114 |
- bubble,selection,insertion 三兄弟在决赛刚开始没多久就骂骂咧咧的退出了比赛
- 使用递减 gap 序列插入排序的希尔排序,表现很亮眼
- 归并排序时间复杂度,只与输入数据量大小有关,与数据是否有序关系不大
- 快速排序在输入序列值相同较多的情况下,时间复杂度高,输入全0也出现了退赛情况
- 堆排序
- 计数排序,桶排序,基数排序都很快,但是内存需求也很高,在可以使用空间换时间的情况下,是不错的选择
- 选择使用什么排序算法需要根据待排序数据情况做合适的取舍




 浙公网安备 33010602011771号
浙公网安备 33010602011771号