【OI 档案-2025】CSP 赛前集训记（初赛后+复赛）

复赛前 - 第一周（9.22 ~ 9.28）

Day1 - 周一

斌斌感冒了 awa，这天只能晚自习坐大牢了。

Day2 - 周二

直接来模拟赛吗 0.0，直接从 lzm 搬运吗？有点意思，但是被薄纱，155pts，rk5，没救了。

小梦学习计网

枚举+模拟，lzm 标黄题，实际顶多评红，但是被薄纱，某人对自己的位运算太自信了。但是确实很简单，没啥好讲的。

小梦的跳跃游戏

依旧被薄纱，难绷，破环成链 + 分层图最短路，但是不会，连破环成链都忘了，知道是最短路，但是不会建图，两个月没复习图论不行了。
破环成链后，由于每多往后面访问一个节点，权重多一，就可以分层建图，给每个节点连条边权为一的边，再给原点的连回一条无权边，就可以得到答案。

T3 和 T4 没写，T3 骗了分，但是因为不可以总司令输出 YES，唉。

自主留下来补题，补出来了会把记录补上，但是懒得贴代码了，这会导致篇幅过长。

Day3 - 周三

这周都是模拟赛。

P1931 套利

就是 SPFA 找正环嘛0.0，怎么评的绿？

UVA1400 "Ray, Pass me the dishes!"

区间合并，静态求区间最大子段和最左子区间，就……区间合并线段树呗……没啥好讲的，但是半小时出正解，调错一小时……

Day4 - 周四

斌斌说这把模拟赛貌似是最接近今年 \(S\) 的一把。

归去来兮女士的旅行（red）

T1 感觉可以评黄。
对凭证排序，然后枚举每个凭证要求低于 \(i\) 的子图，跑 floyd 求最短路即可。

下北泽大天使的树上染色（yellow）

T2 就上位绿/蓝吗 qwq
先对颜色离散化，然后离线处理，把每个操作（查询和修改）都打到对应的节点上，遍历树，枚举到的节点处理修改和查询。
修改操作用若干个单调栈和 BIT 维护，每个颜色对应的单调栈记录每个颜色被染上时间戳（操作），维护单调递减。如果栈为空或栈内存储的时间戳比当前的大，当前操作的时间戳为 \(l\) 设栈顶为 \(r\)（若栈为空则以操作数即操作时间戳末尾为 \(r\)），则时间戳区间 [l , r - 1] 内的所有查询的颜色总数加一，BIT 维护区间修单点查即可。注意查询时候需特判查询传参的颜色是否被染上，如果未被染上，则答案加一，判断方法与更新单调栈一致。回溯时需回溯，令单调栈与 BIT 做反操作即可。
首 \(A\) 是窝滴，但是不明白为啥没几个入敲暴力……

后面的题没看 awa，一蓝一紫……

下大雨了，和斌斌肩并肩（蹭伞）。

中间莫名其妙段了。

10-28

Day 几不知道了。由于被强制做记录故重新启动。

DNA 序列（DNA）

哈希题啊，但是忘了怎么写哈希了 qwq，所以……

思路大概就是维护一个长度为 \(k\) 的四进制数，类似于一个滑动窗口，就是除以 \(4\) 后加上右边新加的数乘上 \(4^k\)，就可以得到其对应的哈希值，取模嘛……就需要逆元了，所以就自然溢出了（不是，自然溢出带除法也不太对吧……），然后统计出现次数最多的就过了。

小奇采药(medicine)

0-1 背包板子？但是背包容量 \(\le 10^9\)，所以这道题是玄学。

咳咳，对于这道题目，我们只能搜索，由于数据随机，所以……启发式搜索神力！

直接 A* 就干完了。

估价函数长这样：

inline long long f(long long t, long long v) {
    long long h = 0;
    for (int i = t + 1 ; i <= n ; i++) {
        if (v >= a[i].c){
            v -= a[i].c;
            h += a[i].v;
        }
        else return (long long)(h + v * a[i].cost);
    }
    return h;
}

脑洞治疗仪 (brainhole)

区间合并线段树裸题啊……

本题要求维护最长连续 \(0\)，但和最大子段和类似。

维护最大子段和：

1、最大子段和合并：

有三种情况，如图：

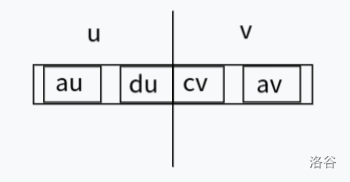
对这三种情况取最大值就是合并后的最大子段和，查询时的合并是将最大后缀和合并，分类讨论判断是否需要同 LCA 一同合并，如果需要，可将两个最大后缀和与 \(0\) 取最大值，因为 LCA 可以选择不之合并。

2、区间和合并：
直接将两个区间和相加即可。

3、最大前缀和合并：
有两种情况，第一种最大前缀和就是 \(c_u\)，第二种是 \(b_u+c_v\)，然后对两种情况取最大值。

4、最大后缀和合并：
同最大前缀和合并一样，有两种情况，第一种是 \(d_v\)，第二种是 \(b_v+d_u\)，对两种情况取最大值即可。

综上可以得出：
\(a_f=\max(c_v+d_u,a_u,a_v),b_f=b_u+b_v,c_f=\max(c_u,b_u+c_v),d_f=\max(d_v,b_v+d_u)\)。

然后我们在分别维护区间 \(0\) 的数量，就可以得到区间长度。

在合并是特判区间长度是否等于前后缀最大值，就可以得到最大连续长度。

然后维护区间赋值、区间求和、区间最长连续 \(0\) 即可

至于填补，线段树上二分找到操作边界进行赋值即可。

然后就干完了。

洗衣服(clothes)

贪心签到题，我们先处理洗衣机，用小根堆维护最小完成时间，求得每件衣服洗完的时间。然后处理烘干机，同样用一个小根堆维护最小完成时间，求得每件衣服烘干的时间。然后显然的一点，洗完的时间越晚，其期望烘干的时间就应该越快，所以小配大即可。

逗号播撒机(comma)

把字符串离散成整型，然后用带权并查集维护两个字符串在数据中是否存在相邻逗号，最后特殊处理打印即可。

地下城市(city)

Tarjan 跑一遍点双求出有点双连通分量，然后遍历每一个分量，统计分量中割点数量，若割点数量为一，那么选择方案数为分量大小减一（排除割点）；反正如果大于一，那么就不需要建出口了，贡献为零。如果没有割点，即该图为点双连通图，方案数就为 \(C_2^n\)，然后就干完了。

锦标赛 (tournament)

按能力值升序排序，求得每种元素的差值，从后往前遍历，对于差值小于 \(K\) 的玩家都是可能胜利的玩家。

幸运数 (lucky)

用队列加链表维护，先遍历序列把第一轮选中的 \(i\) 入队，然后遍历一遍队列算一遍贡献，算完后再遍历一遍在链表上进行删除，并查看删除后是否可以组成新的 47，把它们入队。重复以上操作直到队列为空为止。

序列 (seq)

可以求出 \(a_i\) 变为 \(b_i\) 的操作数 \(c_i\)，组成序列 \(c\)，将其转化为差分数组，目标是将其清零，直接贪心消除正负对应的差分数组即可。

01 串 (binary)

不难发现 \(2^i \bmod 3\) 中，若 \(i\bmod 2 = 0\)，\(2^i \bmod 3=1\)；反之，\(2^i \bmod 3=2\)，所以就可以分讨，写出如下逆天的代码，分讨的思路看代码应该很容易看出来。

Code

if(n == 1 || ((n & 1) && (m <= 1))) {
	printf("-1 \n-1 \n");
	continue;
} else if(m == 0) {
	for(int i = 1 ; i <= n ; i ++) printf("1");
	printf("\n");
	for(int i = 1 ; i <= n ; i ++) printf("1");
	printf("\n");
	continue;
}
int now = p[n + m - 1];
n --;
if(now == 1) {
	if(n & 1) {
		printf("1");
		for(int i = 1 ; i < n ; i ++) printf("1");
		printf("10");
		for(int i = 1 ; i < m ; i ++) printf("0");
		printf("\n");	
		printf("1");
		if(m & 1) {
			for(int i = 1 ; i < m ; i ++) printf("0");
			printf("10");
			for(int i = 1 ; i < n ; i ++) printf("1");
			printf("\n");					
		} else {
			for(int i = 1 ; i < m ; i ++) printf("0");
			printf("01");
			for(int i = 1 ; i < n ; i ++) printf("1");
			printf("\n");					
		}
	} else {
		printf("1");
		for(int i = 2 ; i < n ; i ++) printf("1");
		printf("0101");
		for(int i = 2 ; i < m ; i ++) printf("0");
		printf("\n");		
		printf("1");
		if(m & 1) {
			for(int i = 2 ; i < m ; i ++) printf("0");
			printf("1010");
			for(int i = 2 ; i < n ; i ++) printf("1");
			printf("\n");					
		} else {
			for(int i = 2 ; i < m ; i ++) printf("0");
			printf("0101");
			for(int i = 2 ; i < n ; i ++) printf("1");
			printf("\n");					
		}
	}
} else {
	if(n & 1) {
		printf("1");
		for(int i = 1 ; i < n ; i ++) printf("1");
		printf("10");
		for(int i = 1 ; i < m ; i ++) printf("0");
		printf("\n");					
		printf("1");
		if(m & 1) {
			for(int i = 1 ; i < m ; i ++) printf("0");
			printf("10");
			for(int i = 1 ; i < n ; i ++) printf("1");
			printf("\n");					
		} else {
			for(int i = 1 ; i < m ; i ++) printf("0");
			printf("01");
			for(int i = 1 ; i < n ; i ++) printf("1");
			printf("\n");					
		}
	} else {
		printf("1");
		for(int i = 2 ; i < n ; i ++) printf("1");
		printf("0101");
		for(int i = 2 ; i < m ; i ++) printf("0");
		printf("\n");					
		printf("1");
		if(m & 1) {
			for(int i = 2 ; i < m ; i ++) printf("0");
			printf("1010");
			for(int i = 2 ; i < n ; i ++) printf("1");
			printf("\n");					
		} else {
			for(int i = 2 ; i < m ; i ++) printf("0");
			printf("0101");
			for(int i = 2 ; i < n ; i ++) printf("1");
			printf("\n");					
		}
	}
}