【OI 档案-2025】六月周记

6.7

上午，作业写了一半后开始摸鱼。

13:00 吃​完饭，无聊看班级群，发现是周日下午六点返校，作业丢一边，入营测试改到明天，先打今天的 Div2 吧。

13::50 小眯一觉后起床，开始准备打月赛。

14:00 开赛：

秒点 T1，一眼签到题，目测入门级，考线段相交。

14:20 完了，线段相交板子出锅啦！等等，线段相交板子不是入门级啊？高估此题了？

14:32 经过分析数学性质 A 掉了此题。

这就是我调了半小时的入门级代码：

for(int i = 2 ; i <= n ; i ++) 
  if(y[i - 1] < s[i - 1]) h += (y[i] >= s[i]) | (s[i] <= y[i]);
  else h += (s[i] >= y[i]) | (y[i] <= s[i]);

排到 400+，原地下跪。

接下来看 T2，浪费一个小时为了追求线性的 DP 做法一直碰壁（不是，DS 优化打满了怎么连样例都过不了？），结果发现正解是二分……不是，这 10%5E6%20 的数据范围不就是要求线性吗？

15:27 AC……前缀和+二分查找，应该是道提高-

极品代码：

in(n) , in(t);
for(int i = 1 ; i <= n ; i ++) in(d[i]);
sort(d + 1 , d + n + 1);
for(int i = 1 ; i <= n ; i ++) {
	c[i] = c[i - 1] + d[i];
	s[i] = s[i - 1] + d[i] * (i - 1);
	dp[i] = i * c[i] - s[i];
}
while(t --) {
	int t;
	in(t);
	if(t >= dp[n])cout<<n<<'\n';
	else if(t < dp[1])puts("0");
	else {
		cout<<upper_bound(dp + 1 , dp + n + 1 , t) - dp - 1<<'\n';
	}
}

排到 388 (bushi

看 T3 吧……

一眼树形 DP，但是不会，链状的线性做法也不会，甚至连暴力都没敲出来，原地下跪。

目光转向菊花图。

17:13 成功拿下菊花图的 18 分，排名达到 78，逆天改命。

代码：

for(auto u : v[0]) {
	if(vis[u]) {
		ans += r[u];
		for(auto to : v[u]) {
			if(!vis[to])continue;
			ans += min(r[to] , t[to]);
		}
	} else {
		int h1 = r[u] , h2 = 0;
		for(auto to : v[u]) {
			if(!vis[to])continue;
			h1 += min(r[to] , t[to]) , h2 += r[to];
		}
		ans += min(h1 , h2);
	}
}

想 T4 暴力，虽然知道是组合数学或数论，但是无能为力，没学啊。dfs 挂飞，光荣爆零。

最终：100 + 100 + 18 + 0 = 218

排行：99/1653

应该不会掉分qwq

6.8

去北京集训营的入营测试，没过就只能老实待长沙回炉重造了……

7:45 吃完饭开始准备工作。

8:12 正式开打。

瞪 T1 感觉写过类似的，但不记得了，半小时搓了个伪贪心结果过了大样例，但小样例没过，离谱。

9:08 思索 DP 做法，然后花近一个小时写了个 \(n\sqrt{n}\) 的 DP，算了一下感觉可以拿 45 分，交了。

9:58 开始康 T2，最大区间 mex？随手搓了个带修莫队，发现写错了，调了半天调不出来，寄。

10:30 转战到分块，但是结局一样。

11:00 放弃了，开始敲暴力，BIT 二分双 log 暴力求区间 mex，然后双指针爆扫。

11:27 完成暴力，交。

11:32 中场休息后康 T3，发现可以状压，但是不会，磕了几分钟后果断放弃，开始敲暴力……

暴力持续出锅，修修修，高级修机工上线。

12:30 过样例，交。

T4 懒得看，反正不会，检查代码。

目测题目难度：省选-、省选-、省选、省选。

12:42 比赛结束。

0 + 0 + 12 + 0 = 12 ？？？

什么情况？前两题怎么会爆0？丸辣，只能待在长沙了qwq

12:50 向家人汇报战况……没有被批？哦，原来还有一场啊，那没事了。

生地会考考完后再打吧，希望不要太难……

为啥入营考直接上 NOIP 难度？是冲 NOIP 高分的吗？我 S1 都还没拿呢qwq，又要被史莱姆嘲讽了qwq。

八下校队期末测试（2025-6-13）

校队第二学期的期末测试，主要考了数位 DP 和状压 DP。由于对对数位 DP 掌握不牢，赛时把状压的题全写了，但数位的题只写了一道，第二天把题全补了。

比赛难度配置：黄-蓝-蓝-蓝-蓝

_感觉良好。

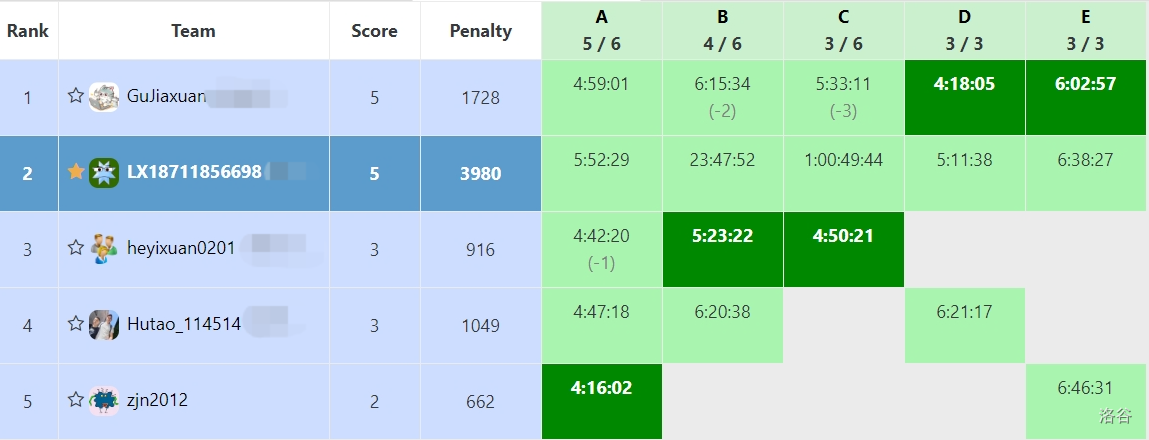
一道首 \(A\) 都没有，菜死了。

T1：CF244B Undoubtedly Lucky Numbers

签到题，记忆化搜索直接暴力搜就行，涉及一丢丢数位 DP 的思想。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (1 << 10) - 1;
ll ans = 0;
map<ll , ll>mp;
void dfs(int n , ll m , int x , int y) {
	//cout<<x<<','<<y<<','<<m<<'\n';
	if(m > n) return;
	if(m && !mp[m])ans ++;
    mp[m] = 1;
	if(x || m)dfs(n , m * 10 + x , x , y);
	dfs(n , m * 10 + y , x , y);
}
int main() {
	int n;
	cin>>n;
	for(int i = 0 ; i <= 9 ; i ++) 
		for(int j = i + 1 ; j <= 9 ; j ++) 
            dfs(n , 0 , i , j);
	cout<<ans;
	return 0;
}

T2：CF628D Magic Numbers

分别对奇数位于偶数位做分类讨论，偶数只能选 \(d\)，奇数位不能选 \(d\)，只对满足要求的位进行搜索，组合完所有的数位后，要判断该数是否整除 \(m\)，在搜索的过程中维护余数，看最后余数是否为 \(0\)。
\(l,r\) 的范围很大，懒得敲高精减，直接用 \(r-l\) 然后再单独算 \(l\) 的贡献。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e3 + 5 , mod = 1e9 + 7;
int dp[2005][2005] , m , d , num[2005] , top;
int dfs(int n , int x , int y , int tag) {
	if(x > n) return !y;
	if(~dp[x][y] && !tag) return dp[x][y];
	int h = 0;
	for(int i = 0 ; i <= (tag ? num[x] : 9) ; i ++)
		if(x & 1) {
			if(i != d) h = (h + dfs(n , x + 1 , (y * 10 + i) % m , tag && (i == num[x]))) % mod;
		} else if(i == d) {
			h = (h + dfs(n , x + 1 , (y * 10 + i) % m , tag && (i == num[x]))) % mod;
		}
	if(!tag) dp[x][y] = h;
	return h;
}
int solve(string x) {
	int len = x.size();
	for(int i = 0 ; i < len ; i ++) num[i + 1] = x[i] - '0';
	return dfs(len , 1 , 0 , 1);
}
int check(string x) { 
    int h = 0 , len = x.size();
    for (int i = 0 ; i < len ; i ++) {
        int y = x[i] - '0';
        if (((i + 1) & 1) && y == d) return 0; 
        else if (!((i + 1) & 1) && y!=d) return 0; 
        h = (h * 10 + y) % m;
    }
    return h == 0;
}
signed main() {
	memset(dp , -1 , sizeof(dp));
	string l , r;
	cin>>m>>d>>l>>r;
	
	cout<<(solve(r) - solve(l) + check(l) + mod) % mod<<'\n';
	return 0;
}

T3：CF855E Salazar Slytherin's Locket

比较复杂的一道题，细节较多，需特判前导零和上界限制，还涉及一点转态压缩的思想。数位的上界限制需要转化为 \(b\) 进制，用一个状态压缩的数，其每一位表示对应数字出现的次数的奇偶性，所以可以直接用异或和来维护奇偶性。

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N = 70;
int num[N];
int dp[11][N][2005][2]; 

int dfs(int pos , int sum , int limit , int p , int b) {
    if (pos == 0) return !sum && p;
    if (!limit && ~dp[b][pos][sum][p]) return dp[b][pos][sum][p];
    int res = 0 , n = limit ? num[pos] : (b - 1);
    for (int d = 0; d <= n; d ++) {
        int now = p || d;
        res += dfs(pos - 1 , sum ^ (now ? (1 << d) : 0) , limit && (d == n) , now , b);
    }
    if (!limit) dp[b][pos][sum][p] = res;
    return res;
}
int solve(int n, int b) {
    int tot = 0;
    while (n) {
        num[++ tot] = n % b;
        n /= b;
    }
    return dfs(tot , 0 , 1 , 0 , b);
}
signed main() {
    memset(dp , -1 , sizeof(dp));
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int q;
    cin >> q;
    while (q--) {
        int b, l, r;
        cin >> b >> l >> r;
        int ans = solve(r , b) - solve(l - 1 , b);
        cout << ans << '\n';
    }
    return 0;
}

T4：[SCOI2005] 互不侵犯

一道比较好写的状压，居然有人打表过了%%%。
二维平面涉及行和列，只压缩行，当前的行由先前求出的行转移二来，通过为运算判断是否有相邻的位，对合法的状态算贡献。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (1 << 10) - 1;
ll dp[11][110][N + 5] , ans;
int n , K;
int gets(int x) {
	int h = 0;
	while(x) {
		h += x & 1;
		x >>= 1;
	}
	return h;
}
int main(){
	cin >> n >> K;
	dp[0][0][0] = 1;
	int NN = (1 << n) - 1; 
	for(int i = 1 ; i <= n ; i ++) {
		for(int j = 0 ; j <= K ; j ++) {
			for(int k = 0 ; k <= NN ; k ++) {
				int h = gets(k);
				if(h <= j && (k & (k >> 1)) == 0)
				for(int l = 0 ; l <= NN ; l ++) {
					if((k & l) == 0 && ((k >> 1) & l) == 0 && ((k << 1) & l) == 0 && ((l & (l >> 1)) == 0))
					dp[i][j][k] += dp[i - 1][j - h][l];
				}
			}
		}
	}
	for(int i = 0 ; i <= NN ; i ++) ans += dp[n][K][i];
	cout<<ans;
	return 0;
}

T5：[USACO06NOV] Corn Fields G

和 T4 很像，只是由八字变为了十字，还需考虑包含的关系，位运算通通搞定。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (1 << 12) - 1 , mod = 1e8;
ll dp[13][N + 5] , ans , a[13];
int n , m;
int main() {
	cin >> n >> m;
	for(int i = 1 ; i <= n ; i ++)
		for(int j = 1 ; j <= m ; j ++) {
			int x;
			cin>>x;
			a[i] <<= 1;
			a[i] |= x;
		}
	int NN = (1 << m) - 1;
	for(int i = 0 ; i <= NN ; i ++) if((i | a[1]) == a[1] && (i & (i >> 1)) == 0)dp[1][i] = 1;
	for(int i = 2 ; i <= n ; i ++) {
		for(int k = 0 ; k <= NN ; k ++) {
			if((k | a[i]) == a[i] && (k & (k >> 1)) == 0){
				//dp[i][k] = 1;
				for(int l = 0 ; l <= NN ; l ++) {
					if((k & l) == 0  && ((l | a[i - 1]) == a[i - 1]) && (l & (l >> 1)) == 0)
						dp[i][k] += dp[i - 1][l];
						dp[i][k] %= mod;
				}
			}
		}
	}
	for(int i = 0 ; i <= NN ; i ++) ans += dp[n][i] , ans %= mod;
	cout<<ans;
	return 0;
}

Last

要复习生地和准备期末考了，这个月暂时不搞 OI 了。
暑假放假第 \(4\) 天就要被抓回学校，\(7\) 月份全没了qwq。