55 链表中环的入口结点

题目要求:给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

思路一: Floyd环判定算法

使用fastptr和sloeptr两个速度不相同的指针,一旦它们两个进入链表中的环,就肯定会相遇

时间复杂度O(n)

空间复杂度O(1)

错误代码:没有看清楚题目啊?不是让你判断链表是否有环,而是要让你找到环的入口节点啊

 

public class Solution {
    public ListNode EntryNodeOfLoop(ListNode pHead){
        //考虑特殊情况
        if(pHead == null || pHead.next==null|| pHead.next.next==null) return null;
        //定义两个pointer
        ListNode fastptr = pHead;//快指针走两步
        ListNode slowptr = pHead;//慢指针走一步
        while( fastptr.next.next!=null && slowptr.next!=null){
            fastptr = fastptr.next.next;
            slowptr = slowptr.next;
            if(fastptr == slowptr) return fastptr;
        }
        return null;
    }
}

 

正确代码: 

25行的break语句,一定要放进if的{}中去,否则无法通过

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public ListNode EntryNodeOfLoop(ListNode pHead){
        //考虑特殊情况
        if(pHead == null || pHead.next==null|| pHead.next.next==null) return null;
        //定义两个pointer,和环是否存在的真假
        ListNode fastptr = pHead;//快指针走两步
        ListNode slowptr = pHead;//慢指针走一步
        boolean isExist = false;
        //判断环是否存在
        while( fastptr.next.next!=null && slowptr.next!=null){
            fastptr = fastptr.next.next;
            slowptr = slowptr.next;
            if(fastptr == slowptr){
                isExist = true;
                break;
            }
        }
        if(isExist == true){//环存在,找到环的入口节点
            slowptr = pHead; //只初始化其中一个指针,另外一个指针不动
            while(slowptr!= fastptr){
                fastptr = fastptr.next; //每个指针各走一步
                slowptr = slowptr.next; //每个指针各走一步
            }
            return slowptr;
        }
        return null; //环不存在,返回null
    }
}

 思路二:利用HashMap

这个方法完全不用分成 判断环存在+找到入口 两个步骤

遍历整个链表,如果节点在hashmap中已经存在,那么它肯定就是环的入口啊

时间复杂度O(n)

空间复杂度O(n)

import java.util.HashMap;
public class Solution {
    public ListNode EntryNodeOfLoop(ListNode pHead)
    {
        HashMap<Integer,Integer> hs=new HashMap<>();
        while(pHead!=null){
            if(!hs.containsKey(pHead.val)){
                hs.put(pHead.val,1);
            }else{
                return pHead;
            }
            pHead=pHead.next;
        }
        return null;
    }
}

 思路一的证明

链接：https://www.nowcoder.com/questionTerminal/253d2c59ec3e4bc68da16833f79a38e4
来源：牛客网

两个结论：

1、设置快慢指针，假如有环，他们最后一定相遇。

2、两个指针分别从链表头和相遇点继续出发，每次走一步，最后一定相遇与环入口。

证明1：设置快慢指针fast和low，fast每次走两步，low每次走一步。假如有环，两者一定会相遇（因为low一旦进环，可看作fast在后面追赶low的过程，每次两者都接近一步，最后一定能追上）。

证明2：

设：

链表头到环入口长度为--a

环入口到相遇点长度为--b

相遇点到环入口长度为--c

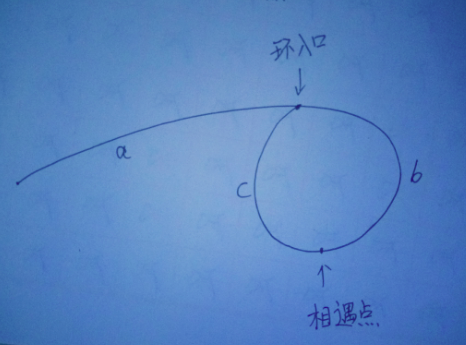
则：相遇时

快指针路程=a+(b+c)k+b ，k>=1  其中b+c为环的长度，k为绕环的圈数（k>=1,即最少一圈，不能是0圈，不然和慢指针走的一样长，矛盾）。

慢指针路程=a+b

快指针走的路程是慢指针的两倍，所以： //这一步我不太明白,作为备注

（a+b）*2=a+(b+c)k+b

化简可得：

a=(k-1)(b+c)+c 这个式子的意思是： 链表头到环入口的距离=相遇点到环入口的距离+（k-1）圈环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发，最后一定相遇于环入口。