2025 IMO 学习笔记

P1

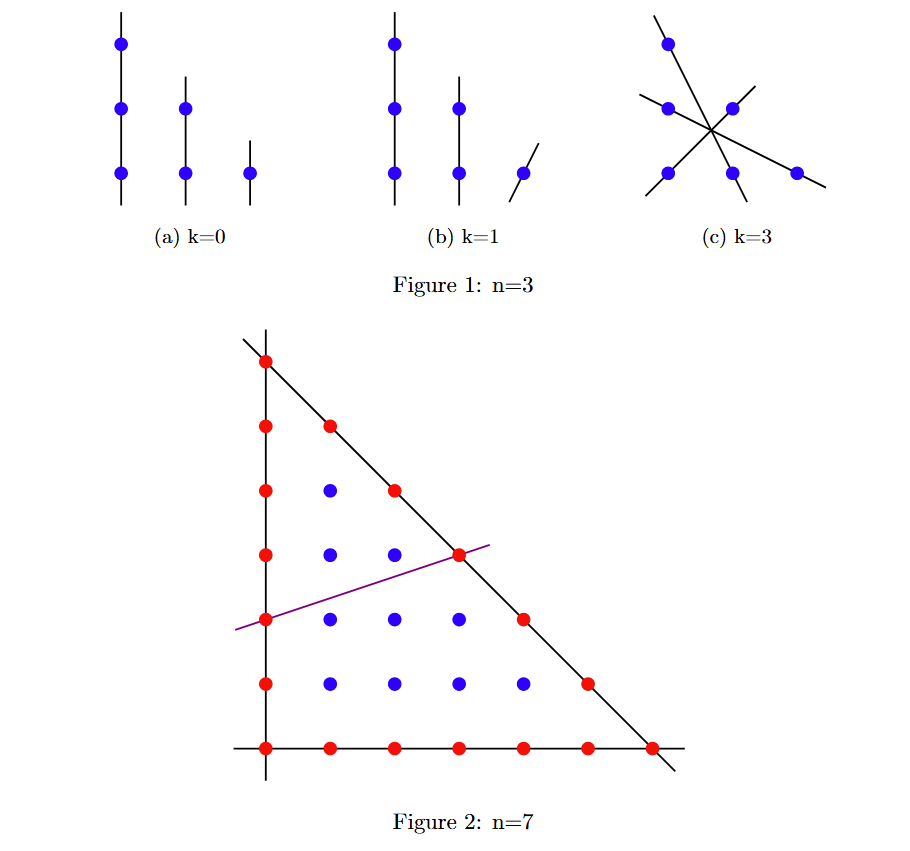
当 \(n=3\)，Figure 1，有 \(k=0,1,3\)，经枚举可知当一条为非阳光时，剩下两条一定要么都阳光要么都不，所以 \(k\ne 2\)。

当 \(n>3\)，Figure 2，若三条黑线（非阳光）至少选了一条，则可以将这一条线删去变成 \(n-1\) 规模的问题。否则，每条线最多经过两个红点，至少需要 \(\dfrac{3n-3}{2}>n\) 条线，无解。

所以 \(k=0,1,3\)。

P4

我们可以用 \((x,y,z)\) 来表示 \(n\) 的信息，其中 \(1<x<y<z\) 为 \(n\) 三个最小非 \(1\) 因子。

设 \(f(n)=\dfrac 1x+\dfrac 1y+\dfrac 1z\)，则 \(a_{i+1}=a_if(a_i)\)。

记 \(\nu_p(x)\) 为正有理数 \(x\) 中 \(p\) 因子的个数（可以为负）。

Lemma 1. \(a_i\) 是偶数。

Proof.

如果 \(a_i\) 是奇数，则 \(f(a_i)<1\implies a_{i+1}<a_i\) 且 \(a_{i+1}=a_if(a_i)\) 也为奇数（i.e. 三个奇数相加）。

\(a_i>a_{i+1}>a_{i+2}>\dots\)，无法成为无穷正整数序列。

Lemma 2. \(a_i\) 必须是 \(3\) 的倍数。

Proof.

\(a_i\) 从小到大归纳证明。

由 Lemma 1 知 \(a_i\) 是偶数。若待证命题不成立，即 \(3\nmid a_i\)，则 \(a_i\) 为 \((2,p,q),(2,p,2p),(2,4,p),(2,4,8)\)（\(p,q\) 为素数）之一。

• \((2,p,q)\)，有 \(f(a_i)=\dfrac{pq+2(p+q)}{2pq},\nu_2(f(a_i))=-1\)，\(a_{i+1}\) 为奇数，与 Lemma 1 矛盾。
• \((2,p,2p)\)，有 \(p\ne 3,f(a_i)=\dfrac{p+3}{2p}<1,\nu_3(f(a_i))=0\)，归纳。
• \((2,4,p)\)，有 \(f(a_i)=\dfrac{3p+4}{4p}<1,\nu_3(f(a_i))=0\)，归纳。
• \((2,4,8)\)，有 \(f(a_i)=\dfrac 78<1,\nu_3(f(a_i))=0\)，归纳。

Lemma 3. \(a_i\) 不是 \(5\) 的倍数。

Proof.

\(\nu_2(a_i)\) 从小到大归纳证明。

若是，则由于 Lemma 1,2 可知 \(a_i\) 为 \((2,3,4),(2,3,5)\) 之一。

• \((2,3,4)\)，有 \(f(a_i)=\dfrac {13}{12},\nu_2(f(a_i))=-2,\nu_5(f(a_i))=0\)，归纳。
• \((2,3,5)\)，有 \(f(a_i)=\dfrac {31}{30},\nu_2(f(a_i))=-1\)，\(a_{i+1}\) 为奇数，与 Lemma 1 矛盾。

---

所以对于满足 Lemma 1,2,3 的 \(a_i\)：

• \(\nu_2(a_i)\ge 2\)，即 \(a_i\) 为 \((2,3,4)\)，则 \(f(a_i)=\dfrac {13}{12},\nu_2(f(a_i))=-2,\nu_3(f(a_i))=-1,\nu_5(f(a_i))=0\)。
• \(\nu_2(a_i)=1\)，即 \(a_i\) 为 \((2,3,6)\)，则 \(f(a_i)=1\)。

所以可以再根据 \(\nu_2(a_i)\) 从小到大归纳，得到 \(a_1=12^k\cdot 6\cdot t\)，其中 \(k\in\mathbb N,t\in \mathbb N^+,2\nmid t,5\nmid t\)。

P6

Reference

设 \(n=45\)，我们解决规模为 \(n^2\times n^2\) 的问题。

将未覆盖的格子看成排列，即若 \((x,y)\) 未覆盖，则 \(p_x=y\)。

首先有结论 \(\{p\}\) 的 LIS 和 LDS 长度（分别设为 \(a,b\)）乘积不小于 \(n\)。而且 LIS 和 LDS 必然恰好有一个公共元素，设其为 \(O\)。

然后将所有格子按照其与 LIS、LDS 与 \(O\) 的相对位置染色其边界，如图：

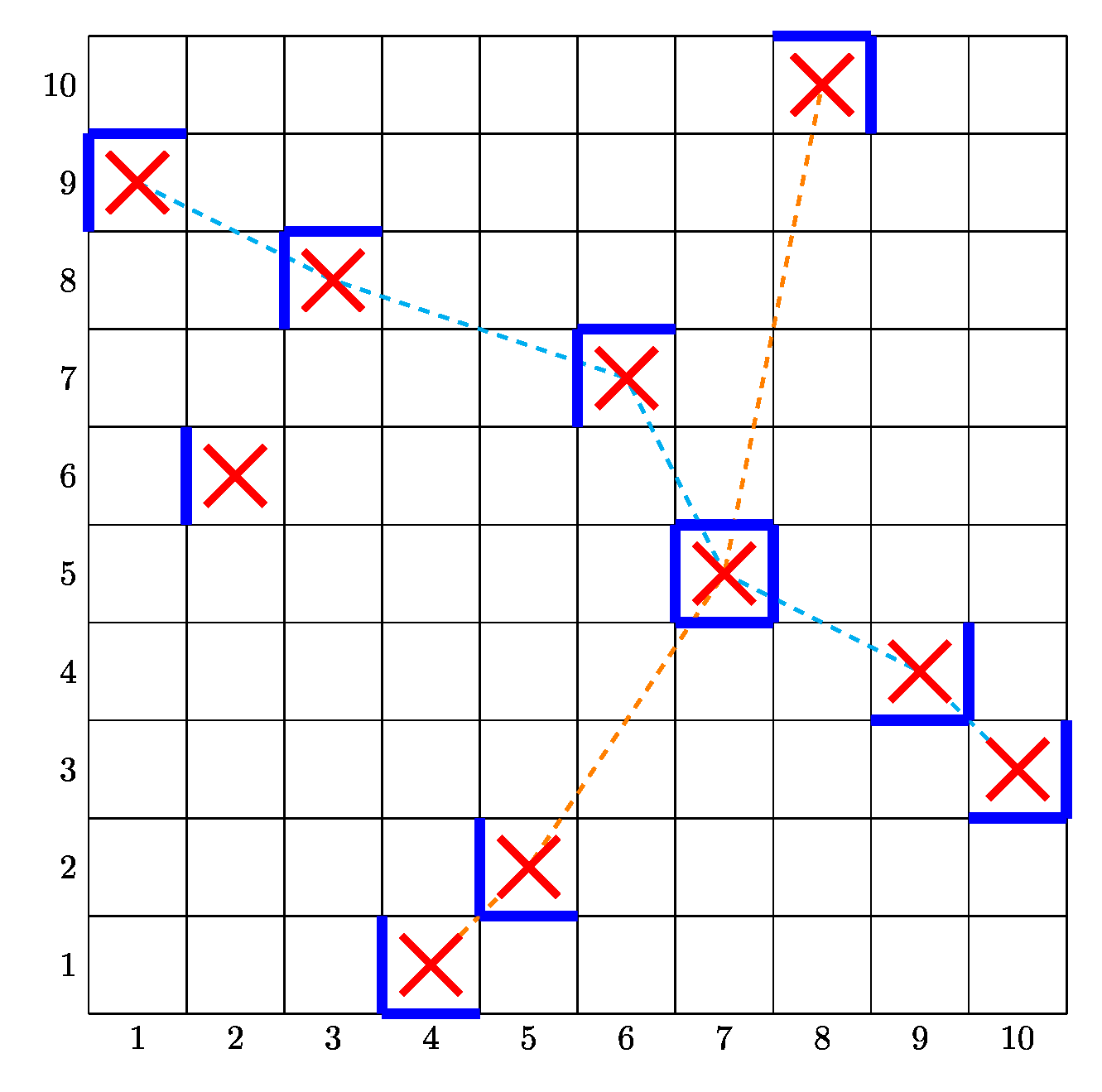
（有谁来教我 LaTeX 配色怎样好看）

注意到每个 tile 的边界最多碰到一个蓝色边，而且除了边界上最多四个蓝色边，其余都需要 tile 碰到它。

蓝色边个数为 \(n^2+a+b+1\)。

Tile 下界为 \(n^2+a+b-3\)。

由于 \(ab\ge n\)，取 \(a=b=n\) 得最小值，为 \(n^2+n+n-3=(n+1)^2-4\)。

构造很美妙，这里偷一张图：