树的中心重心直径一些特殊的东西

中心

所有直径的中点。

所以中点可能是一条边。

重心

最大的子树最小的点。

（“子树”都是指无根树的子树，即包括“向上”的那棵子树，并且不包括整棵树自身。）

• 以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。

• 树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。

• 把两棵树通过一条边相连得到一棵新的树，那么新的树的重心在连接原来两棵树的重心的路径上。

• 在一棵树上添加或删除一个叶子，那么它的重心最多只移动一条边的距离。

直径

树上任意两节点之间最长的简单路径。

求法为两遍 DFS。

推论：

\((u,v)\) 为树的直径，当且仅当 \(u\) 是 \(v\) 的最远点，且 \(v\) 是 \(u\) 的最远点。

一棵树可以有多条直径，在多条直径之间有以下结论：

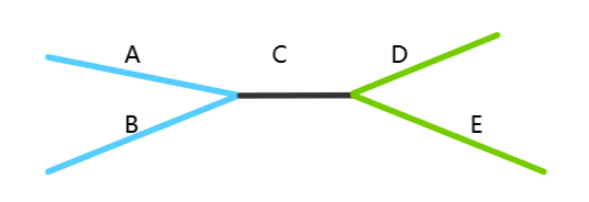
任意两条直径必然有公共点，且长这样：

其中 \(A=B,D=E,A+C\ge D,D+C\ge A\)。

进一步

对于任意一点 \(x\)，\(x\) 距最远点 \(d\) 距离。

则任意一条直径 \((s,t)\)，\(dis(s,x)=d \lor dis(t,x)=d\)。

总结

遇最远点/最长距离，考虑直径。

遇直径/距离和，考虑重心/中心。

“研究距离，考虑直径” “研究直径，考虑中心”