2-sat

P4782 【模板】2-SAT 问题

record

是啥

给定一些 bool 变量，和一些形如「某 bool 为 true/false 则另一个 bool 必然为 true/false」的条件，问是否有解（并构造）。

构图

将 \(n\) 个 bool 变量拆成 \(2n\) 个点，分别表示某 bool 取 true/false 的情况。

首先我们要知道条件 \(p,q\)：

\[(p\implies q)\iff (\neg q\implies \neg p) \]

所以假设我们有条件「\(a_1\) 若为 true，则 \(a_2\) 为 false」，则我们这样连边：

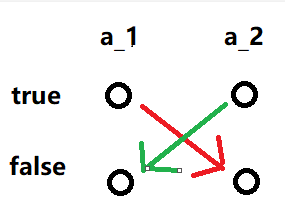
其中绿色边代表逆否命题。

所以我们就得到了一个最基础且最关键的 2-sat 性质：

对称性： 若 \(a\) 向 \(b\) 连边，则 \(b\) 的对面向 \(a\) 的对面连边。

假若我们要固定一个 bool 为 true 咋办（false 同理）：

即将命题转化为「若 \(a_3\) 为 false，则 \(a_3\) 为 true」（这样 \(a_3\) 只能为 true），注意此图仍然满足对称性。

缩点

没错，用 tarjan 将这个有向图缩点。

我们接下来证明：

此 2-sat 有解 \(\iff\) 不存在两个对面对的点处于同一个 SCC 中。

充分性

假设存在两个对面对的点处于同一个 SCC 中。那这个 bool 若为 true 则能推至 false，false 能推至 true，矛盾。

必要性

假设不存在两个对面对的点处于同一个 SCC 中且 2-sat 无解。

我们对于每一个 bool 构造：若 bool 的一个状态 \(x\) 能推到 \(y\)，则我们选择 \(y\) 状态，否则 \(x,y\) 无法互相推，随便选。

此时必然无解，假设是某一个 bool 的 \(x\) 推到了 \(y\)。但是由于我们的构造方案，得出 \(y\) 能够推到 \(x\)。这样发现 \(x,y\) 在同一个 SCC 中，矛盾。

构造

若判得有解，我们尝试构造一组解。

其实我们的构造方法就在上面的证明里。

我们用 tarjan 对 SCC 进行染色。由于tarjan 是逆拓扑序，所以我们每次在 bool 的两个状态中选颜色更小的即可。