Tarjan（年早失修 漏洞百出）

Tarjan是谁

Tarjan's SCCs（有向图强连通分量）algorithm

给定⼀个有向图 $G$，若存在 $rt\in V$，满⾜从 $rt$ 出发能到达 $V$ 中的所有的点，则称 $G$ 是⼀个源点为 $rt$ 流图。

从 $rt$ 出发做 $DFS$。

符号表

• $fa[x]$：$x$ 节点的父亲节点

• $anc[x]$：$x$ 节点的祖先点集

• $son[x]$：搜索树中 $x$ 节点的儿子节点集

• $e[x]$：$\{y \ | \ (x \to y)\in E\}$

• $dfn[x]$：$x$ 节点的时间戳

• $sbt[x]$：$x$ 节点为根的子树点集

• $low[x]$：$x$ 节点的追溯值

$G$ 中的每条有向边 $x\to y$ 必然是以下四种之⼀：

• 枝：$x=fa[y]$

• 前：$x\in (anc[y]-fa[y])$

• 后：$y\in (anc[x]-fa[x])$

• 横：$x\notin anc[y] \ \and \ y\notin anc[x]$ 此时一定满足 $dfn[x]>dfn[y]$

节点上的数字为时间戳：

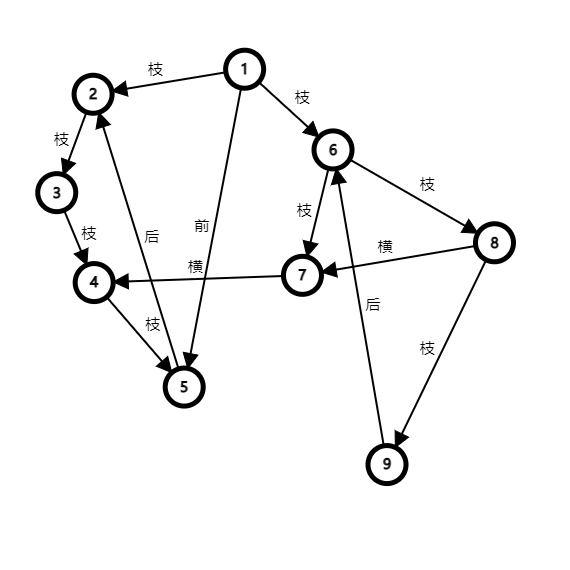
分析

我们在搜索树上分析，发现“前”边没有什么用处，因为搜索树上本来就存在从 $x$ 到 $y$ 的路径。“后”边非常有用，它可以和搜索树上从 $x$ 到 $y$ 的路径⼀起构成环。“横”边要看情况，如果从 $y$ 出发能找到⼀条路径回到 $x$ 的祖先节点，那么 $x\to y$ 就是有用的。

$low[x]$ 定义为满⾜以下条件的节点的最小时间戳：

• 该点在栈中。

• 存在⼀条从 $sbt[x]$ 出发的有向边，以该点为终点。

$tarjan(x)$ 主体

1. $low[x]=dfn[x]=++dfn\_time$

2. $for(y:e[x])\begin{cases}tarjan(y) \ check\_min(low[x],\color{blue}{low[y]}) & !vis[y] \\ check\_min(low[x],\color{red}{dfn[y]}) & y\in anc[x] \\ do \ nothing & otherwise\end{cases}$

3. $if(low[x]=dfn[x]) \ pop \ stack \ until \ x \ is \ popped \to a \ SCC$

注意标红和标蓝的不能改，不能错！！！

Code

P1407 [国家集训队]稳定婚姻

vector<int> e[N];
int dfn[N];//时间戳
int low[N];//追溯值
int tim=0;//时间戳计数器
int col[N];//所属 SCC （为其中一个点的 id）
int st[N];//stack
int tot=0;//stack_top
bool in[N];//是(1)否(0)在栈中
void tar(int x){
	dfn[x]=low[x]=++tim;//init
	st[++tot]=x;//进栈
	in[x]=1;
	for(int i:e[x]){
		if(!dfn[i]){//萌新
			tar(i);//递归
			ckmn(low[x],low[i]);
		}else if(in[i]){//祖先
			ckmn(low[x],dfn[i]);
		}
	}
	if(low[x]==dfn[x]){//导出 SCC
		do{
			col[st[tot]]=x;
                        //着上 x 的颜色，以后你就是 x 的人了
			in[st[tot]]=0;
		}while(st[tot--]!=x);//pop until x popped
	}
}

Tarjan's BCCs（无向图双连通分量）algorithm

与 SCC 类似，所以符号沿用

注意此时 $low[x]$ 的定义改变，且图 $G$ 中不再存在意义上的“横”边、“前”边。

$low[x]$ 定义为满⾜以下条件之一的节点的最小时间戳：

• 该点在 $sbt[x]$ 中。

• 存在⼀条从该点出发至 $sbt[x]$ 中任一点的非树边。

剩下的分析和算法就一样了~

桥

桥⼀定是搜索树上的边。

$$x\leftrightarrow fa[x] 为桥 \iff dfn[fa[x]]<low[x]$$

Code by FuZhenTao

const int SIZE=100010;
int head[SIZE],ver[SIZE*2],nxt[SIZE*2];
int dfn[SIZE],low[SIZE],n,m,tot,num;
bool bridge[SIZE*2];
void add(int x,int y){
 ver[++tot]=y;
 nxt[tot]=head[x];
 head[x]=tot;
}
void tarjan(int x,int in_edge){
 dfn[x]=low[x]=++num;
 for(int i=head[x];i;i=nxt[i]){
 int y=ver[i];
 if(!dfn[y]){
 tarjan(y,i);
 low[x]=min(low[x],low[y]);
 if(low[y]>dfn[x]) bridge[i]=bridge[i^1]=true;
 }
 else if(i!=(in_edge^1)){
 low[x]=min(low[x],dfn[y]);
 }
 }
}
int main(){
 cin>>n>>m;
 tot=1;
 for(int i=1;i<=m;i++){
 int x,y;
 cin>>x>>y;
 add(x,y);
 add(y,x);
 }
 for(int i=1;i<=n;i++){
 if(!dfn[i]) tarjan(i,0);
 }
 for(int i=2;i<tot;i+=2){
 if(bridge[i]) cout<<ver[i^1]<<" "<<ver[i]<<endl;
 }
}

割点

$$x 为割点 \iff \begin{cases}| \ son[x] \ |>1 & x=rt\\ \exists y\in son[x] \ , \ dfn[x]\leqslant low[y] & x\ne rt\end{cases}$$

Code by FuZhenTao

void tarjan(int x){
 dfn[x]=low[x]=++num;
 int flag=0;
 for(int i=head[x];i;i=nxt[i]){
 int y=ver[i];
 if(!dfn[y]){
 tarjan(y);
 low[x]=min(low[x],low[y]);
 if(low[y]>=dfn[x]){
 flag++;
 if(x!=root||flag>1) cut[x]=true;
 }
 }
 else low[x]=min(low[x],dfn[y]);
 }
}

e-DCC（边双连通分量）

设 $G$ 是无向连通图。

$$G 是 e-DCC \iff \kappa'(G)\geqslant2 \iff 任意⼀条边都包含在至少⼀个简单环中$$

只需要求出无向图中所有的桥，把桥都删除之后，图会分成若干个连通块，每个连通块就是⼀个"边双连通分量"。

Code by FuZhenTao

int c[SIZE],dcc;
void dfs(int x){
 c[x]=dcc;
 for(int i=head[x];i;i=nxt[i]){
 int y=ver[i];
 if(c[y]||bridge[i]) continue;
 dfs(y);
 }
}
for(int i=1;i<=n;i++){
 if(!c[i]){
 ++dcc;
 dfs(i);
 }
}

v-DCC（点双连通分量）

$$G 是 v-DCC \iff \kappa(G)\geqslant2 \iff n(G)\leqslant2 \or 任意两点都包含在至少⼀个简单环中$$

v-DCC 的求法炒鸡麻烦，鸽了。

由于 Tarjan $O(n)$ 求 LCA 好像并不是 Tarjan 的算法，而且倍增 $O(n\log n)$ 好用并好写，所以就不再论述了。