卷积：FFT&原根&NTT&MTT

半在线卷积 / 全在线卷积 / (semi-)relaxed convolution

后记

我想要说的前人们都说过了.jpg

EI - 脑力体操: 半在线卷积能做到多好? (van der Hoeven, 2007)

ScienceDirect - New algorithms for relaxed multiplication

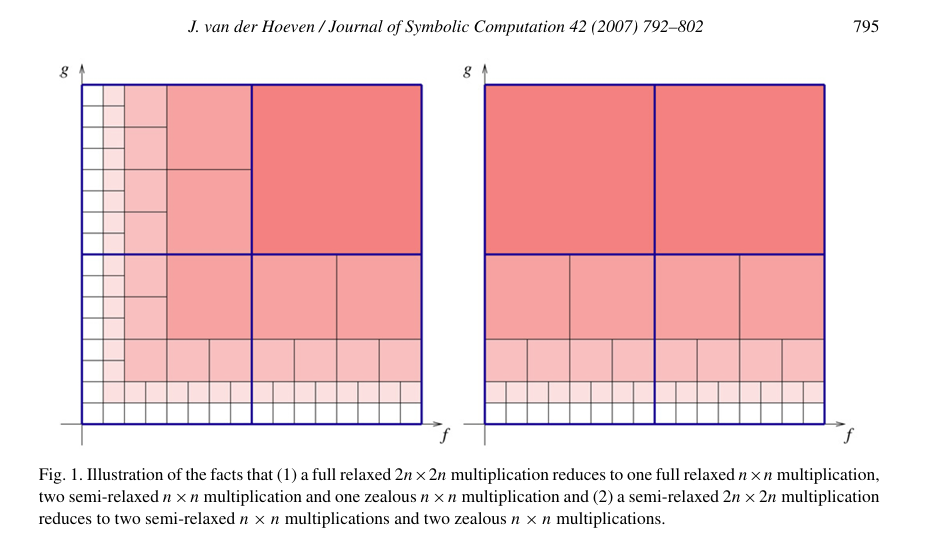
该文中最好的结果是 \(O\left( N\log N e^{\sqrt{2\log 2\cdot \log \log N}} \sqrt{\log \log N} \right)\)，我只知道全在线卷积和半在线卷积的最优复杂度一定相等(笑)。

发现这图和我之前做的动图非常相似，雷同了。从好的方面来说，我也是对上学者的脑电波了。

还有，其实 半在线卷积 和 全在线卷积 叫作 semi relaxed multiplication / full relaxed multiplication

---

卷积可视化的github仓库

半在线卷积

提前给出 \(g_0,\dots,g_{n-1}\)。对于 \(i=0\to(n-1)\)，依次给出 \(f_i\)，之后需立刻求出 \((fg)_i\)。

考虑 \(n\times n\) 二维平面上的网格，\((i,j)\) 格子上的值为 \(f_i\times g_j\)，则 \((fg)_i\) 为一条副对角线上值的和。

考虑对 \(f_x,\dots,f_{x+d-1}\) 与 \(g_y,\dots,g_{y+d-1}\) 做卷积，则结果可以表示为平面上左下角 \((x,y)\)，右上角 \((x+d-1,y+d-1)\) 的正方形。

接下来画的所有正方形不会有重叠。

我们可以画一个正方形当且仅当其在两维的投影区间我们均已知。

当所有 \(x+y=k\) 的位置 \((x,y)\) 均被方形覆盖，则 \((fg)_k\) 被求出。

所以我们只需要构造满足条件的方形划分即可。

复杂度 \(\text{src}(n)=n\log n+2\text{src}(n/2)\)，得 \(\text{src}(n)=O(n\log^2 n)\)。

半在线卷积：P4721 【模板】分治 FFT

全在线卷积

对于 \(i=0\to(n-1)\)，依次给出 \(f_i\) 和 \(g_i\)，之后需立刻求出 \((fg)_i\)。

与半在线卷积一样，构造方形划分即可。

如果你没懂这个动图：先解决一半大小的子问题，然后左上和右下同步做半在线卷积，最后右上角做离线卷积。

复杂度 \(\text{rc}(n)=\text{rc}(n/2)+2\text{src}(n)+n\log n\)，得 \(\text{rc}(n)=O(n\log^2 n)\)。

全在线卷积：qoj8721 括号序列

非递归

值得一提，通过上述可视化，很明显两者均可以将过程改为非递归。

半在线

全在线

2023年5月25日

之前写的 NTT 太丑了，改了一下

2022年7月22日

之前写的 NTT 太慢了，CF 题被卡常了，就改了一下

例题

P3803 【模板】多项式乘法（FFT）

record

FFT

bilibili 视频讲解

核心过程：

原根

Definition

若 \(a\) 模 \(m\) 的阶等于 \(\varphi(m)\)，则称 \(a\) 为模 \(m\) 的一个原根。\((a\in\mathbb{Z},m\in\mathbb{N^+})\)

Special Case

\(p=1004535809=2^{21}\times479+1,g=3\)

\(p=998244353=2^{23}\times7\times17+1,g=3 \leftarrow most \ important\)

\(p=469762049=2^{26}\times7+1,g=3\)

NTT

非常简单。

用原根代替FFT中的单位根，减小了常数、避免了精度误差而且方便好写。

适用条件：取模意义下求值且已知模数的原根。

MTT

如果NTT中模数的原根布吉岛且FFT中精度有问题，则MTT闪亮登场！

有如下几种：

P4245 【模板】任意模数多项式乘法 写了一个三模NTT

注意 MTT 是不好处理模意义下分数的，如 P3784 [SDOI2017] 遗忘的集合 这道题。

还有负数也不行（尤其是多项式乘法逆 \(2C-AC^2\)）如 P4239 任意模数多项式乘法逆 这道题。