分类讨论法

题目

平面上有九个整点，三点不共线，求证，必有三个点构成的三角形的重心是整点

solution

首先考虑十三个点的解法
首先设 $X_0,X_1,X_2$ 分别表示横坐标模 $3$ 同余于 $0,1,2$ 的点的集合，设 $Y_0,Y_1,Y_2$ 分别表示纵坐标模 $3$ 同余于 $0,1,2$ 的点的集合
由抽屉原理得 $\max(|X_0|,|X_1|,|X_2|)\geq5$ 设最大的集合为 $X'$
若 $\min(|X'\cap Y_0|,|X'\cap Y_1|,|X'\cap Y_2|)>0$ 则 $X'\cap Y_0,X'\cap Y_1,X'\cap Y_2$ 每个集合各任取一个元素作为三角形三个顶点即可
否则，设除一个空集以外剩余两个集合分别为 $Y',Y''$，由抽屉原理得 $\max(|Y'|,|Y''|)\geq3$ 从较大的集合中任取三个元素作为三角形三个顶点即可
原命题得证

观看此过程，发现有许多“浪费”的条件，所以尝试一下九个点

同样，设 $X_0,X_1,X_2$ 分别表示横坐标模 $3$ 同余于 $0,1,2$ 的点的集合，设 $Y_0,Y_1,Y_2$ 分别表示纵坐标模 $3$ 同余于 $0,1,2$ 的点的集合
设:

$$A=\begin{pmatrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{pmatrix}=\begin{pmatrix}|X_0\cap Y_0|&|X_0\cap Y_1|&|X_0\cap Y_2|\\|X_1\cap Y_0|&|X_1\cap Y_1|&|X_1\cap Y_2|\\|X_2\cap Y_0|&|X_2\cap Y_1|&|X_2\cap Y_2|\end{pmatrix}$$

发现，若满足其中之一：

• $a_{i,1}>0$ 且 $a_{i,2}>0$ 且 $a_{i,3}>0$ ①
• $a_{1,i}>0$ 且 $a_{2,i}>0$ 且 $a_{3,i}>0$ ②
• $a_{1,p_1}>0$ 且 $a_{2,p_2}>0$ 且 $a_{3,p_3}>0$，其中 $p_1,p_2,p_3$ 是 $3$ 的一个排列 ③
• $a_{i,j}\geq3$ ④

则满足必有三个点构成的三角形的重心是整点
现在只要说明不存在九个整点不满足其中任意一个即可
由于要使④不成立，则必有 $5$ 个 $A$ 中元素不为零（抽屉原理）
由于 $A$ 中每一行，每一列都是轮换对称的，不妨设 $a_{2,2}>0$
再分两种情况：（以下图中红框为大于零，蓝框为零，橙色、紫色框中至少有一个为零，绿线两头至少有一个为零）
1. 有一个角上不为零
由于 $A$ 是旋转对称的，不妨设 $a_{1,1}>0$
此时 $a_{3,3}=0$（不然就满足③了）

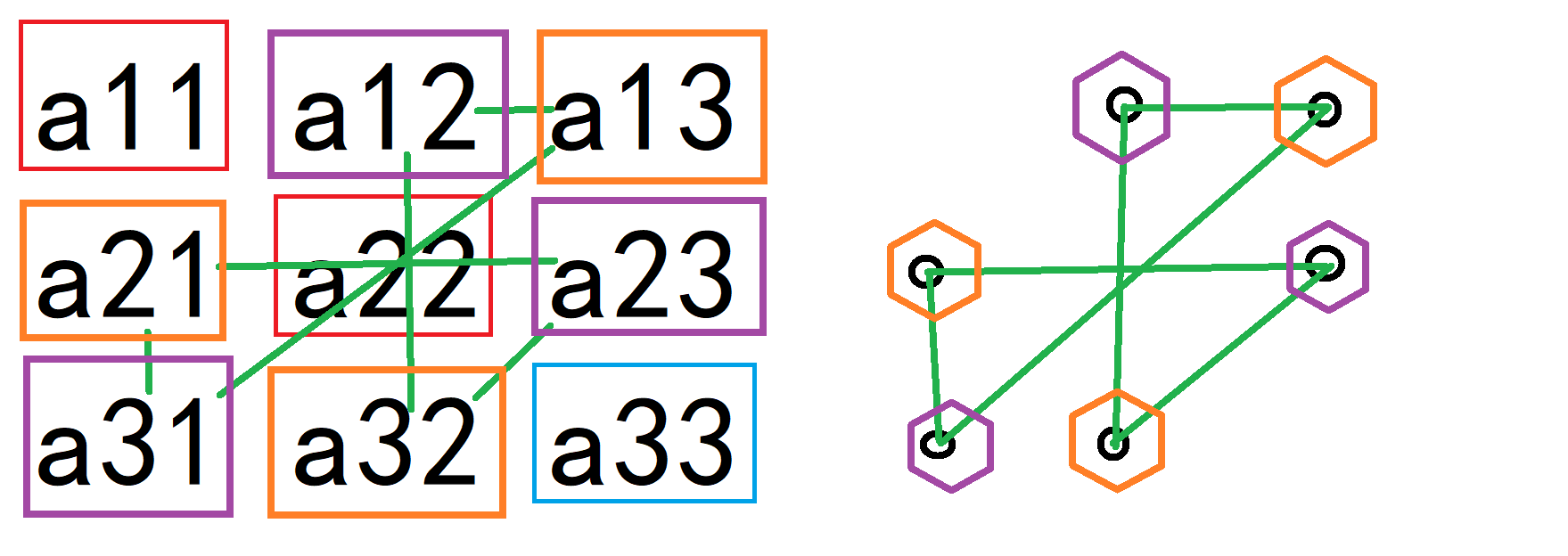
经枚举，不存在
2. 有一个棱上不为零
由于 $A$ 是旋转对称的，不妨设 $a_{2,1}>0$
此时 $a_{2,3}=0$（不然就满足①了）

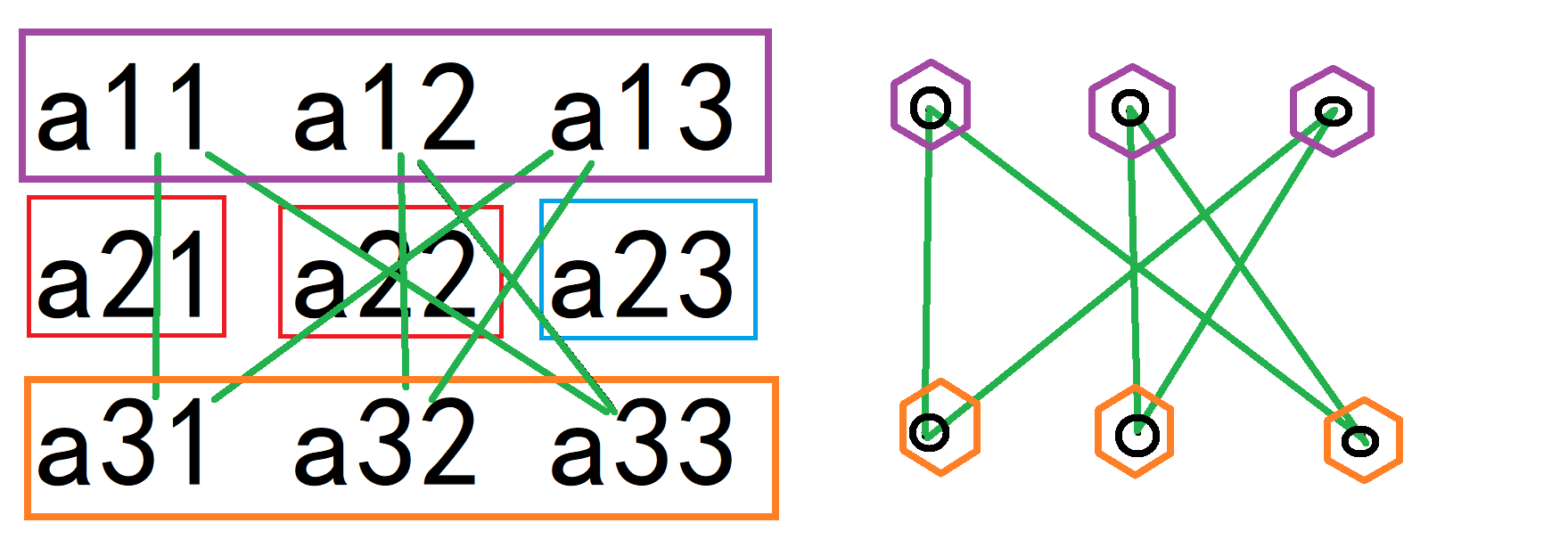
经枚举，不存在

综上，必有三个点构成的三角形的重心是整点，原命题得证