重修 Dp 总览

Konata28

三层：阶段，状态，决策。

写在程序里大概是这样的：

For(阶段){
	For(状态){
		1.决策
		2.For(决策集合) 决策
	}
}

阶段

Forward

对，就这一个词。为了满足无后效性必须让阶段只能向前。

只能向前的：时间，单向火车等。

经典的阶段：UVA1025 城市里的间谍 A Spy in the Metro

决策

先考虑这个，再说状态。

考虑在一个情景下，如何转移。或者说，如何将题目中的条件写成公式。

状态

构建满足决策和时间复杂度的状态。

注意：一道题可能有不同的解法对应不同的状态定义，但只有部分的时间复杂度是对的。

经典的状态定义不同：UVA10934 装满水的气球 Dropping water balloons

Hu Kang

以下均以 01 背包举例。

状态表示

将每一个状态看作一个集合集的属性。

$f[i,j]$ 表示前 $i$ 个物品中总体积为 $j$ 的物品集合集的元素大小和的最大值（属性）。

$e.g.$

$$id:1,2,3$$

$$w_i:4,5,9$$

$$v_i:6,8,7$$

$$f[3,9]\to\{\{1,2\},\{3\}\}$$

其中 $\{1,2\}$ 的价值和最大，为 $6+8=14$，故 $f[3,9]=14$

常见的属性有：大小、最值、和、乘积、异或和……

状态转移

对集合集中集合的划分。

将 $f[i,j]$ 的集合集划分成包含 $i$ 物品的集合和不包含 $i$ 物品的集合。

两种情况分别对应 $f[i-1,j]$ 和 $f[i-1,j-w_i]+v_i$。

所以状态转移方程为 $f[i,j]=\max(f[i-1,j],f[i-1,j-w_i]+v_i)$。

$e.g.$

$$id:1,2,3,4$$

$$w_i:4,5,9,8$$

$$v_i:6,8,7,1$$

$$f[4,13]\to\{\color{blue}{\{1,3\}},\color{red}{\{2,4\}}\}$$

蓝色为不含 $i$ 的，红色为含 $i$ 的。

再思考，可以用滚动数组优化空间复杂度。

Unknown

拿到一道题，先写出状态转移方程，再优化时间复杂度。

状态优化

对于状态可累加
$e.g.dp[i+j]=dp[i]+dp[j]+i+j$
的，用倍增优化

决策优化：

单调队列优化

$e.g.dp[i][j]=\max(dp[i-1][j-233]+(j-233)^2,dp[i-1][j-232]+(j-232)^2,...,dp[i-1][j]+j^2)$

斜率优化

$e.g.dp[i]=\max(dp[1]+i,dp[2]+2i,...,dp[i-1]+(i-1)i)$

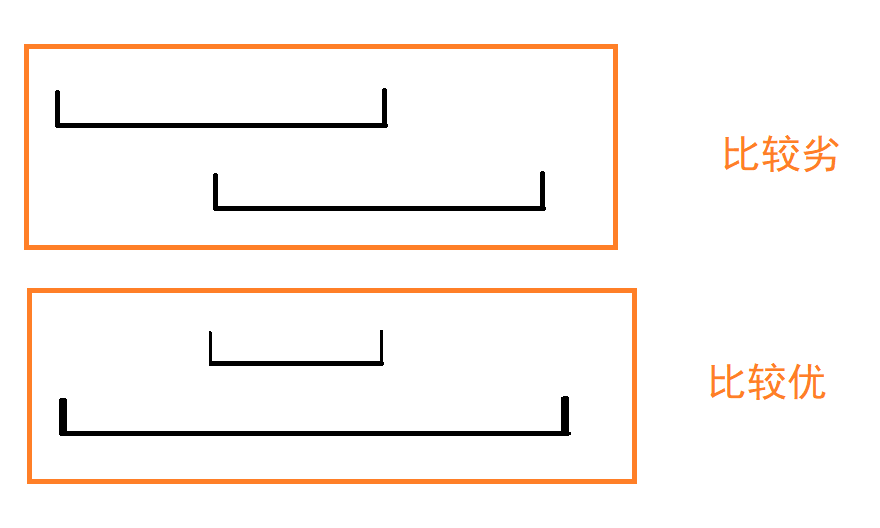
四边形不等式优化

交叉小于包含
$e.g.dp[i][j]=\max(dp[i][i]+dp[i+1][j],dp[i][i+1]+dp[i+2][j],...,dp[i][j-1]+dp[j-1][j],dp[i][j]+dp[j][j])$