二维问题怎么转化？

先将二维问题转为一维问题，再用低复杂度解决另一维

题目
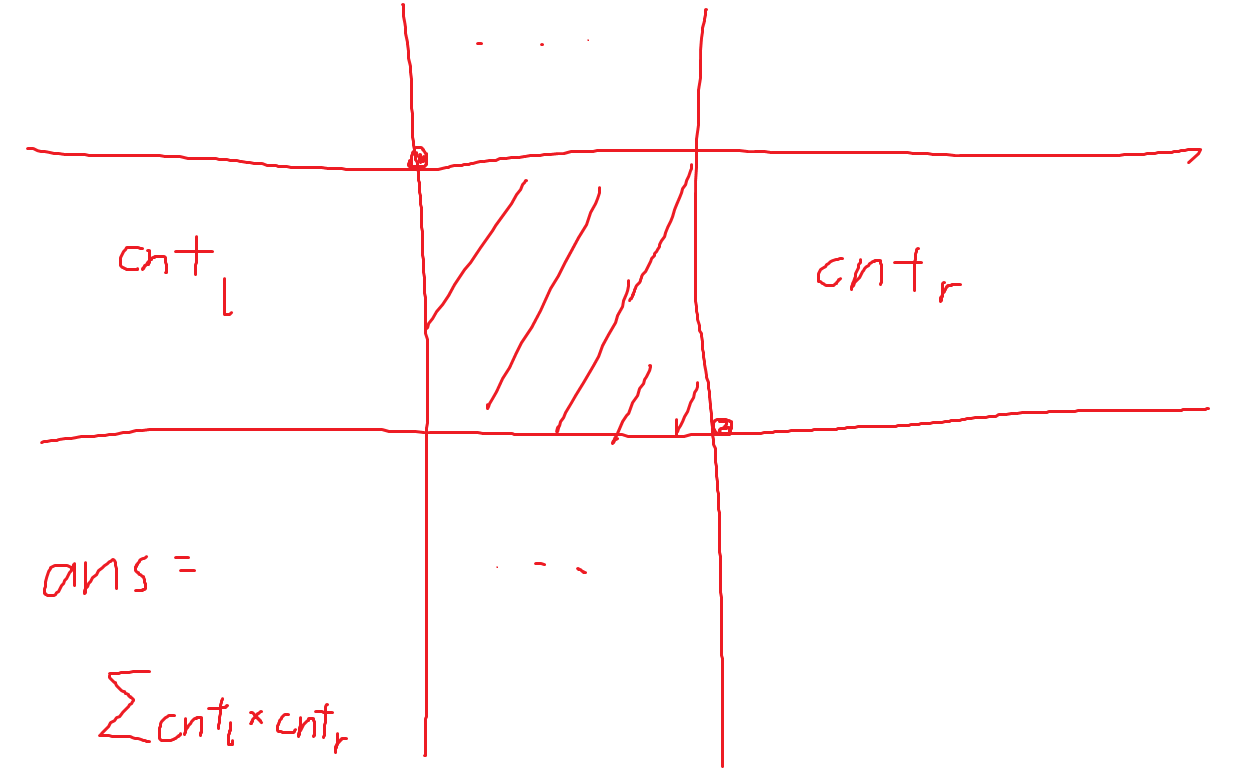
先离散化,再\(\mathcal{O}(n^2)\)枚举两个点,横着划两刀,代表上下边界
再数左右侧点的个数（预处理二维前缀和）,相乘后每种相加即可

ACcode:

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define pi pair<int,int>
#define X first
#define Y second
#define mkp make_pair
#define fo(x,y,z) for(int x=y;x<=z;x++)
#define N 2600
using namespace std;
typedef long long ll;
void setio(string);

int pre[N][N],mp[N][N]; 
int n;
pi pos[N];
int xxx[N],yyy[N]; 
ll ans;
int sum(int x1,int y1,int x2,int y2){
	return pre[x2][y2]-pre[x1-1][y2]-pre[x2][y1-1]+pre[x1-1][y1-1]+1;
}
int main(){
	setio("");
	cin>>n;
	fo(i,1,n){
		cin>>pos[i].X>>pos[i].Y;
		xxx[i]=pos[i].X;
		yyy[i]=pos[i].Y;
	}
	sort(xxx+1,xxx+1+n);
	sort(yyy+1,yyy+1+n);
	fo(i,1,n){
		pos[i].X=lower_bound(xxx+1,xxx+1+n,pos[i].X)-xxx;
		pos[i].Y=lower_bound(yyy+1,yyy+1+n,pos[i].Y)-yyy;
	}
	fo(i,1,n){
		mp[pos[i].X][pos[i].Y]=1;
	}
	fo(i,1,n){
		fo(j,1,n){
			pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1];
			if(mp[i][j])pre[i][j]++;
		}
	} 
	ans=1+n;
	fo(i,1,n-1){
		fo(j,i+1,n){
			ans+=sum(1,min(pos[i].Y,pos[j].Y),min(pos[i].X,pos[j].X)-1,max(pos[i].Y,pos[j].Y))
				*sum(max(pos[i].X,pos[j].X)+1,min(pos[i].Y,pos[j].Y),n,max(pos[i].Y,pos[j].Y));
		}
	}
	cout<<ans<<endl;
	return 0;
}
void setio(string name){
	ios_base::sync_with_stdio(0);
	cin.tie(0);
    if(name!=""){
        freopen((name+".in").c_str(),"r",stdin);
        freopen((name+".out").c_str(),"w",stdout);
    }
}