关于简单的莫队
莫队
简介
莫队算法可以解决一类离线区间询问问题,适用性极为广泛。同时将其加以扩展,便能轻松处理树上路径询问以及支持修改操作。
形式
假设 \(n=m\),那么对于序列上的区间询问问题,如果从 \([l,r]\) 的答案能够 \(O(1)\) 扩展到 \([l-1,r],[l+1,r],[l,r+1],[l,r-1]\)(即与 \([l,r]\) 相邻的区间)的答案,那么可以在 \(O(n\sqrt{n})\) 的复杂度内求出所有询问的答案。
解释
离线后排序,顺序处理每个询问,暴力从上一个区间的答案转移到下一个区间答案(一步一步移动即可)。
排序方法
对于区间 \([l,r]\), 以 \(l\) 所在块的编号为第一关键字,\(r\) 为第二关键字从小到大排序。
例题
小B 有一个长为 \(n\) 的整数序列 \(a\),值域为 \([1,k]\)。
他一共有 \(m\) 个询问,每个询问给定一个区间 \([l,r]\),求:
其中 \(c_i\) 表示数字 \(i\) 在 \([l,r]\) 中的出现次数。
对于 \(100\%\) 的数据,\(1\le n,m,k \le 5\times 10^4\)。
先按上述的方法排序,对于每次对 \(c_i\) 的更新,贡献为 \(\pm 2c_i+1\),直接维护即可。
#include <bits/stdc++.h>
using namespace std;
#define N 50005
int n,m,k,a[N],cnt[N],ans[N];
struct node
{
int l,r,id;
}q[N];
int cmp(node x,node y)
{
if(x.l/250==y.l/250)
return x.r<y.r;
return x.l/250<y.l/250;
}
int main( void )
{
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
int l=1,r=0,now=0;
for(int i=1;i<=m;i++)
{
for(int j=l;j<q[i].l;j++)
{
now+=cnt[a[j]]*-2+1;
cnt[a[j]]--;
}
for(int j=q[i].l;j<l;j++)
{
now+=cnt[a[j]]*2+1;
cnt[a[j]]++;
}
for(int j=q[i].r+1;j<=r;j++)
{
now+=cnt[a[j]]*-2+1;
cnt[a[j]]--;
}
for(int j=r+1;j<=q[i].r;j++)
{
now+=cnt[a[j]]*2+1;
cnt[a[j]]++;
}
l=q[i].l;
r=q[i].r;
ans[q[i].id]=now;
}
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
回滚莫队
简介
有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在 \(O(n \sqrt m)\) 的时间内解决问题。
形式
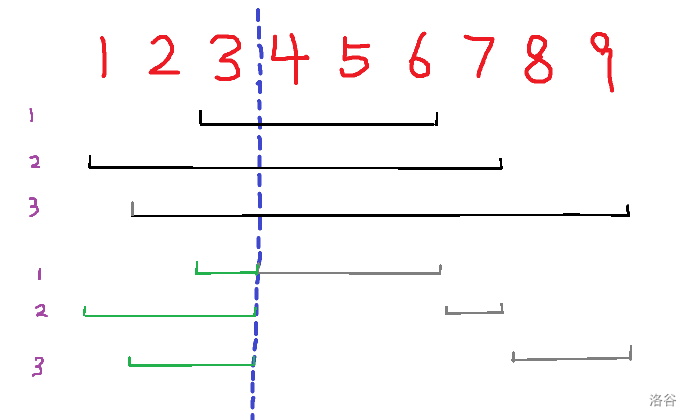
第一步还是将询问的区间按左端点所在块分组,每组内按右端点排序。
实现时对每组单独处理,以左端点所在块右端点(蓝色虚线)为界线。
- 若左右区间在同一块内,直接暴力计算。
- 在界线右边的区间(灰色线)的右端点单调不降,可以顺着遍历每个位置。
- 在界限左边的区间(绿色线)的左端点无序,每次都需要重新遍历,答案在右边的基础上贡献。
复杂度证明
设分块大小为 \(b\):
- 对于左右区间在同一块内的询问,每次计算复杂度 \(O(b)\);
- 对于界线左边的区间,每次只会在左端点所在块内计算,复杂度 \(O(b)\);
- 对于界限右边的区间,在每一组内顺着遍历,最多 \(n\) 次,而有 \(\frac{n}{d}\) 组。
总复杂度为 \(O(mb+\frac{n^2}{d})\),\(b=\frac{n}{\sqrt{m}}\) 时最优,为 \(O(n\sqrt{m})\)。
例题
不删除莫队
给定一个序列,多次询问一段区间 \([l,r]\),求区间中相同的数的最远间隔距离。
序列中两个元素的间隔距离指的是两个元素下标差的绝对值。
对于 \(40\%\) 的数据,满足 \(1\leq a_i \leq 400\),\(1\leq n,m\leq 60000\)。
对于 \(100\%\) 的数据,满足 \(1\leq n,m\leq 2\cdot 10^5\),\(1\leq a_i\leq 2\cdot 10^9\)。
按上述方法实现就行,详细请看代码注释。
#include <bits/stdc++.h>
using namespace std;
#define N 200005
int n,m,q,a[N],tot,top,ans[N];
//一个块的左端点、右端点和某点所在块
int l[505],r[505],to[N];
//界线右边区间对应数的最小、最大下标 和界线左边区间对应数的最小、最大下标
int l1[N],r1[N],l2[N],r2[N];
//当前界限右边的答案和总区间的答案
int now;
pair<int,int> p[N];
struct node
{
int l,r,id;
}st[N];
vector<node>b[505];
//求l、r和to
void init()
{
m=sqrt(n);
for(int i=1;i<=m;i++)
{
l[i]=r[i-1]+1;
r[i]=l[i]+m-1;
}
if(r[m]<n)
{
m++;
l[m]=r[m-1]+1;
r[m]=n;
}
for(int i=1;i<=m;i++)
for(int j=l[i];j<=r[i];j++)
to[j]=i;
}
bool cmp(node i,node j)
{
return i.r<j.r;
}
int main( void )
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
p[i]={a[i],i};
}
//离散化
sort(p+1,p+1+n);
for(int i=1;i<=n;i++)
{
if(p[i].first!=p[i-1].first)
tot++;
a[p[i].second]=tot;
}
init();
scanf("%d",&q);
for(int i=1;i<=q;i++)
{
int x,y;
scanf("%d%d",&x,&y);
b[to[x]].push_back({x,y,i});
}
for(int i=1;i<=m;i++)
sort(b[i].begin(),b[i].end(),cmp);
//如果像普通莫队那样直接遍历整个q每次都需要判断是否在新的组内,比较麻烦
//可为每组开一个vector,对其分开计算
for(int i=1;i<=m;i++)
{
int len=b[i].size();
if(!len)
continue;
//这里的l1得赋较大值,否则后面求min(l1,l2)时会算错
memset(l1,0x3f,sizeof(l1));
memset(r1,0,sizeof(r1));
int x=r[to[b[i][0].l]]+1,y=x-1;
now=0;
for(int j=0;j<len;j++)
{
//在同一块内暴力算
if(to[b[i][j].l]==to[b[i][j].r])
{
for(int k=b[i][j].l;k<=b[i][j].r;k++)
{
if(!l2[a[k]])
l2[a[k]]=k;
r2[a[k]]=k;
ans[b[i][j].id]=max(ans[b[i][j].id],r2[a[k]]-l2[a[k]]);
}
//复原时不能memset
for(int k=b[i][j].l;k<=b[i][j].r;k++)
l2[a[k]]=r2[a[k]]=0;
continue;
}
//算界线右边的
for(int k=y+1;k<=b[i][j].r;k++)
{
if(l1[a[k]]==l1[0])
l1[a[k]]=k;
r1[a[k]]=k;
now=max(now,r1[a[k]]-l1[a[k]]);
}
ans[b[i][j].id]=now;
top=0;
//算界线左边的
for(int k=x-1;k>=b[i][j].l;k--)
{
l2[a[k]]=k;
if(!r2[a[k]])
r2[a[k]]=k;
ans[b[i][j].id]=max(ans[b[i][j].id],max(r1[a[k]],r2[a[k]])-min(l1[a[k]],l2[a[k]]));
}
//复原
for(int k=x-1;k>=b[i][j].l;k--)
l2[a[k]]=r2[a[k]]=0;
//右指针向右跳
y=b[i][j].r;
}
}
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
return 0;
}
不增加莫队
有一个长度为 \(n\) 的数组 \(\{a_1,a_2,\ldots,a_n\}\)。
\(m\) 次询问,每次询问一个区间内最小没有出现过的自然数。
对于 \(30\%\) 的数据:\(1\leq n,m\leq 1000\)。
对于 \(100\%\) 的数据:\(1\leq n,m\leq 2\times {10}^5\),\(1\leq l\leq r\leq n\),\(0\leq a_i\leq 2\times 10^5\)。
一个集合内最小没有出现过的自然数通常被称为mex。
如果连续插入数,难以维护mex。
容易发现,如果已知mex与一个集合,每次删除其中的数,则mex的变化只会有两种可能:
- 若当前要删的数 \(x\) 只剩一个,并且 \(x<mex\),则删后 \(mex\) 变为 \(x\);
- 否则,\(mex\) 不变。
因此也可以用回滚莫队实现,对于每一组内按右端点降序排序,先求出其左侧所在块的左端点到最大右端点的mex,再考虑每次删去一个数时能否更新的mex。
#include <bits/stdc++.h>
using namespace std;
int n,m,q,a[200005],l[505],r[505],to[200005],flag1[200005],flag2[200005],now,ans[200005];
struct node
{
int l,r,id;
}b[200005];
void init()
{
m=sqrt(n);
for(int i=1;i<=m;i++)
{
l[i]=r[i-1]+1;
r[i]=l[i]+m-1;
}
if(r[m]<n)
{
m++;
l[m]=r[m-1]+1;
r[m]=n;
}
for(int i=1;i<=m;i++)
for(int j=l[i];j<=r[i];j++)
to[j]=i;
}
bool cmp(node i,node j)
{
if(to[i.l]==to[j.l])
return i.r>j.r;
return to[i.l]<to[j.l];
}
int main( void )
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=q;i++)
{
scanf("%d%d",&b[i].l,&b[i].r);
b[i].id=i;
}
init();
sort(b+1,b+1+q,cmp);
int x=0,y=0;
//这里也可以用上一题的写法,懒得改了QwQ
for(int i=1;i<=q;i++)
{
//在同一块内暴力算
if(to[b[i].l]==to[b[i].r])
{
for(int j=b[i].l;j<=b[i].r;j++)
flag2[a[j]]=1;
ans[b[i].id]=n;
if(!flag2[0])
ans[b[i].id]=0;
for(int j=b[i].l;j<=b[i].r;j++)
if(!flag2[a[j]+1])
ans[b[i].id]=min(ans[b[i].id],a[j]+1);
//复原
for(int j=b[i].l;j<=b[i].r;j++)
flag2[a[j]]=0;
continue;
}
//如果这次询问和上次不在一组
if(to[b[i].l]!=to[x])
{
for(int j=l[to[x]];j<=y;j++)
flag1[a[j]]=0;
now=n;
for(int j=l[to[b[i].l]];j<=b[i].r;j++)
flag1[a[j]]++;
//暴力算mex
for(int j=0;j<n;j++)
if(!flag1[j])
{
now=j;
break;
}
x=b[i].l;
y=b[i].r;
}
//减右边的
for(int j=y;j>b[i].r;j--)
{
flag1[a[j]]--;
if(!flag1[a[j]])
now=min(now,a[j]);
}
ans[b[i].id]=now;
//减左边的
for(int j=l[to[b[i].l]];j<b[i].l;j++)
{
flag1[a[j]]--;
if(!flag1[a[j]])
ans[b[i].id]=min(ans[b[i].id],a[j]);
}
//复原
for(int j=l[to[b[i].l]];j<b[i].l;j++)
flag1[a[j]]++;
x=b[i].l;
y=b[i].r;
}
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号